Релятивистік динамика туралы ұғым.
Салыстырмалы принцип тұрғысынан физиканың кез келген заңының математикалық формасы барлық инерциалды санақ жүйесінде инвариантты болуы шарт. Бұл К 'жүйесіндегі кез келген физикалық құбылысты К жүйесінде сипаттайтын теңдеуден штрихталмаған шамаларды штрихталған шамалармен қарапайым алмастыру жолымен алуға болады. Келтірілген шартты физикалық заңдардың Лоренц түрлендіруіне қатысты инварианттылық шарты деп атайды.
Ньютон классикалық механикасының материалдық нүкте үшін негізгі заңы:
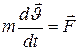 немесе
немесе 
мұндағы нүктенің массасы m барлық инерциалдық есептеу жүйесінде тұрақты, ал Лоренц түрлендіруіне қатысты инвариантсыз (тұрақты емес) болады. Сондықтан бұл заң релятивистік механиканың негізгі заңы бола алмайды.
Салыстырмалылықтың арнаулы теориясында дененің массасы m инерциалды есептеу жүйесіне қатысты жылдамдығы  тәуелді.
тәуелді.
 (1)
(1)
Мұндағы m0 – қарастырып отырған дененің жылдамдығы  болған кездегі, яғни дене тыныштықта тұрған кездегі инерциалды санақ жүйесінде өлшенген массасы. Оны тыныштық масса, ал
болған кездегі, яғни дене тыныштықта тұрған кездегі инерциалды санақ жүйесінде өлшенген массасы. Оны тыныштық масса, ал 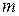 - қозғалыстағы дененің массасы, яғни релятивистік масса деп атайды. Яғни
- қозғалыстағы дененің массасы, яғни релятивистік масса деп атайды. Яғни  тәуелділігнің сызбасы арқылы талдауға болады. Массалар
тәуелділігнің сызбасы арқылы талдауға болады. Массалар  қатынасының мәні бір-бірінен
қатынасының мәні бір-бірінен  жылдамдықта ғана бірден айтарлықтай ауытқиды. Егер
жылдамдықта ғана бірден айтарлықтай ауытқиды. Егер 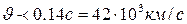 болса, онда
болса, онда  жуықтап 1% артық болады. Жоғарыдағы (1) өрнегі элементар бөлшектер: электрондар, протондар,
жуықтап 1% артық болады. Жоғарыдағы (1) өрнегі элементар бөлшектер: электрондар, протондар, 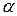 -бөлшектер арқылы жасалған тәжірибелерде толық орындалатындығын көрсетті.
-бөлшектер арқылы жасалған тәжірибелерде толық орындалатындығын көрсетті.
Жоғарыдағы (1) теңдеуін релятивистік механикада импульстің сақталу заңы орындалады деп алып, шығарып алуға болады.
Тұйық жүйеде өтетін кез келген процестерде оның импульсі (жүйені түзейтін барлық бөлшектердің релятивистік массаларының жылдамдықтарына көбейтіндісінің геометриялық қосындысы) өзгермейді.
Релятивистік динамиканың негізгі теңдеуін
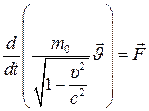 немесе
немесе 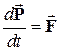 (2)
(2)
мұндағы
 (3)
(3)
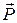 - релятивистік механикадағы дене (материалдық нүкте) импульсі.
- релятивистік механикадағы дене (материалдық нүкте) импульсі.
Егер бір инерциалды санақ жүйеден басқа инерциалды санақ жүйесіне өткен кезде күш құраушыларын координата осьтерінің түлендіруі белгілі заңдылық бойынша жүретін болса, онда (2) теңдеуі Лоренц инварианттылық шартын қанағаттандыратындығын дәлелдеуге болады.
Төменгі жылдамдық кезінде (  ) дене массасы
) дене массасы 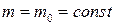 , релятивистік механиканың динамика теңдеуі классикалық механиканың Ньютон теңдеуімен дәл келеді. Дененің импульсі
, релятивистік механиканың динамика теңдеуі классикалық механиканың Ньютон теңдеуімен дәл келеді. Дененің импульсі
 (4)
(4)
жылдамдықтың сызықтық функциясы болады.
Барлық денелерде тыныштықтағы масса  үлкен, сондықтан (1), (3) дененің релятивистік массасы мен импульсі жылдамдық
үлкен, сондықтан (1), (3) дененің релятивистік массасы мен импульсі жылдамдық  ұмтылғанда шексіз өсе бермейді. Барлық нақты күштер – шектеулі: олардың денегі әсері уақытқа байланысты шексіз емес. Олар денеге шексіз импульс бере бермейді. Сондықтан дененің жылдамдығы кез келген инерциалдық санақ жүйесіне қатысты вакуумдағы жарық жылдамдығына теңесе алмайды. Ол әрқашанда жарық жылдамдығынан кіші болады. Бұл жасалған қорытынды тыныштықтағы массалары 0-ге тең болатын, фотон, нейтрино, антинейтринодан басқа, атомдар, молекулалармен элементар бөлшектер үшін орындалады.
ұмтылғанда шексіз өсе бермейді. Барлық нақты күштер – шектеулі: олардың денегі әсері уақытқа байланысты шексіз емес. Олар денеге шексіз импульс бере бермейді. Сондықтан дененің жылдамдығы кез келген инерциалдық санақ жүйесіне қатысты вакуумдағы жарық жылдамдығына теңесе алмайды. Ол әрқашанда жарық жылдамдығынан кіші болады. Бұл жасалған қорытынды тыныштықтағы массалары 0-ге тең болатын, фотон, нейтрино, антинейтринодан басқа, атомдар, молекулалармен элементар бөлшектер үшін орындалады.
Енді релятивистік механикадағы материалдық нүктенің кинетикалық энергиясын анықтайық. Материалдық нүктенің кинетикалық энергиясы элементар F күшінің әсерінен, орын ауыстыруға dr жұмсалған жұмысына тең:
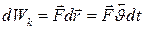 (5)
(5)
мұндағы  -нүкте жылдамдығы. Сонда (2) теңдеуінен
-нүкте жылдамдығы. Сонда (2) теңдеуінен
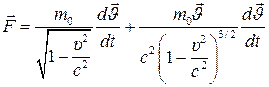
сондықтан

өйткені 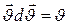 және
және 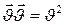 , онда
, онда
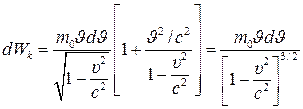
Масса өсімшесін
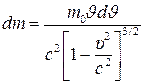
Сонымен материалдық нүктенің жылдамдығы өзгерген кезде оның кинетикалық энергиясы мен релятивистік массалары бір-біріне тура пропорционал
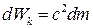 (6)
(6)
Тыныштықтағы дененің жылдамдығы 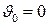 , ал релятивистік массасы
, ал релятивистік массасы 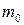 болады. Олай болса, (6) теңдеуін
болады. Олай болса, (6) теңдеуін 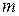 бойынша
бойынша 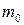 -дан
-дан 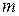 -ге дейін интегралдап, материалдық нүктенің кинетикалық энергиясын анықтайық:
-ге дейін интегралдап, материалдық нүктенің кинетикалық энергиясын анықтайық:
 (7)
(7)
Осы өрнекке Тейлор қатарына жіктеп

Егер 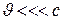 болса, қатардың алғашқы екі мүшесімен шектеледі:
болса, қатардың алғашқы екі мүшесімен шектеледі:
 (8)
(8)
Төменгі жылдамдықта материалдық нүктенің кинетикалық энергиясы релятивистік (8) өрнек арқылы есептеледі. Ол Ньютон механикасындағы материалдық нүктенің кинетикклық энеригясына сәйкес келеді. Ал үлкен жылдамдықта материалдық нүктенің кинетикалық энергиясы  , ол
, ол  немесе
немесе 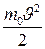 сәйкес келмейді.
сәйкес келмейді.
Релятивистік бөлшектің толық энергиясы (масса мен энергияның өзарабайланыс заңы)

Әр түрлі санақ жүйесіндегі толық энергия әр түрлі болады. Тұйық жүйенің толық энергиясы  тұрақты. Ол уақыт өзгерісіне байланысты өзгермейді. Бұл уақыттың біртектілігінің салдары болып табылады. Барлық инерциалды санақ жүйесіндегі дененің энергиясы мен импульсінің арасындағы байланыс
тұрақты. Ол уақыт өзгерісіне байланысты өзгермейді. Бұл уақыттың біртектілігінің салдары болып табылады. Барлық инерциалды санақ жүйесіндегі дененің энергиясы мен импульсінің арасындағы байланыс


Бөлшектің барлық инерциалдық санақ жүйесіндегі энергиясы мен импульсінің арасындағы релятивистік қатынас
 (9)
(9)
Ол
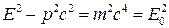
Енді (2) теңдеуді 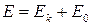 қойып
қойып
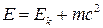
Импульске қатысты шешетін болсақ,
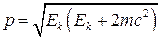
Немесе релятивистік бөлшектің энергиясы мен импульсінің арасындағы байланыс энергиясын өрнектейтін формула
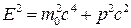
Дата добавления: 2016-02-24; просмотров: 8241;
