ИЗМЕРЕНИЕ РАССТОЯНИЙ

Измерения форм сейчас становятся все более важными в географическом анализе, в частности, благодаря растущему пониманию связей между формами и функциями ландшафтов. В то же время, существует устоявшийся интерес к измерению расстояний. Измерение расстояний между объектами важно не только для дальнейшего анализа отношений между ними, но и как непосредственная оценка движения к ним, от них и вокруг них. Как вы увидите, расстояние может измеряться довольно просто - как физическое расстояние между двумя точками. Но кроме того, измерение расстояния может учитывать стоимость продвижения по пересеченной местности или по дорожной сети в противоположность движения напрямую, или в обход барьеров, которые препятствуют движению. Эти меры называются функциональными расстояниями (functional distance).

Простое расстояние

Как мы уже видели, определение простого расстояния, известного также как эвклидово расстояние, относительно просто и в растровых, и в векторных ГИС. В растровых системах расстояние измеряется количеством ячеек между точками, которое может преобразовываться в стандартные единицы умножением на величину разрешения растра. Расстояния по диагонали определяются по теореме Пифагора. Кроме такого способа определения расстояния между точками существует и другой, при котором заранее просчитываются расстояния от определенной точки до всех других возможных точек покрытия. В растре это делается созданием набора концентрических окружностей с центром в заданной точке, каждая последующая из которых имеет радиус на одну ячейку больше. В результате образуетсяизотропная поверхность (isotropic surface), поскольку она одинакова по всем направлениям (Рисунок 8.4а). В трехмерном пространстве она может изображаться как конус, центр основания которого находится в выбранной точке. Карта изотропной поверхности является по сути картой путешествий из заданной точки ко всем другим объектам базы данных. Такая карта имеет тот же эффект, что и полная карта дорог, показывающая расстояния путешествия по всем направлениям от заданной начальной точки. Ее преимущество очевидно, когда нам требуется выполнить множество измерений расстояния от одной точки, — они уже содержатся в изотропной поверхности. В дальнейшем мы увидим, как мы должны модифицировать изотропную поверхность для учета различий на поверхности и существования барьеров.

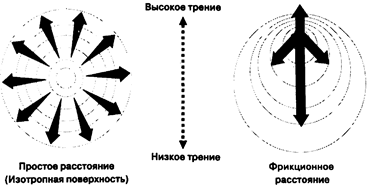
Рисунок 8.4. Простое и функциональное расстояния, а) Отсчет простого расстояния от центральной точки создает изотропную поверхность. b) Изменение изотропной поверхности из-за сопротивления при передвижении.

Есть также вариант этого метода, в котором расстояния отмеряются не от точки, а от полигона. Например, это могут быть расстояния от границы города. В результате мы опять имеем карту путешествий ко всем точкам покрытия вне города от его границы.

Как уже говорилось, в векторном покрытии расстояние между двумя точками определяется по теореме Пифагора, а общей длиной многосегментной линии является сумма длин составляющих ее отрезков. Поскольку векторные структуры данных не определяют явным образом содержимое пространства в промежутках между введенными объектами, в этих промежутках не могут выполняться и расчеты.

Указанное ограничение также относится и к созданию изотропных поверхностей. Для выполнения таких расчетов требуется другая структура векторных данных, специально созданная для моделирования поверхностей. Наиболее распространенной такой структурой является упомянутая в Главе 4нерегулярная триангуляционная сеть (TIN), которую мы рассмотрим более подробно в Главе 10. В этой модели могут определяться расстояния, но со значительными вычислительными затратами. Пользователи ГИС, работающие с моделями поверхностей, чаще всего полагаются на растровые системы, особенно тогда, когда требуется измерять расстояния на поверхностях.