Меры формы полигонов
Как мы видели, имеются два основных аспекта измерения формы полигонов. Первый, на основе идеи перфорированных и фрагментированных регионов, имеет общее названиепространственной целостности (spatial integrity). Вторая мера, - на основе идеи конфигурации границы, — более близкая к нашему прежнему рассмотрению отношений периметра и площади. Эта мера часто используется совместно с другими функциями, которые позволяют отделять каждый непрерывный полигон от полигонов с теми же самыми значениями атрибута. Другими словами, мы можем измерять конфигурацию границы каждого полигона отдельно от остальной части возможно фрагментированного региона, а не просто отмечать размер всего региона, составленного из нескольких отдельных полигонов.
Наиболее распространенной мерой пространственной целостности является функция Эйлера [Berry, 1993]. Одни виды, например, птицы, предпочитают большие непрерывные области определенного типа ландшафта, в то время как другие, такие как олени, ищут большие участки леса, перемежающиеся с меньшими участками лугов или других типов ландшафта. Участок леса, который не имеет разрывов, называется непрерывным; если он полностью окружает меньшие полигоны, то называется перфорированным; если он полностью отделен от аналогичных участков участками другого типа, тогда мы называем его фрагментированным. Функция Эйлера представляет численное выражение степени фрагментированности и перфорированности. Рассмотрим ее идею.
На рисунке 8.2 изображены три возможные конфигурации полигонов. Функция Эйлера сопоставляет с каждой из них одно число, называемое числом Эйлера (Euler number), которое определяется так:
E=H-(F-1), где Е - число Эйлера, Н - суммарное количество отверстий во всех полигонах региона, F - количество полигонов во фрагментированном регионе.
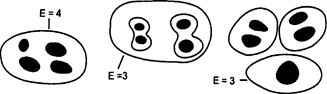
Рисунок 8.2. Примеры чисел Эйлера. Три различные конфигурации и связанные с ними числа Эйлера: а) четыре отверстия в одном сплошном регионе: 4+(1-1)=4;
b) два фрагмента, по два отверстия в каждом: 4-(2-1)=3; с) три фрагмента, два с двумя отверстиями каждый и третий - с одним: 5-(3-1)=3. Заметьте, что во втором и третьем случаях число Эйлера одно и то же, несмотря на то, что конфигурации различны.
Как следует из совпадения значений числа Эйлера для разных конфигураций, приведенных на Рисунках 8.2а и 8.2Ь, нужно осмотрительно подходить к объяснению результатов. Вы можете рассмотреть и другие конфигурации, в том числе дающие отрицательные значения числа Эйлера (например, область из трех фрагментов без отверстий: Е = 0 - (3 -1) = - 2). В Таблице 8.1 приведены некоторые конфигурации с соответствующими значениями числа Эйлера, из которой вы можете увидеть соотношения параметров, дающие одинаковые значения числа Эйлера.
Таблица 8.1. Числа Эйлера для различных комбинаций количеств отверстий (Н) и фрагментов (F).*
| F | |||||||||
| н | |||||||||
| -1 | -2 | -3 | -4 | -5 | -6 | -7 | |||
| -1 | -2 | -3 | -4 | -5 | -6 | ||||
| -1 | -2 | -3 | -4 | -5 | |||||
| -1 | -2 | -3 | -4 | ||||||
| -1 | -2 | -3 | |||||||
| -1 | -2 | ||||||||
| -1 | |||||||||
Вторая группа мер полигонов, относящихся к их границам, довольно многочисленна. Встречаются меры на основе отношения осей, на основе только периметра, на основе только площадей, на основе соотношений периметра и площади, площади и длин осей, а также другие, измеряющие, например, округлость сторон. Формулы для них вы можете найти в пятой главе одной хорошей книги по использованию математических методов в геологии [Davis, 1986], когда достаточно разовьется ваш интерес к анализу форм, и вы будете иметь достаточный опыт в геоинформатике для их использования. Одни специальные меры имеются в коммерческих ГИС, другие - в геостатистических программах или в составе дополнительных модулей коммерческих ГИС [Baker and Cai, 1992; McGarigal and Marks, 1994].
Большинство этих мер связано с отношением периметра к площади. На самом деле, само это отношение может рассматриваться как мера полигональной формы. Однако, оно не описывает реальную геометрическую форму объекта. Вместо простого отношения было бы неплохо иметь некоторую более "формообразную" меру. Для этого мы чаще всего сравниваем имеющиеся полигональные фигуры с более знакомыми фигурами, которые можем легко описать [Muehrcke and Muehrcke, 1992]. Например, мы могли бы сравнивать их с параллелограммами, трапециями и треугольниками. Но даже эти фигуры очень разнообразны, в то время как круг является наиболее простой, компактной и легко определимой фигурой. По этой причине основным методом измерения формы является сравнение ее с кругом.
* Отметьте количество конфигураций с одним числом Эйлера. Обратите также внимание на отражение с противоположным знаком чисел таблицы относительно главной диагонали.
В связи с использованием круга как сравнительной фигуры, мы можем говорить, что эта мера является также и меройвыпуклости или вогнутости (convexity or concavity) полигона. Круг является наиболее выпуклой фигурой, вот почему мы используем его для измерения формы других объектов. Как известно, все другие геометрические фигуры имеют большую длину периметра при том же значении площади. Сравнение имеющегося многоугольника с кругом, по сути, - то же, что рассмотрение величины выпуклости этого полигона по сравнению с выпуклостью круга. Общая формула выпуклости в векторных ГИС такова:
CI = k P/A,
где: CI - индекс выпуклости, k - некоторая константа, Р - периметр, А -площадь.
Здесь мы имеем отношение периметра к площади, умноженное на некоторую константу Эта константа определяется размером круга, описанного вокруг многоугольника, так что индекс принимает значения в диапазоне 1...99, причем большее значение соответствуют большему сходству с кругом, а 100 получается, если мы возьмем идеальный круг.
В растре формула основана на той же идее, но здесь площадь определяется как количество клеток, а квадратный корень из нее используется для получения того же диапазона 1...99 значений сходства. При этом надо помнить, что в растре мы физически не можем иметь идеальный круг. Формула определения выпуклости в растре такова:
CI=P/√N
где: CI - индекс выпуклости, Р - периметр, N - площадь в растровом формате.
Вернемся к вопросу о том, для чего же нужна мера выпуклости. Задайте себе такой вопрос: почему американские колонисты, атакуемые индейцами, выстраивали повозки в круг? Почему не в квадрат, треугольник или как-нибудь еще? Ответ состоит в том, что при заданной площади круг имеет наименьший периметр из всех фигур. Многие существа, в том числе и человек, ценят защитный характер круга, с его более легко обороняемым периметром. Хотя есть и такие, как, например, некоторые мелкие грызуны, которые любят края. Они используют эти края для вылазок на открытые Пространства полей, оставаясь при этом вблизи леса для бегства и укрытия.
Имеется еще одна мера конфигурации границ, называемаяразвитостью границы (edginess) [Berry, 1993], которая использует краевой фильтр.Фильтры(см. Главу 9), используемые для оценки или изменения растровых изображений, являются матрицами коэффициентов, которые применяются к ячейкам растра, находящимся в "окне" под матрицей. После выполнения операции с одной группой ячеек, матрица смещается на одну ячейку в сторону и операция повторяется, что дало названиескользящее окно (roving window). В дистанционном зондировании фильтры используются для двух основных задач - подчеркивания деталей (sharpening) и сглаживания (smoothing). Фильтры первого типа подчеркивают линии и края областей, второго - наоборот, ослабляют резкие переходы между значениями соседних ячеек растра. Хотя эти приложения фильтров больше ассоциируются с классификацией, мы рассматриваем их здесь как средства оценки конфигурации границ.
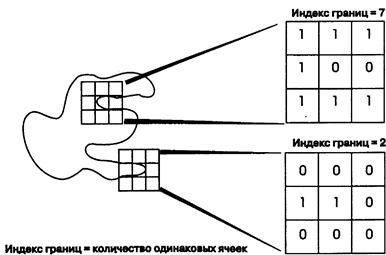
Рисунок 8.3. Развитость границ в растре. Использование скользящего окна для определения индекса границ.
Возьмем окно размером 3х3 ячейки, наложенное в двух местах границы области (Рисунок 8.3). Каждой ячейке матрицы мы присваиваем единицу, если она имеет тот же атрибут, что и край, который нас интересует, и ноль, если она имеет атрибуты любого другого объекта покрытия. Индекс границ получается простым подсчетом числа ячеек с единицами, т.е. таких, которые имеют то же значение атрибута, что и наш полигон. Чем больше единиц, тем меньше границ и тем больше внутренней области мы имеем. Поэтому, значение 7 на Рисунке 8.3 указывает на малую развитость границы. Значение
9 соответствует внутренней области полигона, где все ячейки растра соединены и вообще нет границ. И наоборот, значение 2 на Рисунке 8.3 показывает, что только небольшое число нужных ячеек растра имеется в окне, а остальные относятся к фону Оно указывает на небольшой узкий выступ в окружение. Иначе говоря, во втором случае окно покрывает большое количество краев.
Дата добавления: 2016-02-24; просмотров: 1654;
