Влияние температуры на скорость химической реакции.
Опыт показывает, что с повышением температуры скорость химической реакции возрастает. В уравнении химической кинетики v = kCACBвлияние температуры практически сказывается на изменении константы скорости реакции k. С возрастанием температуры растет величина константы k, следовательно, увеличивается сама скорость реакции.
Если через kTобозначить константу скорости данной реакции при температуре Т, а через kт+10К— константу скорости той же реакции при температуре (Т+ 10К), отношение второй величины к первой даст так называемый температурный коэффициент скорости реакции (у):
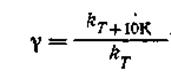
| 2.24 |
 Согласно приближенному (эмпирическому) правилу Вант-Гоффа величина температурного коэффициента у колеблется в пределах 2—4, т. е. при повышении температуры на 10 К скорость химической реакции возрастает в два— четыре раза. Например, если принять температурный коэффициент равным 2, легко можно подсчитать, что при повышении температуры на 100 К скорость реакции увеличится в 1024 раза.
Согласно приближенному (эмпирическому) правилу Вант-Гоффа величина температурного коэффициента у колеблется в пределах 2—4, т. е. при повышении температуры на 10 К скорость химической реакции возрастает в два— четыре раза. Например, если принять температурный коэффициент равным 2, легко можно подсчитать, что при повышении температуры на 100 К скорость реакции увеличится в 1024 раза.
Согласно правилу Вант-Гоффа температурный коэффициент скорости γ для каждой химической реакции должен являться величиной постоянной. Однако в действительности он сильно уменьшается при повышении температуры, поэтому правило Вант-Гоффа справедливо лишь в сравнительно узком интервале температур.
Более точная зависимость константы скорости химической реакции от температуры была найдена Аррениусом (1889). Уравнение Аррениуса имеет вид
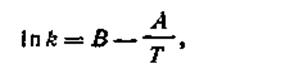
| 2.25 |
где k — константа скорости реакции; А и В — постоянные, характерные для данной реакции; Т — термодинамическая температура.
Из уравнения (2.25) видно, что логарифм константы скорости находится в линейной зависимости от обратной температуры, т. е.
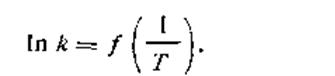
| 2.26 |
Коэффициенты А и В вуравнении Аррениуса могут быть определены путем решения системы из двух уравнений для двух температур или определены графическим способом. Так, если по экспериментальным данным построить график зависимости ln k—1/T, то угловой коэффициент прямой определяет величину A = tg a, а постоянная В определяется отрезком, отсекаемым прямой на оси ординат (рис. 2.2). Определив таким путем численные значения постоянных А и В для данной реакции, можно вычислить константу скорости, а следовательно, и скорость этой реакции при любой температуре.
 Величина А в уравнении (2.26) характеризует так называемую энергию активации Е химического процесса. Поясним смысл энергии активации несколько более подробно.
Величина А в уравнении (2.26) характеризует так называемую энергию активации Е химического процесса. Поясним смысл энергии активации несколько более подробно.
Известно, что реакционноспособны только те молекулы, которые обладают запасом энергии, необходимым для осуществления той или иной реакции, т. е. избыточной энергией по сравнению со средней величиной энергии молекулы. Такие молекулы получили название активных молекул. Эта избыточная энергия активной молекулы, благодаря которой становится возможной химическая реакция, носит название энергии активации. Эту энергию обычно выражают в кДж/кмоль. Энергия активации бывает меньше энергии разрыва связей в молекуле, так как для того чтобы молекула прореагировала, вовсе не требуется полного разрыва связей, их достаточно лишь ослабить.
Величина энергии активации зависит от строения молекулы и от того, в какую реакцию эта молекула вступает. Иными словами, каждая химическая реакция характеризуется свойственной ей величиной энергии активации. Ниже приведены значения Е (кДж/кмоль) для некоторых реакций:
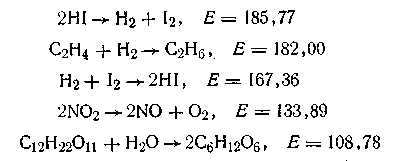
Энергия активации молекул может быть снижена под воздействием внешних факторов: повышение температуры, лучистой энергии, катализаторов и др. Энергия активации проявляется в активных молекулах по-разному: активные молекулы могут обладать большей скоростью движения, повышенной энергией колебания атомов в молекуле и др.
На рис. 2.3 показано, что скорость реакции пропорциональна числу активных молекул и зависит от величины энергии активации. На этом рисунке по оси ординат отложена энергия рассматриваемой системы молекул, а по оси абсцисс — ход реакции. Если реакция перехода из состояния I в состояние II идет с выделением тепла, т. е. является экзотермической, то общий запас энергии продуктов реакции меньше, чем исходных веществ. При этом разность энергетических уровней I и II равна тепловому эффекту реакции Q. Энергетический уровень К характеризует то наименьшее количество энергии, которым должны обладать молекулы, чтобы при столкновении друг с другом они прореагировали. Разность между уровнем К и уровнем I характеризует энергию активации Е1 прямой реакции, а разность между уровнями К и II — энергию активации обратной реакции Е2. Таким образом, при переходе из состояния I в состояние II система должна преодолеть энергетический барьер, т. е. должна обладать определенным избытком энергии, чтобы вступить в химическое взаимодействие.
Следовательно, скорость химической реакции зависит от величины энергии активации: чем она больше, тем медленнее будет протекать данная реакция. С другой стороны, чем меньше энергетический барьер реакции, тем большее число молекул будет обладать необходимой избыточной энергией и тем быстрее будет протекать эта реакция. Итак, скорость химической реакции в конечном итоге зависит от соотношения между числом активных и неактивных молекул.
В теории активных соударений Аррениус показал, что количество активных молекул может быть вычислено по закону Максвелла — Больцмана:
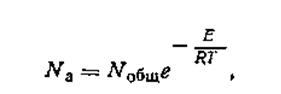
| 2.27 |
где Nа—число активных молекул; Nобщ — общее число молекул; e — основание натуральных логарифмов; Е — энергия активации; Т — термодинамическая температура; R — универсальная газовая постоянная. Уравнению (2. 28) можно придать вид
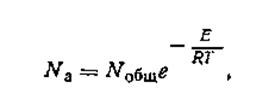
| 2.28 |
или после логарифмирования
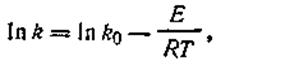
| 2.29 |
где k —константа скорости реакции при обычных условиях; k0 — константа скорости при условии, что все столкновения приводят к реакции.
Сравнение уравнений (2.25) и (2.29) позволяет выяснить физический смысл констант в уравнении Аррениуса. A = E/R характеризует энергию активации процессов (Е), a B =ln k0, т. е. равно логарифму числа столкновений за 1 с в единице объема.
Если известны константы скорости k1и k2при двух температурах T1 и T2, можно найти значение Е из уравнения (2.30):
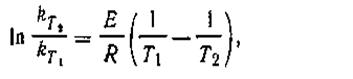
| 2.30 |
или, заменяя натуральные логарифмы десятичными и вводя вместо R его численное значение 8,315 Дж/(моль·К), можно записать:
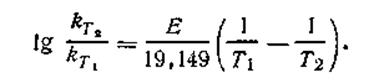
| 2.31 |
Таким образом, рост скорости реакции с повышением температуры объясняется тем, что с увеличением температуры увеличивается не только средняя кинетическая энергия молекул, но и одновременно, как следует из уравнения (2.28), резко возрастает доля молекул, обладающих энергией выше определенного уровня, т. е. доля активных молекул, способных к реакции.
Дата добавления: 2016-02-20; просмотров: 2023;
