Основные положения и понятия в технологии машиностроения
В природе существует ничтожно малое количество предметов, которые может использовать человек непосредственно без преобразования. Поэтому человеку приходиться приспосабливать предметы природы для удовлетворения своих потребностей.
Современный человек стремиться преобразования предметов природы выполнять с помощью машин.
Человеческое общество постоянно испытывает потребности в новых видах продукции, либо в сокращении затрат труда при изготовлении освоенной продукции. Эти потребности могут быть удовлетворены с помощью новых технологических процессов и новых машин. Таким образом, стимулом к созданию новой машины всегда является новый технологический процесс.
Машина полезна лишь, если она обладает требуемым качеством и, т.о., способна удовлетворять потребность людей.
Ресурсы труда в жизни человеческого общества представляют собой наивысшую ценность.
Создавая машину, человек ставит перед собой две задачи:
1. создать машину качественной
2. затратить меньшее количество труда при создании машины
Замысел новой машины возникает при разработке технологического процесса изготовления продукции, в производстве которой возникла потребность. Этот замысел выражается в формулировке служебного назначения, которая является исходным документом для проектируемой машины.
Процесс создания машины состоит из двух этапов:
1. проектирование
2. изготовление
В результате проектирования появляются чертежи машины. В результате изготовления с помощью производственного процесса появляется машина.
Второй этап и составляет основную задачу технологии машиностроения. Создание машины можно представить в виде схемы (рис.1.1). Изготовление машины связано с использованием различных способов обработки металлов.
История возникновения металлообработки в России мало исследована, однако известно, что:
· в X в. Русские ремесленники обладали высокой техникой изготовления оружия, предметов обихода и т.п.;
· в XII в. Русские оружейники применяли сверлильные и токарные устройства с ручным приводом и вращательным движением инструмента или заготовки;
· в XIV – XVI в.в. использовались токарные и сверлильные устройства с приводом от ветряной мельницы;
· в XVI в. в селе Павлове на Оке и в окрестностях г. Тулы существовала металлообрабатывающая промышленность;
· А.И.Нартов (1718—1725) создал механический суппорт для токарного станка;
· М.В. Сидоров (1714) на тульском оружейном заводе создал «вододействующие» машины для сверления оружейных стволов;
· Яков Батищев построил станок для одновременного сверления 24 ружейных стволов;
· М.В.Ломоносов (1711-1765) построил лоботокарные, сферотокарные и шлифовальные станки;
· И.И.Ползунов (1728-1764) построил цилиндрорасточные и др. станки для обработки деталей паровых котлов;
· И.П.Кулибин (1735-1818) построил станки для изготовления зубчатых колес часовых механизмов;
· в конце XIX и начале XX в.в. на некоторых предприятиях начали указывать на рабочих чертежах допуски на изготовление деталей.
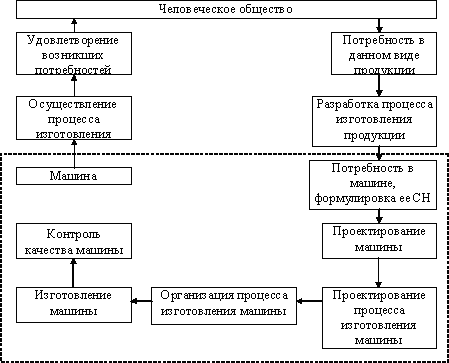
Рис. 1.1. Создание машины
Зарождение технологии машиностроения, как отрасли науки связывают появлением трудов, содержащих описание опыта производство процесса.
Впервые сформулировал положение о технологии и определил, что «технология – наука о ремеслах и заводах» в 1804 г. Академик В.М.Севергин. А в 1817 г. Впервые был изложен опыт производства профессором Московского университета И.А. Двигубским в книге «Начальные основания технологии или краткое описание работ, на заводах и фабриках производимых».
Дальнейшее описание выполнено Тиме И.А. (1838-1920 г.г.) в первом капитальном труде «Основы машиностроения. Организация машиностроительных фабрик в техническом и экономическом отношении и производство в них работ», вышедшим в 1885 г. Позже Гавриленко А.П. (1861-1914г.г.) создал курс «Технология металлов».
Затем появились работы не просто обобщающие опыт, но и выявляющие общие зависимости и закономерности. Соколовский А.П. в 1930-1932 г.г. издал первый труд по технологии машиностроения. В 1933 г. Появился труд Каширина А.И. «Основы проектирования технологических процессов» и «Теория размерных цепей», разработанная Балакшиным Б.С., а в 1935г. – «Технология автотракторостроения», в котором Кован В.М. и Бородачев Н.А. занимались анализом качества и точности производства. Исследованием жесткости, применительно к станкам, в 1936 г. занимался Вотинов К.В. Работы ЗыковаА.А. и Яхина А.Б. положили начало анализу причин возникновения погрешностей при обработке. В 1959 г. Кован В.М. разработал методику расчета припусков. Исследования в области технологии машиностроения продолжили Глейзер Л.А., Корсаков В.С., Колесов И.М., Чарнко Д.В. и др.,
Технология машиностроения как наука (в современном понимании) прошла в своем развитии несколько этапов. Маталин А.А., автор одного из учебников по технологии машиностроения, выделяет четыре этапа.
Первый этап (до1929-1930 г.г.) характеризуется накоплением отечественного и зарубежного производственного опыта изготовления машин. Публикуются описания процессов обработки различных деталей, применяемого оборудования и инструментов. Издаются руководящие и нормативные материалы ведомственных проектных организаций страны.
Второй этап (1930-1941 г.г.) характеризуется обобщением и систематизацией накопленного производственного опыта и началом разработки общих научных принципов построения технологических процессов.
Третий этап (1941-1970 г.г.) отличается интенсивным развитием технологии машиностроения, разработкой новых технологических идей и формированием научных основ технологической науки.
Четвертый этап – с 1970 г. По настоящее время отличается широким использованием достижений фундаментальных и общеинженерных наук для решения теоретических проблем и практических задач технологии машиностроения.
Современное представление технологии машиностроения – это отрасль технической науки, которая изучает связи и закономерности в производственных процессах изготовления машин.
Конструкция любой машины – сложная система двух видов сопряженных множеств связей:
1. свойств материалов;
2. размерных.
Для реализации такой системы связей должен быть создан и осуществлен производственный процесс, который представляет собой другую систему сопряженных множеств связей:
1. свойств материалов (нужны для создания аналогичных связей в машине во время производственного процесса);
2. размерных;
3. информационных (для управления производственным процессом);
4. временных и экономических (производственный процесс не может осуществляться вне времени и без затрат живого и овеществленного труда).
Таким образом, создание машины сведены к построению двух систем связей (рис.1.2):
1. конструкции машины;
2. производственного процесса изготовления.
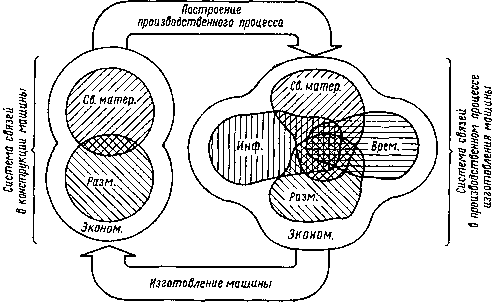
Рис.1.2. Системы связей в машине
1.1. Понятие о машине и ее служебное назначении
Машина- устройство, предназначенное для действия в нем сил природы сообразно потребностям человека.
В настоящее время понятие «машина» имеет ряд смыслов:
· машина — механизм или сочетание механизмов, выполняющих движение для преобразования энергии, материалов или производства – с точки зрения механики;
· машина – доменная печь (Менделеев Д.И.);
· машина (с появлением ЭВМ) – механизм или сочетание механизмов, осуществляющих определенные целесообразные движения для преобразования энергии, выполнения работы или же для сбора, передачи, хранения, обработки и использования информации.
И, наконец, с точки зрения технологии машиностроения: машина является либо объектом, либо средством производства.
Поэтому машина – система, созданная трудом человека, для качественного преобразования исходного продукта в полезную для человека продукцию (рис.1.3).
Исходный продукт процесса – предметы природы, сырье или полуфабрикат.
Сырье– предмет труда, на добычу или производство которого, был затрачен труд.
Полуфабрикат– сырье, которое подвергалось обработке, но не может быть потреблено как готовый продукт.
Продукция– это результат производства в виде сырья, полуфабриката, созданных материальных и культурных благ или выполненных работ производственного характера (табл. 1.1).
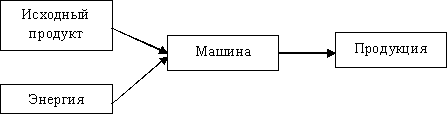
Рис. 1.3. Машина – средство производства
Таблица 1.1. Преобразования машинами исходного продукта в продукцию
| Исходный продукт | Энергия | Машина | Продукция |
| Заготовка | Электроэнергия | Станок | Деталь |
| Груз | Механическая | Автомобиль | Перевезенный груз |
| Ткань, нить | Механическая | Швейная машина | Шов |
| Эл. магнитные волны | Электрическая | Телевизор | Изображение и звук |
| Задача | Электрическая | ЭВМ | Решенная задача |
| Энергия сгораемого топлива | Расширения газов | Двигатель внутреннего сгорания | Механическая энергия |
Каждая машина создается для выполнения определенного процесса, т.е. имеет свое, строго определенное предназначение, иными словами — свое служебное назначение.
Под служебным назначениеммашины понимают четко сформулированную задачу, для решения которой предназначена машина.
Формулировка служебного назначения машины должна содержать подробные сведения, конкретизирующие общую задачу и уточняющие условия, при которых эта задача может быть решена. Например, автомобиль или обувь:
| Автомобиль | Обувь |
| Сведений только о перевозке грузов недостаточно, чтобы представить нужный автомобиль. Необходимо знать: характер грузов, их массу и объем, условия, расстояние и скорость перевозки, состояние дорог, климат, внешний вид и т.д. | Сведения о защите ног недостаточно, чтобы удовлетворить потребность в обуви. Необходимо знать: размер, климат, время года, состояние дорог, внешний вид и т.д. |
Служебное назначение машины описывают не только словесно, но и системой количественных показателей, определяющих ее конкретные функции, условия работы и т.д. Формулировка служебного назначения машины является важнейшим документом в задании на ее проектирование.
1.2. Качество и экономичность машины
Машина (как рассматривали выше) либо средство производства, либо объект производства – продукция. Поэтому машина, являясь одной из разновидностей продукции, обладает качеством и экономичностью.
Под качеством машины понимают совокупность ее свойств, обуславливающих способность выполнять свое служебное назначение. К показателям качества машины относят те, которые характеризуют меру полезности машины, т.е. ее способность удовлетворять потребности людей в соответствии со своим назначением. К ним относятся:
· качество продукции производимой машиной;
· производительность;
· надежность;
· долговечность (физическая и моральная);
· безопасность работы;
· удобство управления;
· уровень шума;
· КПД;
· степень механизации и автоматизации;
· техническая эстетичность и т.п.
Проектирование машины, ее изготовление, эксплуатация, техническое обслуживание и ремонт связано с конкретными затратами труда и материалов, энергии, технических средств. Все затраты образуют стоимостное свойство машины – ее экономичность.

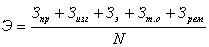 ,
,
где: 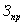 — затраты на проектирование;
— затраты на проектирование;
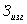 — затраты на изготовление
— затраты на изготовление
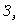 — затраты на эксплуатацию;
— затраты на эксплуатацию;
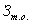 — затраты на техническое обслуживание;
— затраты на техническое обслуживание;
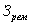 - затраты на ремонт;
- затраты на ремонт;
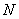 — количество продукции, произведенной машиной за ее срок службы.
— количество продукции, произведенной машиной за ее срок службы.
Между качеством и экономичностью машины существуют связи, приводящие к влиянию одних на другие. Например:
· повышение качества по любому показателю связано с увеличением ее стоимости;
· в то же время повышение уровня надежности машины, сокращает затраты на устранение отказов, технического обслуживания и ремонт.
Потребление машиной энергии, топлива, материалов при эксплуатации, в известной мере, характеризующее экономичность машины, во многом зависит от качества ее изготовления и т.п.
Показатели качества отражают степень пригодности, полезности, те блага, которые извлекает человек, используя свою машину.
Экономичность – цена этих благ, их стоимость.
Качество машин обеспечивается уровнем проектных решений, от которого зависит техническое совершенство конструкции машины и технологией, определяющей качество сборки и отделки машины.
Экономичность машины зависит от технического совершенства конструкции машины и технологии ее изготовления. Стоимость машины зависит от качества, количества и стоимости материалов, выбранных конструктором в процессе проектирования. Конечные затраты на материалы, входящие в себестоимость, можно определить лишь уровень после осуществления технического процесса ее изготовления.
Уровень унификации и технологичности машины определяет конструктор. Влияние этих факторов на себестоимость машины проявляется не прямым путем, а через технологию ее изготовления. Эти же факторы оказывают влияние на затраты по технологическому обслуживанию и ремонту.
Экономическими показателями являются потребление машиной энергии, потребление машиной топлива, потребление машиной материалов в процессе эксплуатации.
Но вместе с тем, на значение этих показателей влияет качество реализации технологического процесса и т.д. Таким образом, обеспечение качества и экономичность машины в процессе ее создания является общей задачей конструктора и технолога.
Проблема создания качественных и экономичных машин является важнейшей и наиболее сложной. Сложно не только создание конструкции машины, но и обеспечение ее качества и экономичности при конструировании и изготовлении, так как любая машина создается для выполнения процесса, наделенного вероятностными свойствами, а изготовление сопровождается явлениями случайного характера.
ЛЕКЦИЯ 2
2.Положение теории вероятности и математической статистики, используемые в технологии машиностроения
2.1.Основные положения
Случайная величина, которая в зависимости от случая принимает те или иные значения с определенной вероятностью. Случайные величины могут иметь различный характер. Случайная величина может быть, например:
· скалярной величиной;
· вектором;
· функцией;
· и др.
С каждой случайной величиной можно связать определенное событие.
Событие, которое может произойти или не произойти в результате данного опыта, называется случайным. Количественной оценкой возможности появления случайного события 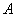 служит вероятность
служит вероятность 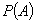 .
.
Вероятностью события 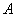 называют отношение числа случаев
называют отношение числа случаев 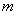 , благоприятствующих этому событию, к числу n всех возможных случаев в данном опыте:
, благоприятствующих этому событию, к числу n всех возможных случаев в данном опыте:
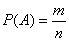 .
.
При этом все случаи должны быть равно возможны, несовместимы и независимы.
Вероятность события является объективной мерой его возможности и определяется в предположении проведения очень большого числа опытов, в результате которых появляется данное событие, поэтому эта величина имеет теоретический характер.
Практической характеристикой возможности случайного события 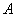 служит частость события
служит частость события 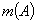 , представляющая собой отношение частоты
, представляющая собой отношение частоты 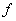 появления события
появления события 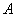 к общему числу
к общему числу 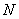 проведенных опытов:
проведенных опытов:
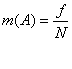 .
.
Между вероятностью и частотой какого-либо события существует приближенное равенство:
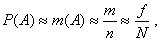
которое будет тем точнее, чем больше число опытов.
Характеристикой случайной величины служит закон ее распределения.
Под распределением случайной величины понимают совокупность ее значений, расположенных в возрастающем порядке, с указанием либо их вероятностей в теоретическом, либо частостей в практическом распределении.
Практическое распределение случайных величин дискретного характера можно представить в виде таблицы (табл.2.1) или графика 2.1, составленного на основании таблицы 2.1.
Таблица 2.1. Практическое распределение дискретной случайной величины
| X | ||||||
| m(xi) | 1/20 | 3/20 | 8/20 | 5/20 | 3/20 | 
|
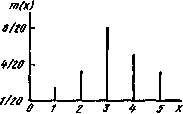
Рис.2.1. Распределение случайной дискретной величины
Распределение случайной величины непрерывного типа может быть также представлено в виде таблицы или графика. Для составления таблицы практического распределения непрерывной случайной величины в совокупности ее значений находят max и min и определяют разность между ними. Разность эта называется полем рассеивания 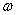 случайной величины:
случайной величины:
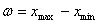 .
.
Значения случайной величины, составляющие совокупность, делят на равные интервалы. Их число « 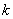 » определяют из отношения значения
» определяют из отношения значения 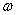 к избранному значению «
к избранному значению « 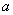 » интервала:
» интервала:
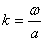 .
.
Относя каждое значение случайной величины к тому или иному интервалу, подсчитывают частоты ее значений в границах интервалов и определяют частости значений 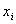 . Например. Пусть в партии валов из 100 штук диаметр одной из шеек
. Например. Пусть в партии валов из 100 штук диаметр одной из шеек 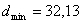 мм, а другой
мм, а другой 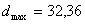 мм. Тогда
мм. Тогда 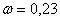 мм.
мм.
При избранном значении интервала 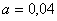 мм число
мм число 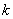 будет равно:
будет равно:
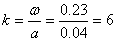 .
.
Установив границы и подсчитав частости, получают таблицу распределения значений 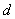 вала:
вала:
| 1) | 32,13 – 32,16 | 0,03 | |
| 2) | 32,17 – 32,20 | 0,11 | |
| 3) | 32,21 – 32,24 | 0,36 | |
| 4) | 32,25 – 32,28 | 0,40 | |
| 5) | 32,29 – 32,32 | 0,6 | |
| 6) | 32,33 – 32,36 | 0,04 |
Графически практическое распределение непрерывной случайной величины может быть представлено либо гистограммой, либо практической кривой (полигоном) распределения (рис.2.2.).
Общей формой закона распределения случайной величины является ее функция распределения. Функцией распределения или интегральным законом распределения скалярной случайной величины 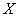 называют вероятность выполнения неравенства
называют вероятность выполнения неравенства 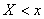 :
:
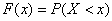 ,
,
где 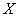 – случайная величина,
– случайная величина,
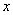 – возможные значения случайной величины.
– возможные значения случайной величины.
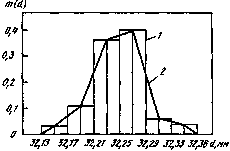
Рис.2.2. Гистограмма и практическая кривая распределения непрерывной случайной величины
Для дискретной случайной величины 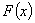 может быть найдено по таблице или графику распределения для любого значения
может быть найдено по таблице или графику распределения для любого значения 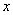 , как сумма вероятностей тех значений
, как сумма вероятностей тех значений 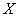 , которые лежат влево от точки с координатой
, которые лежат влево от точки с координатой 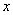 . В рассмотренном выше примере распределения случайной величины для
. В рассмотренном выше примере распределения случайной величины для 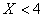 .
.
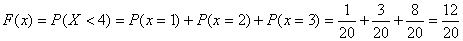 .
.
Интегральный закон распределения можно представить в виде графика 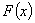 . Для дискретной случайной величины график будет иметь вид ступенчатой кривой.
. Для дискретной случайной величины график будет иметь вид ступенчатой кривой.
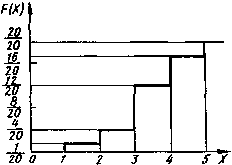
Рис.2.3. Интегральный закон распределения дискретной случайной величины
Имея функцию распределения дискретной случайной величины можно вычислить вероятность ее нахождения в границах от 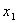 до
до 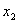 :
:
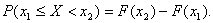
Для непрерывной случайной величины график функции распределения будет иметь вид монотонно возрастающей кривой, а сама функция будет дифференцируемой.
Производную 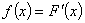 функции распределения
функции распределения 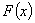 непрерывной случайной величины
непрерывной случайной величины 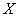 называют плотностью вероятности или дифференциальным законом распределения этой случайной величины.
называют плотностью вероятности или дифференциальным законом распределения этой случайной величины.
Графически этот закон распределения может быть представлен кривой линией, построенной в координатах x, 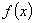 (рис.2.4).
(рис.2.4).
Зная плотность вероятности, можно определить вероятность того, что значение случайной величины 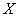 окажется в интервале от
окажется в интервале от 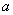 до
до 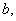 .
.
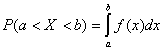 .
.
В данном случае вероятность равна площади участка с основанием « 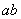 », ограниченного сверху кривой плотности вероятности. При
», ограниченного сверху кривой плотности вероятности. При 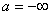 и
и 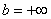 :
:
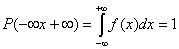 .
.
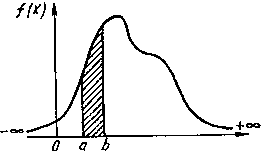
Рис.2.4. Дифференциальный закон распределения непрерывной случайной величины
Дифференциальный закон или плотность вероятности дает полную картину распределения случайной величины. Однако такая полная характеристика не всегда необходима. В ряде теоретических и практических задач бывает достаточным знание отдельных числовых характеристик:
· определяющих положение центра группирования случайной величины 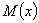 ;
;
· ее рассеяние около этого центра.
Для характеристики положения центра группирования используют математическое ожидание и среднее арифметическое значение случайной величины:
а) для дискретной случайной величины:
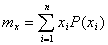 ,
,
где 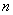 – число возможных значений случайной величины
– число возможных значений случайной величины 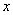 ;
;
б) для непрерывной случайной величины:
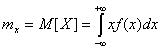 ,
,
где 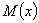 – характеристика теоретического распределения случайной величины.
– характеристика теоретического распределения случайной величины.
На практике положение центра группирования 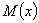 характеризует среднее арифметическое значение случайной величины:
характеризует среднее арифметическое значение случайной величины:

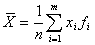 ,
,
где 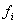 – частота отдельных значений
– частота отдельных значений 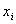 ,
,
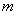 – число отдельных значений
– число отдельных значений 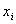 ,
,
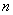 – общее отдельных значений
– общее отдельных значений 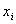 .
.
Характеристикой рассеяния значений случайной величины около центра группирования 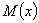 является дисперсия. Однако чаще используют не саму дисперсию, а положительный квадратный корень из нее, называемый средним квадратичным отклонением:
является дисперсия. Однако чаще используют не саму дисперсию, а положительный квадратный корень из нее, называемый средним квадратичным отклонением:
а) дисперсия и среднее квадратичное отклонение дискретной случайной величины
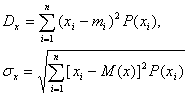 ;
;
б) дисперсия и среднее квадратичное отклонение непрерывной случайной величины
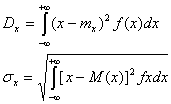 .
.
Для практических распределений среднее квадратическое отклонение определяется по формуле:
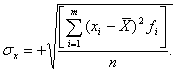
Размерность  x совпадает с размерностью самой случайной величины.
x совпадает с размерностью самой случайной величины.
Таким образом, чтобы охарактеризовать распределение случайной величины надо иметь как минимум две числовые характеристики:
1. 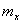 или
или 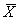 – определяют положение центра группирования;
– определяют положение центра группирования;
2. 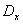 или
или 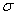 x – разброс значений случайной величины около центра группирования.
x – разброс значений случайной величины около центра группирования.
Комплектом характеристик распределения следует считать также:
· поле рассеяния случайной величины:
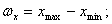
· — координату середины поля рассеяния:
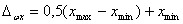 .
.
В симметричных распределениях центр группирования 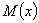 оказывается совмещенным с
оказывается совмещенным с 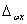 .
.
2.2. Законы распределения
Распределение случайных величин в зависимости от условий могут подчиняться вполне определенным законам: Гаусса, равной вероятности, Симпсона. Наибольшее практическое значение в технологии машиностроения имеет дифференциальная функция закона нормального распределения (закон Гаусса), для которого плотность вероятности или дифференциальная функция распределения:
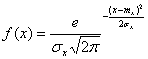 ,
,
где 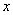 – переменная случайная величина;
– переменная случайная величина;
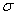 x – среднее квадратичное отклонение
x – среднее квадратичное отклонение 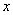 от
от 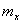 ;
;
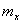 – математическое ожидание величины
– математическое ожидание величины 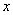 .
.
Дифференциальная функция закона нормального распределения графически изображается холмообразной кривой, симметричной относительно центра группирования, представленной величинами 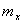 и
и 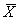 (рис.2.5). Координата центра группирования определяет положение кривой относительно начала отсчета, а параметр
(рис.2.5). Координата центра группирования определяет положение кривой относительно начала отсчета, а параметр 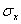 (среднее квадратичное отклонение) – ее форму и размах.
(среднее квадратичное отклонение) – ее форму и размах.
Функция или интегральный закон нормального распределения в общем виде можно записать:
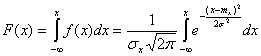 .
.
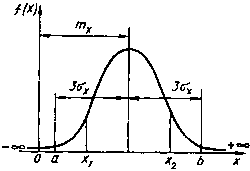
Рис.2.5. Дифференциальный закон нормального распределения случайной величины
Закон равной вероятности встречается, когда наряду со случайными факторами, вызывающими рассеяние, действует доминирующий систематический фактор непрерывно или равномерно изменяющий во времени положение центра группирования 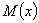 . Графически такое распределение случайной величины отображается прямоугольником (рис.2.6).
. Графически такое распределение случайной величины отображается прямоугольником (рис.2.6).
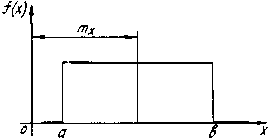
Рис.2.6. Распределение случайной величины по закону равной вероятности
Математическое ожидание, дисперсия и среднее квадратичное отклонение соответственно равны:

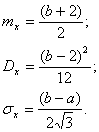
К распределению по закону Симпсона (закон треугольника) приводит сложение двух случайных величин, подчиненных закону равной вероятности при одинаковых параметрах рассеяния. Графически кривая рассеяния имеет вид равностороннего треугольника (рис.2.7).
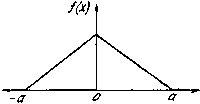
Рис.2.7. Распределение случайной величины по закону Симпсона
Математическое ожидание, дисперсия и среднее квадратичное отклонение соответственно равны:
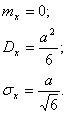
Если рассматривать распределение по законам Симпсона и равной вероятности как отклонение от закона нормального распределения, то можно отразить и количественную сторону этих отклонений с помощью коэффициента 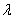 , который называется относительным средним квадратичным отклонением:
, который называется относительным средним квадратичным отклонением:
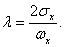
Значения коэффициента 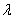 для рассмотренных законов распределения приведены в табл.2.3. На практике чаще пользуются значением коэффициента возведенного в квадрат.
для рассмотренных законов распределения приведены в табл.2.3. На практике чаще пользуются значением коэффициента возведенного в квадрат.
Таблица 2.3. Значения относительного среднего квадратичного отклонения
| Закон распределения | 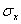
| 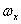
| 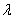
| 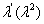
|
| Нормальный (Гаусса) | 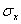
| 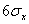
| 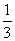
| 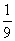
|
| Симпсона | 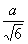
| 2a | 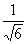
| 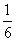
|
| Равной вероятности | 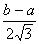
| b-a | 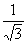
| 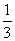
|
ЛЕКЦИЯ 3
3. Положение теории вероятности применительно к векторным случайным величинам
3.1. Векторные случайные величины.
При совместном рассмотрении двух случайных величин 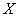 и
и 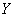 их можно трактовать как координаты случайной точки на плоскости или как составляющие случайного вектора
их можно трактовать как координаты случайной точки на плоскости или как составляющие случайного вектора 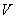 .
.
Функцией распределения двумерного случайного вектора с составляющими 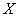 и
и 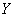 или совместной функцией распределения случайных величин
или совместной функцией распределения случайных величин 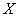 ,
, 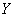 называют вероятность совместного выполнения неравенств
называют вероятность совместного выполнения неравенств 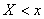 ,
, 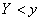 , рассматривая как функцию переменных
, рассматривая как функцию переменных 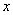 и
и 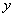 :
:

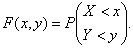
Функция распределения двумерного случайного вектора представляет собой вероятность попадания конца этого вектора в четверть плоскости, заштрихованную на рис.3.1.
Рис.3.1. Поверхность распределения двумерного случайного вектора
Вероятность попадания конца вектора в прямоугольник, ограниченный прямыми 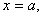
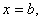
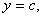
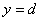 (рис.3.2):
(рис.3.2):
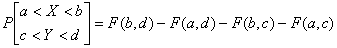
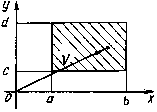
Рис.3.2. Распределение случайного вектора 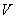 в прямоугольнике
в прямоугольнике 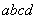
Плотность вероятности двумерного случайного вектора 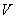 , составляющими которого являются случайные величины
, составляющими которого являются случайные величины 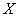 и
и 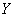 , или совместная плотность вероятности этих величин:
, или совместная плотность вероятности этих величин:
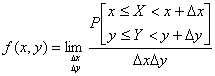 .
.
Вероятность попадания точки 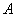 в произвольную область
в произвольную область 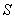 плоскости выражается интегралом от плотности вероятности, распространенным на эту область (рис.3.3):
плоскости выражается интегралом от плотности вероятности, распространенным на эту область (рис.3.3):
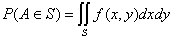 ,
,
где 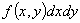 – вероятность попадания случайной точки
– вероятность попадания случайной точки 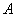 в элемент площади
в элемент площади 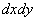 , расположенной в точке с координатами
, расположенной в точке с координатами 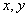 .
.
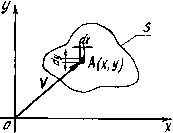
Рис.3.3. Распределение случайного вектора 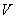 в области
в области 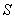
Математическим ожиданием случайного вектора 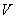 является вектор с составляющими, равным математическим ожиданиям величин
является вектор с составляющими, равным математическим ожиданиям величин 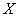 и
и 
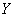 , и представляющий собой векторную сумму этих величин:
, и представляющий собой векторную сумму этих величин:
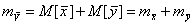 .
.
Геометрически математическое ожидание представляет собой радиус-вектор средней точки попадания конца вектора 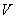 в область
в область 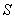 . Если случайные величины
. Если случайные величины 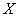 и
и 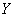 ,образующие вектор
,образующие вектор 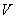 , не связаны, то теоретическими характеристиками рассеяния на плоскости являются дисперсии
, не связаны, то теоретическими характеристиками рассеяния на плоскости являются дисперсии 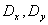 или средние квадратические отклонения
или средние квадратические отклонения 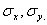
Если случайные величины 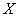 и
и 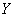 связаны, то в дополнение к дисперсии необходимо задавать вероятностную характеристику связи составляющих случайного вектора
связаны, то в дополнение к дисперсии необходимо задавать вероятностную характеристику связи составляющих случайного вектора 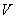 – корреляционный момент:
– корреляционный момент:
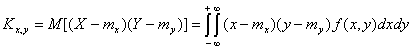 .
.
Таким образом, рассеяние возможных значений случайного вектора 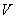 на плоскости характеризуется:
на плоскости характеризуется:
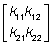
где
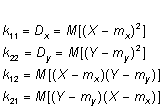 .
.
Причем 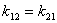 и при отсутствии связи между величинами
и при отсутствии связи между величинами 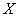 и
и 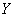 их значения равны нулю.
их значения равны нулю. 
Корреляционная матрица случайного вектора не изменится от прибавления к случайному вектору произвольного неслучайного вектора. Геометрически это свойство проявляется в том, что рассеяние случайного вектора на плоскости не зависит от выбора начала отсчета, что позволяет рассматривать рассеяние отклонений случайного вектора от его математического ожидания вместо рассеяния самого случайного вектора.
При распределении по нормальному закону, рассеяние на плоскости его отклонений от математического ожидания, ограничивается эллипсом, называемым эллипсом рассеяния. Центр эллипса находится в точке с координатами 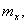
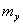 . Оси эллипса называются осями рассеяния, а характеристики рассеяния – главными дисперсиями
. Оси эллипса называются осями рассеяния, а характеристики рассеяния – главными дисперсиями 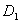 и
и 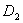
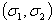 (рис.3.4).
(рис.3.4).
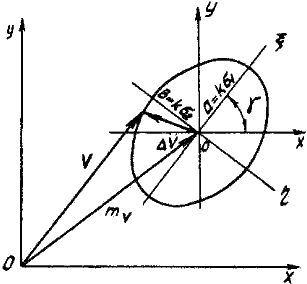
Рис.3.4. Эллипс рассеяния.
Эллипс рассеяния представляет собой геометрическое место точек равных плотностей вероятности. Полуоси эллипса пропорциональны главным средним квадратичным отклонениям:
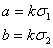 .
.
Большая ось эллипса рассеяния наклонена к оси 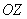 под углом
под углом 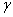 :
:
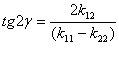 .
.
При 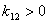 угол лежит в 1 и 3 четверти, а при
угол лежит в 1 и 3 четверти, а при 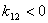 — во 2 и 4 четверти.
— во 2 и 4 четверти.
Значения дисперсий:
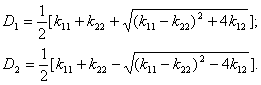
Вероятность попадания случайной точки, распределенной по нормальному закону, в область S, ограниченную эллипсом рассеяния:
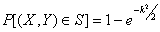 ,
,
где 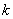 – размеры полуосей эллипса в средних квадратичных отклонениях. Если
– размеры полуосей эллипса в средних квадратичных отклонениях. Если 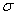 1=
1= 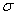 2=
2= 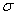 , то рассеяние по нормальному закону называется круговым.
, то рассеяние по нормальному закону называется круговым.
На практике возникает задача определения характеристик рассеяния случайного вектора на основании наблюдаемых значений случайного вектора в нескольких несвязанных опытах. Ограниченность числа опытов позволяет лишь предполагать приближение к теоретическим значениям характеристик, найденных по формулам:
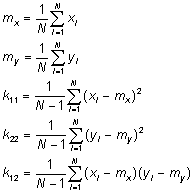
где 
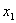 …,
…, 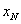 и
и 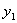 …,
…, 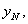 составляющие случайного вектора
составляющие случайного вектора 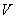 ,
, 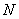 – количество опытов.
– количество опытов.
3.2. Функции случайных аргументов
В практике технологии машиностроения часто приходится определять вероятностные характеристики случайной величины по известным характеристикам распределения других случайных величин, связанных с первой функциональной зависимостью типа:
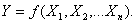
Если функция не линейна, но может быть с достаточной степенью точности линиаризирована (заменена линейной функцией) и приведена к виду:
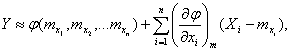
где
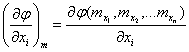
частная производная функция по аргументу хi, в которую вместо каждого аргумента подставлено математическое ожидание, то приближенные характеристики распределения такой функции могут быть вычислены по следующим формулам.
Математическое ожидание
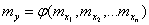 .
.
Дисперсия
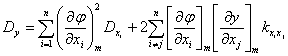 ,
,
где 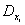 — дисперсия случайной величины
— дисперсия случайной величины 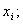
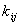 — корреляционный момент величин
— корреляционный момент величин 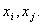
Когда случайные аргументы 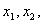 …
… 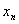 не коррелированны:
не коррелированны:
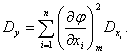
Если функция линейна и представляет собой алгебраическую сумму несвязанных случайных аргументов 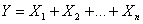 , то ее математической ожидание
, то ее математической ожидание 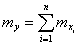 , а дисперсия
, а дисперсия 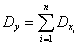 .
.
ЛЕКЦИЯ 4
4. Производственный и технологический процессы
4.1. Свойства и характеристики процесса
Процесс (в широком смысле слова) – последовательные изменения какого-либо предмета (явления) или совокупность последовательных действий, направленных на достижение определенного результата.
Реальный ход процесса, выполняемого машиной, отличается от идеального из-за непрерывно меняющихся условий. Не остаются постоянными во времени качество исходного продукта, количество сообщаемой энергии, изменяется состояние окружающей среды и самой машины, что приводит к нестабильности качества, количества продукции, производимой в единицу времени, и ее стоимости (рис.4.1).
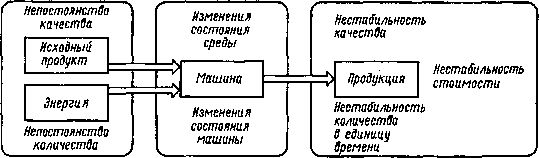
Рис. 4.1. Нарушения намеченного хода процесса
Если в промежутке времени 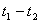 проследить за изменением какой-либо характеристики
проследить за изменением какой-либо характеристики 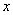 исходного продукта, энергии, состояния внешней среды, количества, качества и стоимости продукта, то можно построить график, подобный представленному на рис.4.2. Для любого другого промежутка времени
исходного продукта, энергии, состояния внешней среды, количества, качества и стоимости продукта, то можно построить график, подобный представленному на рис.4.2. Для любого другого промежутка времени 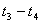 , равного
, равного 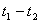 , получился бы график по виду отличный от первого, что на рисунке показано путем наложения второго графика на первый.
, получился бы график по виду отличный от первого, что на рисунке показано путем наложения второго графика на первый.
Таким образом, для любого момента времени 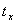 (как и для других моментов) невозможно предсказать значение
(как и для других моментов) невозможно предсказать значение 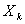 , то есть
, то есть 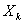 является случайной величиной, а зависимость
является случайной величиной, а зависимость  – случайной функцией.
– случайной функцией.
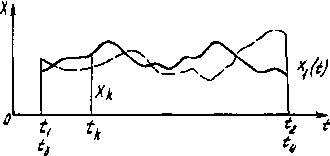
Рис. 4.2. График случайной функции 
Случайной функцией 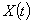 называют такую функцию аргумента
называют такую функцию аргумента 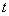 , значение которой при любом значении
, значение которой при любом значении 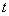 является случайной величиной
является случайной величиной 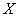 .
.
Роль аргумента на практике часто играет: время, путь, порядковый номер и т.д. Случайную функцию можно рассматривать как бесконечную последовательность значений случайной величины, зависящую от одного или нескольких непрерывно изменяющихся параметров 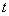 . Каждому значению параметра (параметров) соответствует одно значение
. Каждому значению параметра (параметров) соответствует одно значение 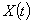 от величины
от величины 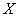 . Все вместе случайные величины
. Все вместе случайные величины 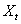 определяют случайную функцию
определяют случайную функцию 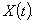 Если аргумент случайной функции может принимать любые значения в заданном интервале, то в этом случае случайную функцию называют случайным процессом. Если же значения аргумента дискретны, то случайную функцию называют случайной последовательностью. Графическое отображение случайной последовательности в технологии машиностроения получило название точечной диаграммы (рис.4.3).
Если аргумент случайной функции может принимать любые значения в заданном интервале, то в этом случае случайную функцию называют случайным процессом. Если же значения аргумента дискретны, то случайную функцию называют случайной последовательностью. Графическое отображение случайной последовательности в технологии машиностроения получило название точечной диаграммы (рис.4.3).

Рис.4.3. Точечная диаграмма обработки деталей на станке
Для характеристик случайной функции при изменении аргумента в области 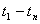 требуется выявить
требуется выявить 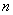 — мерный дифференциальный закон
— мерный дифференциальный закон 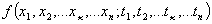 , совместного распределения ее случайных ординат. Существующие способы построения многомерных законов распределения неудобны из-за громоздкости. На практике поэтому пользуются вместо законов их отдельными параметрами. Одним из таких параметров является математическое ожидание.
, совместного распределения ее случайных ординат. Существующие способы построения многомерных законов распределения неудобны из-за громоздкости. На практике поэтому пользуются вместо законов их отдельными параметрами. Одним из таких параметров является математическое ожидание.
Математическим ожиданием случайной функции 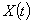 называют такую функцию
называют такую функцию 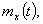 значение которой при каждом данном значении аргумента
значение которой при каждом данном значении аргумента 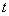 равно математическому ожиданию значения случайной величины
равно математическому ожиданию значения случайной величины 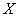 при этом
при этом 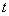 :
:
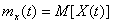
Математическое ожидание случайной функции представляет собой некоторую среднюю функцию, около которой группируются и относительно которой колеблются все возможные реализации случайной функции (рис.4.4):
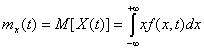 ,
,
где 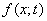 — одномерная плотность вероятности.
— одномерная плотность вероятности.

Рис.4.4. Геометрический смысл математического ожидания
Мерой рассеяния значенияслучайной функции является дисперсия.
Дисперсия случайной функции – функция, значения которой при каждом данном значении аргумента равно дисперсии значений случайной величины 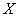 при этом значении аргумента. Дисперсия случайной функции.
при этом значении аргумента. Дисперсия случайной функции.
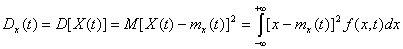 .
.
Математическое ожидание и дисперсия не являются полными характеристиками случайной функции, так как не отражают характер изменения значений случайных ординат во времени. Две случайные функции, имеющие одинаковые 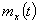 и
и 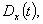 а интенсивность изменения значений случайных ординат у них различна (рис.4.5).
а интенсивность изменения значений случайных ординат у них различна (рис.4.5).
Для того чтобы учесть степень изменчивости случайной функции с изменением аргумента необходимо определить корреляционные связи между парами ее ординат. Корреляционная функция 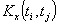 является функцией двух независимых переменных:
является функцией двух независимых переменных:
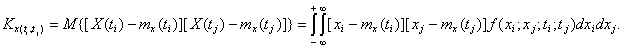
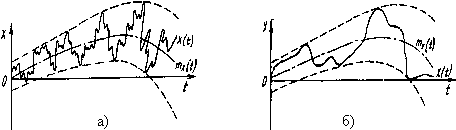
Рис.4.5. Две случайные функции, отличающиеся интенсивностью изменения во времени их ординат
Случайные процессы и последовательности подразделяются на группы по ряду признаков, они могут быть:
· стационарные и нестационарные;
· нормальные и ненормальные;
· марковские и немарковские (в зависимости от поведения случайной функции от ее значений в предшествующий промежуток времени).
Наряду с 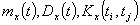 на практике часто рассеяние случайной величины характеризуются величиной
на практике часто рассеяние случайной величины характеризуются величиной 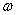 t, называемой мгновенным полем рассеяния. Поле рассеяния случайной величины
t, называемой мгновенным полем рассеяния. Поле рассеяния случайной величины 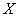 в совокупности случайных величин определяется:
в совокупности случайных величин определяется:
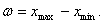
Для зафиксированного момента (мгновения) процесса такой совокупности быть не может, поскольку моменту может соответствовать лишь единственное значение случайной величины X. Однако о пределах, в которых может проявиться это значение, можно судить по разности крайних значений ординат, находящихся поблизости от момента 
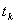 процесса. Это позволяет определить
процесса. Это позволяет определить 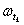 через разность значений таких ординат:
через разность значений таких ординат:
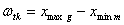
На точечной диаграмме, образующей случайную последовательность, мгновенное поле характеризует ширину полосы точек, в пределах которой наблюдается рассеяние значений 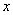 случайных ординат в интервале
случайных ординат в интервале 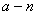 изменения аргумента. Характеристику
изменения аргумента. Характеристику 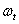 , как и дисперсию случайной функции, следует рассматривать как функцию
, как и дисперсию случайной функции, следует рассматривать как функцию  (рис.4.6).
(рис.4.6).
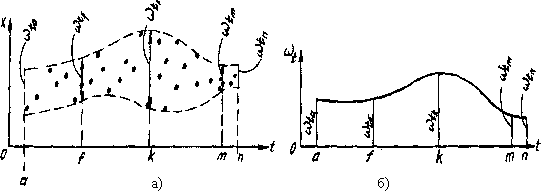
Рис.4.6. Геометрический смысл понятия «мгновенное поле рассеяния»  : а) – точечная диаграмма: б) -
: а) – точечная диаграмма: б) - 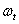 как функция аргумента t
как функция аргумента t
Положение мгновенного поля рассеяния характеризуют либо средним 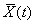 значением случайной функции, либо значением ординат
значением случайной функции, либо значением ординат 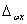 середин мгновенных полей рассеяния.
середин мгновенных полей рассеяния.
Средним значением случайной функции следует считать такую функцию 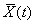 , значения которой равны среднему значению
, значения которой равны среднему значению 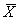 возможных значений случайной величины
возможных значений случайной величины 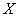 при данном значении аргумента.
при данном значении аргумента.
Существуют различные приемы нахождения 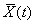 случайной функции. Часто пользуются приемом, основанным на использовании средних групповых значений случайной величины. При этом используется положение теории вероятностей о том, что рассеяние групповых
случайной функции. Часто пользуются приемом, основанным на использовании средних групповых значений случайной величины. При этом используется положение теории вероятностей о том, что рассеяние групповых 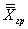 значений случайной величины меньше в
значений случайной величины меньше в 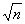 раз рассеяния значений самой случайной величины
раз рассеяния значений самой случайной величины 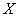 , где
, где 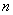 число значений, объединенных в группу:
число значений, объединенных в группу:
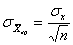
Значения группируются без нарушения последовательности по отношению к аргументу 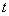 . В каждой группе определяется
. В каждой группе определяется 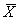 , для представления об
, для представления об 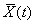 случайной функции, необходимо на средних групповых значениях построить кривую.
случайной функции, необходимо на средних групповых значениях построить кривую.
Другая характеристика положения мгновенного поля рассеяния – ордината 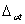 его середины, рассматриваемая как функция аргумента
его середины, рассматриваемая как функция аргумента 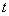 . В примере для момента
. В примере для момента 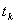 :
:
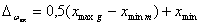
4.2. Понятие о точности
Любой процесс сопровождается действием большого количества случайных факторов, которые вызывают отклонения показателей качества и количества изделий, выпущенных в единицу времени, и их стоимости от стоимости расчетных значений. То есть, между расчетными и действительными результатами процесса всегда бывают расхождения. К тому же,
Дата добавления: 2016-02-20; просмотров: 2148;
