Расчет надежности с учетом постепенных отказов
Экспоненциальный закон надежности, который лежал в основе достаточно простого полного расчета, справедлив лишь в период нормальной эксплуатации, то есть тогда, когда преобладают внезапные отказы и их интенсивность слабо меняется во времени. Однако накапливание мелких количественных изменений в структуре проводников, изоляторов и полупроводниковых материалов приводит к появлению деградационных (постепенных) отказов, количество которых постоянно возрастает. В период интенсивного старения постепенные отказы становятся преобладающими.
Чтобы учесть при расчете надежности не только внезапные, но и постепенные отказы, необходимо знать закон распределения времени исправной работы элементов относительно постепенных отказов и его характеристики.
Опыт показывает, что распределение времени исправной работы относительно постепенных отказов близко к нормальному. На рис. 2.4 изображена плотность этого распределения с параметрами:
 ‑ среднее время исправной работы элемента относительно только постепенных отказов;
‑ среднее время исправной работы элемента относительно только постепенных отказов;
δ ‑ среднеквадратическое отклонение этого распределения.
Рис. 2.4. Плотность распределения постепенных отказов
Вероятность появление постепенного отказа элемента в течение некоторого интервала времени [0,t1] может быть определена как вероятность попадания случайной величина tx (момента появления постепенного отказа) в заданный интервал [0,t1].
Напомним, что вероятность попадания случайной величины на заданный участок [a,b]b определяется разностью
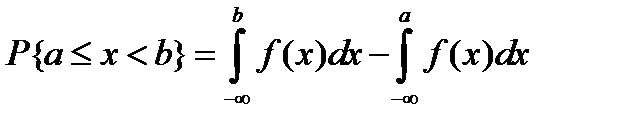
где f(x) ‑ плотность распределения случайной величины x .
На рис. 2.5 представлено некоторое распределение с плотностью f(x), характеризующееся параметрами mx (математическое ожидание) и δx (среднеквадратическое отклонение).
Рис.2.5. Плотность распределения случайной величины x
Плотность вероятности нормального распределения имеет вид:
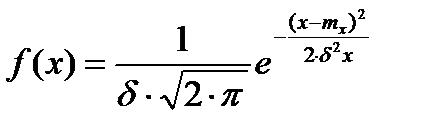
Интеграл от функции такого вида не берется, и для определения P{a≤x<b}пользуются табулированными функциями Лапласа:
 ,
,
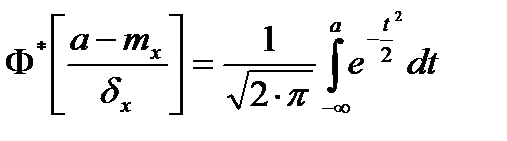 ,
,
где 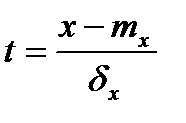 ,
, 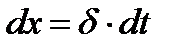
Учитывая, что в интервале длиной 6δ (±3δ); укладывается 0,997 площади под кривой ƒ(x) плотности нормального распределения; полезно запомнить соотношения площадей, показанные на рис. 2.6.
Рис.2.6. Соотношения площадей под кривой плотности нормального распределения
Вероятность 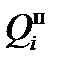 появления постепенного отказа элемента в период [0,t1] есть ничто иное, как
появления постепенного отказа элемента в период [0,t1] есть ничто иное, как
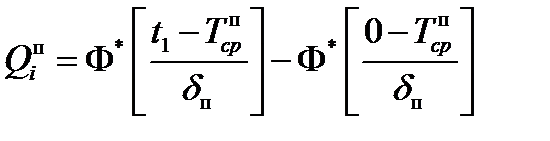
Тогда вероятность исправной работы одного элемента относительно постепенных отказов в этот же период равна
| (8) |
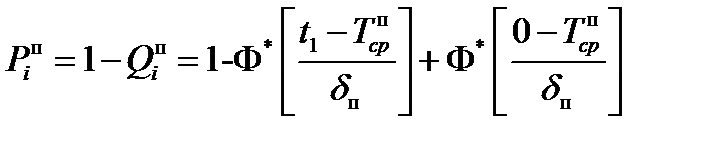
Если имеется радиоэлектронная система, состоящая из N однотипных элементов, соединенных в смысле надежности последовательно, то вероятность ее исправной работы относительно постепенных отказов равна произведению 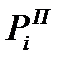 . Считая постепенные отказы элементов независимыми событиями, получим
. Считая постепенные отказы элементов независимыми событиями, получим
| (9) |

Например: система состоит из N=10 равнонадежных элементов, у которых распределение постепенных отказов является нормальным с параметрами 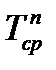 = 3 тыс. часов и δп= 1,5 тыс. часов. Определить вероятность исправной работы системы относительно постепенных отказов в течение периода эксплуатации, равного 5 тыс. часов.
= 3 тыс. часов и δп= 1,5 тыс. часов. Определить вероятность исправной работы системы относительно постепенных отказов в течение периода эксплуатации, равного 5 тыс. часов.
Используя формулу (9), получаем
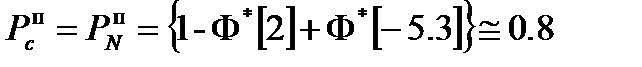
| (10) |

где 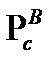 - вероятность исправной работы системы на N элементов относительно внезапных отказов.
- вероятность исправной работы системы на N элементов относительно внезапных отказов.
Учитывая (3) и (9), получаем
| (11) |
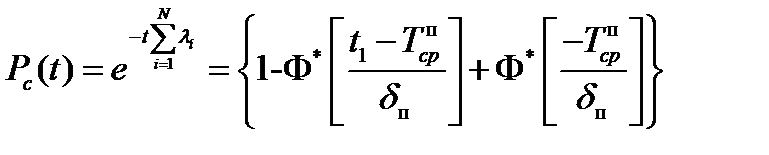
Последняя формула справедлива для двух периодов работы элементов: периода нормальной эксплуатации и периода интенсивного старения. При этом предполагается, что период приработки элементов пройдет во время предварительной заводской тренировки.
Дата добавления: 2016-02-20; просмотров: 1681;
