Оптимизация параметров РЭА по критерию надежности
Как уже было показано выше (10), вероятность безотказной работы радиоэлектронных устройств и систем может быть определена как вероятность отсутствия внезапных и постепенных отказов. Отсюда видна роль улучшения надежности по постепенным отказам в общем балансе увеличения суммарной надежности изделий. Одним из важнейших способов обеспечения надежности устройств является оптимизация их параметров по критерию надежности с учетом многих выходных параметров.
При решении задачи оптимизации параметров РЭА [5-7] возникает ряд вопросов:
· выбор формы выражения критерия надежности;
· составление моделей работоспособности отдельных компонентов,
· анализ функционирования разрабатываемого объекта в. поле допуска;
· анализ чувствительности;
· выбор метода экстремизации и др.
Сложность задачи оптимизации определяется рядом факторов. Главными из них являются необходимость вероятностного анализа по всем аспектам, а также отсутствие достоверных моделей поведения параметров элементов радиоаппаратуры во всех условиях эксплуатации.
Важность выбора в качестве критерия оптимизации такого показателя, как надежность, определяется, прежде всего, тем, что надежность - это обобщающий показатель качества функционирования радиоаппаратуры.
Кроме того, увеличение стабильности, уменьшение различного рода ошибок косвенно приводит к уменьшению сложности аппаратуры, повышению ее экономичности по питанию, уменьшению массы и габаритов. Объясняется этот эффект тем, что при больших ошибках и малой стабильности выходных параметров стыкуемых блоков и узлов в РЭА приходится вводить в этих блоках большие запасы (избыточность) по выходной мощности, напряжению питания, чувствительности в т.д. Введение запасов необходимо для обеспечения надежности срабатывания "запускаемого" блока при больших ошибках его напряжения запуска или нестабильности выходного напряжения "запускающего" блока. Уменьшение ошибок дает возможность уменьшить эти запасы, а, следовательно, сократить избыточность.
Критерий надежности математически может быть выражен только при наличии соответствующих моделей компонентов, а также при возможности анализа функционирования объекта с учетом вероятностных характеристик. Оба эти вопроса достаточно сложны в решении.
Случайные изменения параметров компонентов отражают два вида происходящих в них процессов [1-4]: долговременные и кратковременные. Долговременные процессы отражают те основные физико-химические изменения, которые характеризуют сущность исследуемого компонента. Кратковременные процессы свидетельствуют о локальных явлениях (как в объеме, так и по времени), в том числа о шуме измерений. Оба эти вида процессов изучены недостаточно (особенно кратковременные). Поэтому весьма ограничены возможности моделирования параметров в условиях действия возмущающих факторов - производственного разброса, температуры, старения, радиационных воздействий и т.д. Практически нет сведений о влиянии возмущающих факторов на поток внезапных отказов. Основной причиной этих трудностей является то, что собираемые сведения о конкретных элементах очень быстро (2-3 года) делаются непригодными из-за морального устаревания материалов и изделий (изменение технологии производства, смена элементной базы - замена более современными изделиями и т.д.).
В связи с этим становятся необходимым выявление общих закономерностей, справедливых практически во всех случаях. Такими закономерностями могут быть:
· законы изменения числовых характеристик распределений;
· характер изменения корреляционной функции;
· - законы распределения случайных величин и т.д.
Законы распределения случайных величин ошибок обычно принимаются нормальными. Также практически однозначно определен характер изменения корреляционной функции. Ее нормированное значение
| (12) |
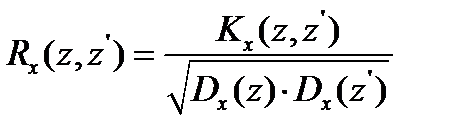
где 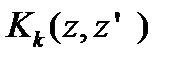 - корреляционная функция,
- корреляционная функция,
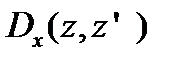 - дисперсия в разных сечениях случайного процесса.
- дисперсия в разных сечениях случайного процесса.
монотонно убывает от единицы до трех-четырех десятых через тысячу часов. Что касается изменения числовых характеристик - математического ожидания и дисперсия, в большинстве случаев их изменение принимают линейными со временем, хотя и имеются сведения о нелинейном виде функций – экспоненциальном, степенном и др. Соответственно строятся математические модели случайных процессов. Чаще всего модели представляются в виде веерных случайных процессов, хотя в этом случае корреляционная функция Rx тождественно равна единице. Обычно предлагается использовать модель случайного процесса в виде дробно-рациональной функции [6]
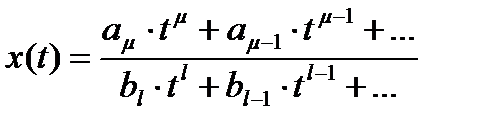
хотя, как ясно из сказанного, информация для определения коэффициента a и b весьма мала. Другие способы основаны на апостериорной аппроксимации характеристик случайных процессов.
В связи с этим наиболее справедливым представляется выражение случайных процессов в виде композиции веерных случайных функций
| (13) |
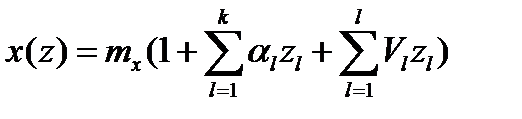
где mx - математическое ожидание параметра X;
zl - возмущающее воздействие, l=1,2…k;
αl- коэффициент изменения систематической ошибки параметра;
Vl - число, характеризующее случайную ошибку параметра.
Модель (13) обеспечивает монотонное уменьшение нормированной корреляционной функции (12), а ее числовые характеристики легко определяются по данным технических условий на элементы РЭА. Коэффициенты αl - это коэффициенты изменчивости параметра при соответствующих воздействиях - тепловом, старении, влажности и т.д. Среднеквадратическая ошибка числа Vl также непосредственно определяется из технических условий - она равна одной трети случайной ошибки при воздействии zl.
Другим достоинством модели (13) является то, что оценка ее среднеквадратической ошибки растет во времени и скорость этого роста может регулироваться подбором коэффициентов. При этом изменение дисперсии может быть получено нелинейным во времени, что соответствует реальным изменениям в компонентах радиоэлектронных устройств в процессе их эксплуатации.
Вид модели (13) показывает, что в ней легко может быть реализованы различные законы (функции) изменения систематической и случайных ошибок, а также смоделированы кратковременные случайные процессы путем добавления еще одного слагаемого случайной величины. Главным же достоинством приведенной модели является то, что в ней применена композиция случайных функций, что соответствует основной идее координатного разложения случайных процессов и позволяет обеспечить выполнение всех без исключения общих закономерностей изменения параметров реальных компонентов.
Анализ функционирования проектируемого изделия в поле допуска выходных параметров может производиться различными способами. Чаще всего для этого используется метод числовых характеристик
| (14) |
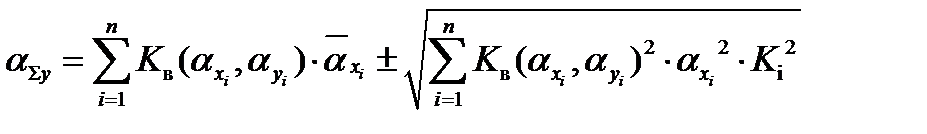
где 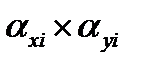 - относительные ошибки первичного и выходного параметров;
- относительные ошибки первичного и выходного параметров; 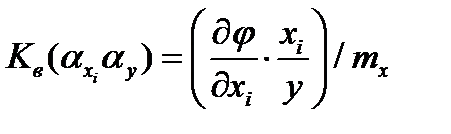 - коэффициент влияния.
- коэффициент влияния.
Применение других методов затруднено из-за возрастания количества вычислений значений выходных параметров. Это относятся как к использованию различного рода полиномов (Эрмита, Уолта и др.), так и применению метода статистических испытаний. Все эти приемы обеспечивают увеличение точности расчета ошибок выходных параметров за счет непропорционально большого увеличения сложности. Более того, сами расчеты могут иметь погрешности до десятков процентов. Единственно, чем можно оправдать увеличение сложности расчетов, так это стремлением определить закон распределения ошибки выходного параметра. Выражение (14) на этот вопрос дает один ответ - закон приближается к нормальному. Точнее, (14) составлено в предположении справедливости нормального закона для выходного параметра. Хотя в редких случаях это несправедливо.
В то же время определенную сложность в методе числовых характеристик представляет определение коэффициентов влияния (анализ чувствительности).
В настоящее время при анализе радиоэлектронных устройств применяется несколько методов анализа чувствительности:
· метод приращений;
· метод присоединенной схемы;
· метод дифференцирования уравнений и некоторые другие.
Наиболее универсальным является метод приращений. Особенно удобен этот метод, когда модель схемы представлена в виде полинома или дробнорационального выражения.
При машинном анализе чаще используются другие два метода. Они требуют, прежде всего, лишь двукратного увеличения числа расчетов.
Недостатком этих методов является то, что с их помощью определяется чувствительность только для переменных схемы - токов, напряжений, то есть величины 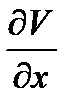 . Для частотных и временных характеристик - граничных частот, различного рода задержек чувствительность все равно приходится определять методом приращений.
. Для частотных и временных характеристик - граничных частот, различного рода задержек чувствительность все равно приходится определять методом приращений.
Таким образом, вероятностный анализ радиоэлектронных устройств наиболее удобен при их моделировании в виде явных функций, а не в виде систем дифференциальных уравнений. Кроме того, явные функции построены для значимых параметров, для которых и нужно определять чувствительность, в то время как метод присоединенной схемы дает чувствительность для всех элементов.
Следующим этапом является математическое выражение критерия надежности в виде целевой функции. В простейшем виде это может быть записано 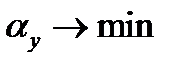 при
при  ,
,
где 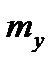 и
и 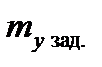 - текущее и заданное значения выходного параметра.
- текущее и заданное значения выходного параметра.
Более строгое выражение для целевой функции может быть получено с помощью, так называемых запасов работоспособности. Запасы работоспособности могут измеряться от верхней или нижней границы поля допуска (ТТВ, ТТН) до среднего my верхнего или нижнего граничного значения (yг) выходного параметра.
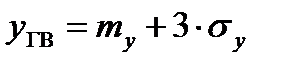 ;
; 
| (15) |
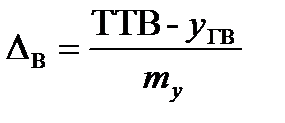 ;
; 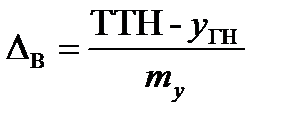
где ∆В, ∆Н - верхний и нижний запасы работоспособности.
Запасы работоспособности могут определяться для любого момента времени в соответствии с изменением ошибки модели (13).
При реализации следующего этапа оптимизации - экстремизации необходимо обеспечить максимум всех запасов работоспособности по воем границам, по всем выходным параметрам.
Модель (13) позволяет использовать еще одну форму критерия надежности - критерий долговечности. Если в (13) выделить те ошибки, которые появляются с течением времени Zt , то уравнения для математического ожидания и ошибки выходного параметра (14) примет вид:
| (16) |
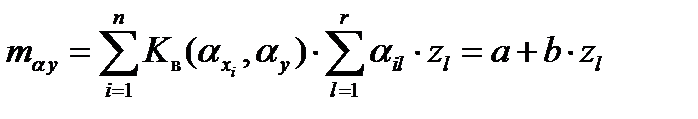
где
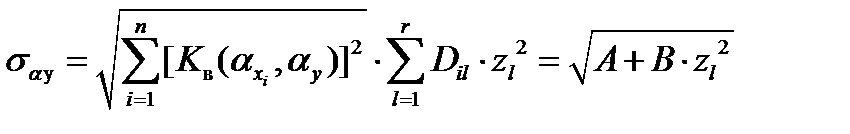
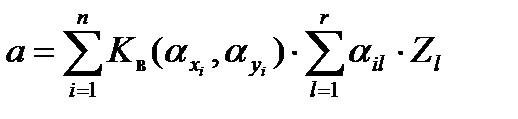
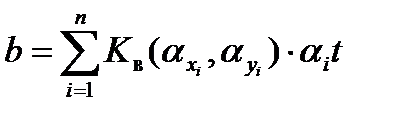

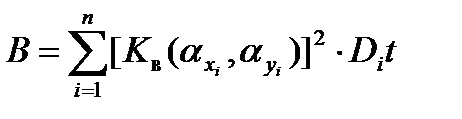
Очевидно, что величины αit и Dit должны учитывать все ошибки (систематические и случайные), которые накапливаются со временем.
Из (16) видно, что среднеквадратическая ошибка выходного параметра со временем растет по гиперболе. Поэтому граничные значения (15) рано или поздно пересекут границы поля допуска ТТН или, ТТБ (конечно, если первоначально значения yг находились в поле допуска), Моменты времени нарушения технических требований и принимаются за критерий оптимизации
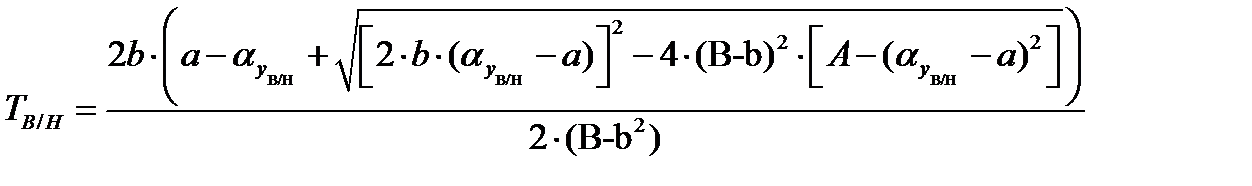
где
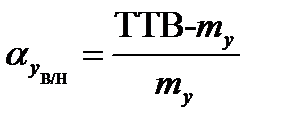
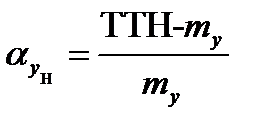
Критерии (15) или (17) сводятся в интегральный критерий, например:
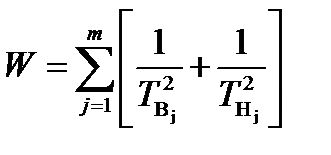
где объединяются частные критерии для всех m выходных параметров. В (18) для каждого выходного параметра можно использовать свой весовой коэффициент (в частном случае равные единице). Как в критерии запасов работоспособности, так и в критерии долговечности можно учесть отличие закона распределения выходного параметра от нормального - введением коэффициентов формы Ki (14).
Методы поиска экстремума, применяемые при оптимизации, должны отвечать определенным требованиям:
· обеспечивать использование различных критериев оптимизации целевых функций;
· решать многоэкстремальные задачи;
· учитывать различного рода ограничения;
· решать многокритериальные задачи;
· работать с овражными целевыми функциями оптимизации и т.д. При выборе метода поиска экстремума кроме перечисленных необходимо учитывать следующее:
· скорость сходимости итерационного процесса поиска;
· количество вычислений оптимизируемой функции;
· неявное задание целевой функции и т.д.
Все эти факторы в конечном итоге определяют затрачиваемое на оптимизацию время и достоверность результатов.
Время, затрачиваемое на поиск оптимума, определяется как
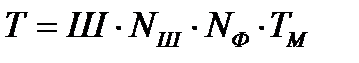
где Tm - затрата времени на одновариантный анализ, то есть на однократное вычисление значения выходного параметра;
Nф - количество расчетов вариантов для однократного вычисления целевой функции;
Nш - среднее количество вычислений целевой функции на один шаг поиска;
Ш - количество шагов поиска.
В качестве метода поиска экстремума могут быть выбраны или простые метода, не требующие вычисления градиента, или методы первого порядка [8]. В любом случае следует ориентироваться на алгоритмы, эффективно работавшие с овражными (гребневыми) целевыми функциями. Среди простых можно рекомендовать методы Пауэлла, Розенброка, случайного поиска и комплекс-метод. Среди методов первого порядка - метод Флетчера-Пауэлла, метод прослеживания оврага и другие.
Опыт работы с большинством из перечисленных методов показывает, что вычисление градиента при "глубоких" оврагах целевой функции производится с большими ошибками. Не спасает положения введение сложных разностных схем, поскольку влияние ошибки округления остается достаточно большим. Некоторым выходом из этой трудной ситуации является введение двойной точности счета. Но при этом резко возрастают затраты времени. Кроме того, градиентные методы оказываются очень чувствительны к числу параметров. Даже небольшое увеличение числа параметров n приводит к ухудшению работоспособности методов, замедлению сходимости и увеличению затрат времени. Это объясняется тем, что с возрастанием n- увеличивается как число расчетов выходного параметра, так и число вычислений Nш, то есть затраты времени растут пропорционально квадрату n. Кроме того, при увеличении числа параметров, как правило, усиливаются диспропорции между ними, что также ухудшает эффективность поиска. Введение нормировки полностью этого недостатка не устраняет.
Среди простых методов следует выделить комплекс-метод [8]. Этот метод в наибольшей мере отвечает перечисленным выше требованиям как в смысле универсальности и учета ограничений, так и в смысле поиска глобального экстремума исследуемого критерия. Важным достоинством комплекс-метода является незначительное увеличение вычислительной сложности при увеличении числа параметров n.
Таким образом, при схемотехническом проектировании высоконадежной РЭА целесообразно использовать косвенные выражения критерия надежности, позволяющие проводить оптимизацию параметров РЭА при практически незначительных затратах машинного времени. При этом оценку точности результатов оптимизации можно осуществлять методой статистических испытаний - сравнив рассеяние выходных параметров до и после проведения экстремизации. Применение метода статистических испытаний на математической модели схемы, составленной в виде полинома или дробно-рационального выражения, не потребует больших затрат времени.
Дата добавления: 2016-02-20; просмотров: 1415;
