Результирующий механический момент многоэлектронного атома
При образовании в результате сложения спиновых 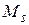 и орбитальных
и орбитальных 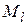 моментов импульса электронов результирующего момента атома
моментов импульса электронов результирующего момента атома 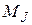 возможны два случая:
возможны два случая:
1. магнитное взаимодействие орбитальных моментов 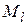 различных электронов сильнее, чем их взаимодействие со спиновыми моментами
различных электронов сильнее, чем их взаимодействие со спиновыми моментами 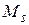 . Аналогично спиновые моменты связаны между собою сильнее, чем с орбитальными. В результате сначала образуются результирующие орбитальный
. Аналогично спиновые моменты связаны между собою сильнее, чем с орбитальными. В результате сначала образуются результирующие орбитальный 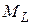 и спиновой
и спиновой 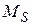 моменты импульса, которые затем складываются между собой и образуют
моменты импульса, которые затем складываются между собой и образуют 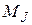 . Такая связь называется LS-связью или Рёссель-Саундерсовской и встречается наиболее часто.
. Такая связь называется LS-связью или Рёссель-Саундерсовской и встречается наиболее часто.
2. У ряда тяжелых атомов 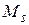 и
и 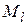 каждого электрона взаимодействуют между собой сильнее, чем с моментами других электронов. Поэтому сначала образуются результирующие
каждого электрона взаимодействуют между собой сильнее, чем с моментами других электронов. Поэтому сначала образуются результирующие 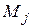 отдельных электронов, а потом
отдельных электронов, а потом 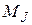 всего атома. Это случай j j-связи.
всего атома. Это случай j j-связи.
В случае LS-связи, поскольку орбитальные квантовые числа отдельных электронов 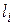 всегда целые, квантовое число L результирующего орбитального момента также всегда целое.
всегда целые, квантовое число L результирующего орбитального момента также всегда целое.
Квантовое число S результирующего спинового момента атома 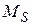 может быть целым или полуцелым в зависимости от числа электронов в атоме: четное-нечетное.
может быть целым или полуцелым в зависимости от числа электронов в атоме: четное-нечетное.
При данных L и S квантовое число результирующего момента J может иметь значения
J = L + S, L+S-1,…| L- S|,. (36.10)
т.е. может быть и целым и полуцелым.
Энергия атома зависит от взаимной ориентации орбитальных моментов отдельных электронов 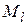 - квантового числа L , взаимной ориентации спиновых моментов электронов - квантового числа S и взаимной ориентации результирующих моментов квантового числа J.
- квантового числа L , взаимной ориентации спиновых моментов электронов - квантового числа S и взаимной ориентации результирующих моментов квантового числа J.
Термы многоэлектронных атомов обозначают аналогично термам щелочных металлов символами 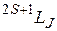 . Такое обозначение удобно тем, что содержит в себе сведения о значениях трех квантовых чисел: S, L, J. Если S < L, стоящее слева вверху число 2S + 1 дает мультиплетность терма, как и в случае щелочных металлов. Если S > L, то фактическая мультиплетность равна 2L + 1, однако символ терма не изменяют, чтобы была возможность указать значение квантового числа S.
. Такое обозначение удобно тем, что содержит в себе сведения о значениях трех квантовых чисел: S, L, J. Если S < L, стоящее слева вверху число 2S + 1 дает мультиплетность терма, как и в случае щелочных металлов. Если S > L, то фактическая мультиплетность равна 2L + 1, однако символ терма не изменяют, чтобы была возможность указать значение квантового числа S.
Дата добавления: 2016-02-11; просмотров: 1249;
