Групповая скорость в диспергирующей среде
Получим аналитическое выражение для групповой скорости. Для упрощения рассуждений и математических выкладок, рассмотрим суперпозицию всего лишь двух плоских волн, и будем считать, опять же для простоты, что их амплитуды одинаковы, а начальные фазы равны нулю. Уравнения волн имеют вид:
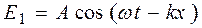 ,
, 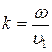 (30.5)
(30.5)
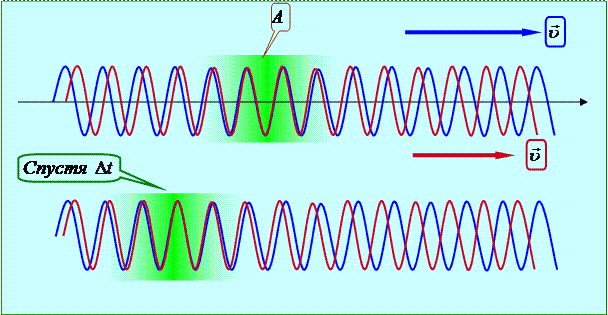 |
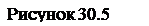
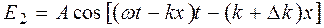 ,
, 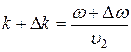 (30.6)
(30.6)
Графически наложение волн можно представить так, как показано на рисунке 30.5. Интенсивность суммарной волны очевидно будет максимально в окрестности точки А, в которой колебания волн происходят в одной фазе.
Допустим, что обе волны перемещаются слева направо и скорость «красной» волны меньше, чем «синей». Поскольку у «красной» волны длина волны меньше, то в рассматриваемом случае 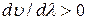 , а
, а 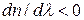 (поскольку
(поскольку 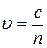 , положительному
, положительному 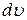 соответствует отрицательное приращение
соответствует отрицательное приращение 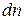 ). Условие
). Условие 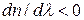 соответствует нормальной дисперсии.
соответствует нормальной дисперсии.
С течением времени «синяя» волна догоняет «красную» и точка А будет перемещаться влево относительно волн. Соответственно групповая скорость в данном случае будет меньше фазовой.
При обратном соотношении между скоростями, т. е. если скорость длинноволновой составляющей меньше, чем у коротковолновой, место усиления колебаний будет перемещаться вдоль направления распространения и групповая скорость будет больше фазовой. Такая ситуация соответствует аномальной дисперсии.
Уравнение результирующей волны получим, сложив (30.5) и (30.6):
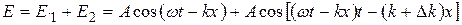 . (30.6)
. (30.6)
По формуле суммы косинусов получаем:
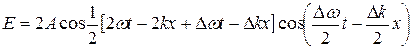 (30.7)
(30.7)
Учитывая, что 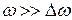 и
и 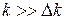 , получаем:
, получаем:
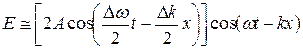 (30.8)
(30.8)
В уравнении (30.8) первый косинус изменяется гораздо медленнее, чем второй. Поэтому (30.8) можно рассматривать как уравнение плоской волны, с амплитудой, медленно изменяющейся с течением времени и увеличением координаты:
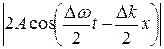 (30.9)
(30.9)
Поскольку мы рассматриваем наложение только двух волн, то в нашем случае имеется ряд одинаковых максимумов амплитуды, которые, в соответствии с (30.9) определяются условием:
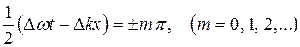 (30.10)
(30.10)
Отсюда находим координаты максимумов:
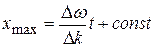 ;
; 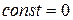 при
при 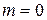 . (30.11)
. (30.11)
Скорость перемещения центра рассматриваемой «группы волн»
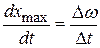 . (30.12)
. (30.12)
Таким образом, максимум амплитуды результирующей волны перемещается со скоростью
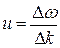 . (30.13)
. (30.13)
Переходя к дифференциалам для групповой скорости находим:
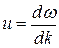 . (30.14)
. (30.14)
Поскольку 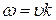 , то из (30.14) следует
, то из (30.14) следует
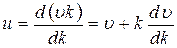 . (30.15)
. (30.15)
Производную 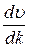 можно представить в виде:
можно представить в виде:
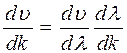 . (30.16)
. (30.16)
По определению волнового вектора
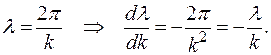 (30.17)
(30.17)
Подставим это значение 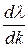 в (30.16):
в (30.16):
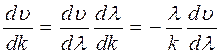 . (30.18)
. (30.18)
Это значение в свою очередь подставим в (30.15)
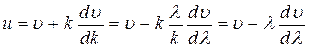 . (30.19)
. (30.19)
Поэтому для групповой скорости справедливо соотношение:
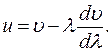 (30.20)
(30.20)
Как видно из (30.20), в зависимости от знака 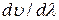 групповая скорость может быть и меньше и больше фазовой. В отсутствии дисперсии
групповая скорость может быть и меньше и больше фазовой. В отсутствии дисперсии 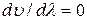 и групповая скорость совпадает с фазовой.
и групповая скорость совпадает с фазовой.
Следует иметь в виду, что само понятие групповой скорости имеет смысл только в том случае, если поглощение энергии волны в данной среде не слишком велико. При значительном затухании, например в области аномальной дисперсии, поглощение велико, понятие групповой неприменимо. Физически это означает, что волновой пакет при этом быстро расплывается в пространстве.
Дата добавления: 2016-02-11; просмотров: 1525;
