Закономерности в атомных спектрах
 |
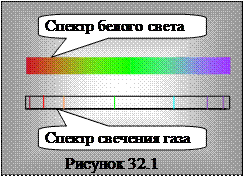Если при исследовании дисперсии по методу скрещенных призм (рисунок 30.1) на первую призму направить пучок не белого света, а свет, полученный при излучении молекулами некоторого газа, то вместо сплошного спектра наблюдаются отдельные линии (рисунок 32.1). Экспериментально установлено, что подобные спектры характерны для всех атомов, если при излучении вещество находится в газообразном состоянии и взаимодействием между атомами можно пренебречь. Такие спектры называется линейчатыми.
Реальные спектры (в отличии от показанного на рисунке) содержат заметно большее количество линий. Линии испускания в спектрах атомов упорядочены и объединяются в серии линий, частоты которых описываются определенным соотношением.
Рассмотрим подробнее спектр испускания самого простого атома – атома водорода.
Частоты всех линий спектра атома водорода можно представить одной формулой:
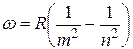(32.1)
где R = 2,07 1016рад/с – постоянная Ридберга.
m, n – целые числа,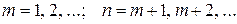 
Формула (32.1) называется обобщенной формулой Бальмера. Каждой серии линий в спектре водорода соответствует свое число m. При заданном m число n принимает все целочисленные значения, начиная с m + 1. Частота каждой серии стремится к предельному значению R/m2 ,которое называется границей серии.
В атоме водорода первым сериям даны имена по имени ученого, установившего существование соответствующей линии:
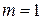– cерия Леймана;
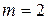– cерия Бальмера;
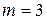– cерия Пашена;
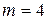– cерия Брекета;
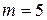– cерия Пфунда.
Рассмотрим ряд значений функции:
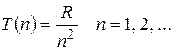(32.2)
Легко видеть, что частота любой линии спектра водорода может быть представлена в виде разности чисел ряда (32.2) .Числа этого ряда называют спектральными термами. Можно говорить, что частота лини равна разности спектральных термов.
Спектры других атомов похожи на спектр водорода, частоты линий также могут быть представлены в виде разностей двух термов:
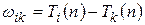, (32.3)
однако термы имеют более сложный вид, и члены (32.3) берутся, вообще говоря, из различных рядов.
Дата добавления: 2016-02-11; просмотров: 1325;