Равновесная плотность энергии излучения.

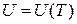Рассмотрим излучение, находящееся в равновесии с веществом. Такое излучение будет существовать в вакууммированной полости, стенки которой поддерживаются при температуре Т. Энергия излучения распределена в объеме с определенной плотностью . Спектральное распределение энергии в полости можно охарактеризовать функцией 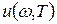, такой, что плотность энергии 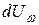в интервале частот от 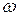до 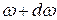определяется соотношением:

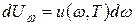. (31.12)

На основе законов термодинамики можно доказать, что плотность энергии излучения зависит только от температуры, и не зависит от других свойств стенок полости.

Действительно, представим себе что имеются две полости из разных материалов, но с одинаковой температурой Т. Будем рассуждать методом «от противного». Допустим, что плотности энергии в полостях неодинаковы: 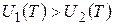. Соединим полости небольшим отверстием. Поток энергии из певой полости во вторую будет больше. Это приведет к тому, что плотность энергии в первой полости уменьшится и ее стены будут больше излучать энергии, чем поглощать. Тогда стенки первой полости начнут охлаждаться. Во второй полости ситуация противоположная, и ее полости начнут нагреваться. В результате мы получим два тела, которые первоначально имели одинаковую температуру, а в результате теплообмена между ними, их температуры стали различными. Такие процессы запрещены вторым началом термодинамики, а значит исходное предположэение неверно и 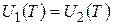независимо от материала, из которго изготовлены стенки полостей.

Равновесная плотность энергии излучения 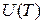внутри полости с абсолютно черными стенками связана с энергетической светимостью абсолютно черного тела 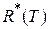. Если бы излучение с плотностью энергии 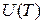представляло собой направленный поток электромагнитных волн, то вектор Пойтнинга , характеризующий плотность потока энергии волн, можно было бы найти как произведение 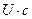. Однако в полости у излучения присутствуют все направления движения. Поэтому поток энергии 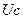равномерно распределен в пределах телесного угла 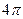. Соответственно, через каждую точку полости в любом направлении в пределах телесного угла 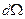распространяется поток с плотностью

. (31.13)

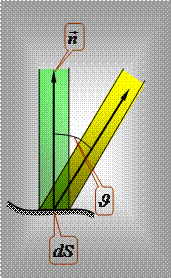
Площадка 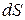поверхности полости посылает в направлении перпендикуляра к ней 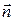поток энергии 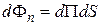. В направлении, составляющем с нормалью угол 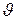, поток энергии будет равен:

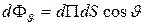(31.14)

Учтем, что 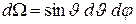и подставив выражение для 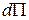в (31.14) получим:

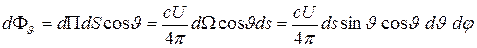. (31.15)

Для того, чтобы получить полный поток энергии от элемента 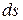по всем направлениям, другими словами в пределах телесного угла 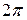, необходимо проинтегрировать (31.15) в пределах от 0 до 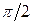по углу 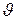, и в пределах от 0 до 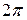по углу :

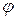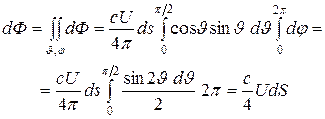(31.16)

С другой стороны, в соответствии с определением энергетической светимости, поток энергии, испускаемый 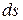, может быть представлен в виде:

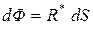(31.17)

Сравнивая (31.16) и (31.17) находим:

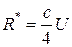. (31.18)

Это соотношение должно выполнятся для каждой спектральной составляющей излучения. Поэтому для испускательной способности абсолютно черного тела должно быть справедливо:

. (31.19)