Энергия упругой волны
Рассмотрим в среде, в которой распространяется упругая волна (22.10), 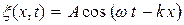 элементарный объём
элементарный объём 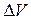 достаточно малый, чтобы деформацию и скорость движения частиц в нём можно было считать постоянными и равными:
достаточно малый, чтобы деформацию и скорость движения частиц в нём можно было считать постоянными и равными:
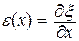 и
и 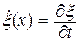 . (22.37)
. (22.37)
Вследствие распространения в среде волны объём 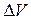 обладает энергией упругой деформации
обладает энергией упругой деформации
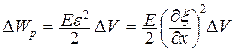 (22.38)
(22.38)
В соответствии с (22.35) модуль Юнга можно представить в виде 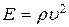 . Поэтому:
. Поэтому:
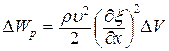 . (22.39)
. (22.39)
Рассматриваемый объём обладает также кинетической энергией:
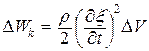 . (22.40)
. (22.40)
Полная энергия объёма:
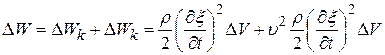 . (22.41)
. (22.41)
А плотность энергии:
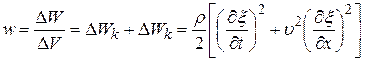 . (22.42)
. (22.42)
Но
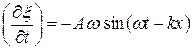 , а
, а 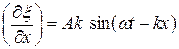 (22.43)
(22.43)
Подставим эти выражения в (22.42) и учтем, что 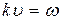 :
:
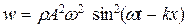 . (22.44)
. (22.44)
Таким образом, плотность энергии различна в разных точках пространства и меняется во времени по закону квадрата синуса.
Среднее значение квадрата синуса равно 1/2, а значит среднее по времени значение плотности энергии в каждой точке среды, в которой распространяется волна:
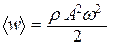 . (22.45)
. (22.45)
Выражение (22.45) справедливо для всех видов волн.
Итак, среда, в которой распространяется волна, обладает дополнительным запасом энергии. Следовательно, волна переносит с собой энергию.
Дата добавления: 2016-02-11; просмотров: 697;
