Плоская электромагнитная волна
Для того, чтобы представить структуру электрического и магнитного полей в электромагнитной волне, исследуем с помощью уравнений Максвелла простейшую – плоскую электромагнитную волну.
Направим ось Ох перпендикулярно волновым поверхностям. Тогда векторы 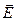
и 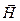 , а значит и их компоненты, не будут зависеть от координат z и y. Поэтому производные от векторов поля по этим координатам равны нулю. С учетом этого запишем уравнение Максвелла (22.2)
, а значит и их компоненты, не будут зависеть от координат z и y. Поэтому производные от векторов поля по этим координатам равны нулю. С учетом этого запишем уравнение Максвелла (22.2) 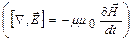 в проекциях на оси координат:
в проекциях на оси координат:
на ось Ох 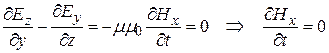 ; (22.13)
; (22.13)
на ось Оу  (22.14)
(22.14)
на ось Оz 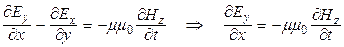 ; (22.15)
; (22.15)
Уравнение (22.4) 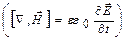 в проекциях на оси координат дает следующие три соотношения:
в проекциях на оси координат дает следующие три соотношения:
на ось Ох  ; (22.16)
; (22.16)
на ось Оу  (22.17)
(22.17)
на ось Оz 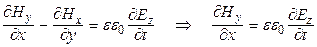 ; (22.18)
; (22.18)
Из уравнения (22.5) 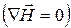 следует:
следует:
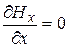 , (22.19)
, (22.19)
а из уравнения (22.3) 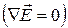 -
-
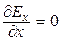 (22.20)
(22.20)
Соотношения (22.13) 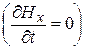 и (22.19)
и (22.19) 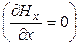 показывают, что составляющая
показывают, что составляющая 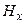 не зависит ни от х, ни от
не зависит ни от х, ни от  . Аналогично соотношения (22.16) и (22.20) указывают на независимость от х и
. Аналогично соотношения (22.16) и (22.20) указывают на независимость от х и  составляющей поля волны
составляющей поля волны  . Поэтому ненулевые составляющие
. Поэтому ненулевые составляющие  и
и 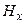 могут быть только постоянными во времени однородными полями. Но к электромагнитной волне, в которой переменные во времени и пространстве составляющие порождают друг друга, постоянные поля не могут иметь никакого отношения и могут быть только некими внешними полями. Следовательно, в плоской электромагнитной волне составляющие
могут быть только постоянными во времени однородными полями. Но к электромагнитной волне, в которой переменные во времени и пространстве составляющие порождают друг друга, постоянные поля не могут иметь никакого отношения и могут быть только некими внешними полями. Следовательно, в плоской электромагнитной волне составляющие  и
и 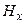 равны нулю, а значит, она является поперечной. Поперечность в данном случае означает, что в плоской ЭМВ
равны нулю, а значит, она является поперечной. Поперечность в данном случае означает, что в плоской ЭМВ
Для дальнейшего анализа объединим в пары уравнения (22.15), (22.17) и (22.14), (22.18) в соответствии с составляющими, которые они связывают:
 , (22.21)
, (22.21)
 (22.22)
(22.22)
Допустим, что в начальный момент было создано электрическое поле вдоль оси Оу -  . Из (22.21) следует, что это поле порождает е67апнаеакмагнитное поле направленное
. Из (22.21) следует, что это поле порождает е67апнаеакмагнитное поле направленное 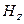 по оси Oz, которое, в свою очередь, может создать электрическое поле только вдоль оси Оу. Составляющие полей из уравнений (22.22) при этом возникнуть не могут. Аналогиччная ситуация имеет место и для уравнений (22.22). Забегая вперед, отметим, что указанная особенность соотношений (22.21) и (22.22) отражает тот факт, что каждая из пар соответствует независимой электромагнитной волне, и эти две волны отличаются ориентацией в пространстве векторов поля – поляризацией волн. Поэтому нам достаточно проанализировать только одну пару уравнений – например, (22.21).
по оси Oz, которое, в свою очередь, может создать электрическое поле только вдоль оси Оу. Составляющие полей из уравнений (22.22) при этом возникнуть не могут. Аналогиччная ситуация имеет место и для уравнений (22.22). Забегая вперед, отметим, что указанная особенность соотношений (22.21) и (22.22) отражает тот факт, что каждая из пар соответствует независимой электромагнитной волне, и эти две волны отличаются ориентацией в пространстве векторов поля – поляризацией волн. Поэтому нам достаточно проанализировать только одну пару уравнений – например, (22.21).
Продифференцируем первое уравнение в (22.20) по координате х и в правой части поменяем порядок дифференцирования и подставим значение  из второго уравнения:
из второго уравнения:
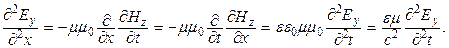 (22.23)
(22.23)
Такие же преобразования, но проведенные начиная со второго уравнения (22.21) приводят к уравнению для магнитной составляющей:
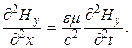 (22.24)
(22.24)
(22.23) и (22.24) являются частными случаями волновых уравнений (22.9) (22.10).
Простейшими решениями уравнений (22.23) и (22.24) (это можно проверить непосредственной подстановкой) являются функции:
 , (22.25)
, (22.25)
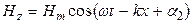 . (22.26)
. (22.26)
Подставив эти решения в волновые уравнения (22.23) и (22.24), придем к соотношениям:
 , (22.27)
, (22.27)
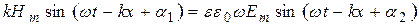 . (22.28)
. (22.28)
Для выполнения этих соотношений необходимо, чтобы совпадали амплитуды и фазы колебаний, записанных в левых и правых частях. Поэтому следует положить
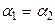 . (22.29)
. (22.29)
Таким образом, колебания электрической и магнитной составляющих в электромагнитной волне происходят синфазно.
Перемножив коэффициенты при синусах в (22.27), (22.28), получим соотношение:
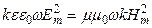 ,
,
определяющее связь амплитуд электрической и магнитной составляющих в электромагнитной волне:.
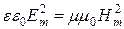 , (22.30)
, (22.30)
Положим теперь, что  , а
, а 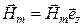 , и запишем уравнения плоской электромагнитной волны в виде:
, и запишем уравнения плоской электромагнитной волны в виде:
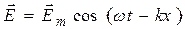 , (22.31)
, (22.31)
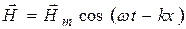 . (22.32)
. (22.32)
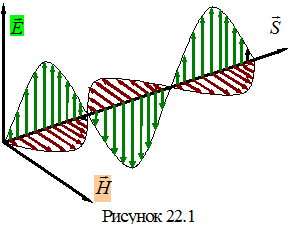
На рисунке показано взаимное расположение векторов плоской волны, удовлетворяющее всем полученным соотношениям.
22.3 Экспериментальное исследование электромагнитных волн в экспериментах Герца -№106.
Дата добавления: 2016-02-11; просмотров: 1670;
