Токи и напряжения в трехпортовой цепи

ПАРАМЕТРЫ РАССЕЯНИЯ

Классические матричные описания линейных многополюсников

Линейный многополюсник

Концепция 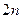- полюсников хорошо известна [10.1, 10.2] и изложена в любом стандартном учебнике по радиотехническим цепям или радиотехнике. Этот подход позволяет абстрагироваться от конкретной схемы и внутреннего устройства цепи и использовать некие общие параметры 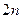-полюсника, связь между которыми и есть искомые характеристики.

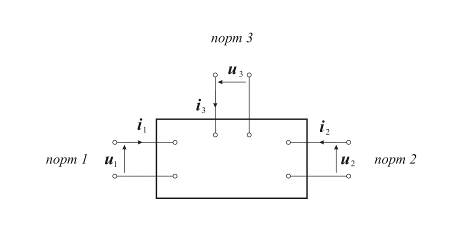
Токи и напряжения в трехпортовой цепи

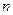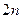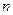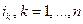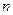Многополюсники ( -портовые цепи) разделяются на линейные и нелинейные. Далее рассматриваются только линейные многополюсники. Это понятие синонимично понятию линейная цепь. В традиционных представлениях многополюсников первичными параметрами возбужденного -полюсника являются выходных токов , и выходных напряжений ; ниже специально для диапазона СВЧ будет введена другая система первичных параметров. Пока нет необходимости конкретизировать вид математического описания токов и напряжений как первичных параметров (действительные величины, комплексные величины), их зависимость от времени и т. п.

Разбиение первичных параметров на группы А и В

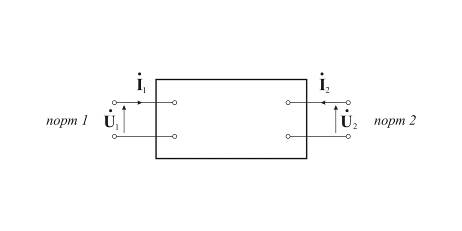
На рис. 10.1.1 показан 6-полюсник (3-портовая цепь) с произвольно выбранными положительными направлениями токов и напряжений. Разделим 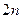первичных параметров на две группы по 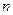параметров в каждой (необязательно, чтобы в одной группе были только токи, а в другой – только напряжения, а поэтому необязательно, чтобы параметры одной группы имели одинаковую размерность). Обозначим одну из групп буквой А, другую – буквой В.

Матричное соотношение групп параметров

В силу линейности многополюсника, первичные параметры связаны только линейными соотношениями друг с другом, а из законов Кирхгофа следует, что независимых из этих соотношений ровно 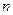. Удобно эти соотношения записать в виде выражений каждого параметра группы В со всеми параметрами группы А. Единственный линейный оператор в конечномерном 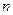-мерном пространстве – квадратная матрица порядка 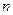. Поэтому систему искомых соотношений между первичными параметрами 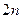-полюсника можно записать в виде:

,

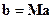(10.1.1)

где 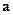= 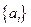– 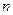-мерный вектор-столбец, составленный из параметров группы А;

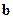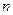= – -мерный вектор-столбец, составленный из параметров группы В;

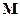
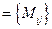– матрица 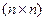с элементами необязательно одинаковой физической размерности.

Будем называть эту матрицу характеристической. Подчеркнем, что матрица 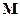получилась квадратной вследствие равенства числа 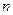параметров в каждой группе числу 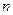независимых линейных соотношений между параметрами.

В расписанном виде равенство (10.1.1) имеет вид:

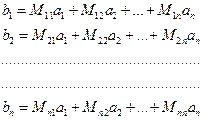
Уравнения этой системы называются основными уравнениями теории многополюсников. Коэффициенты системы основных уравнений, т. е. элементы 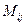, 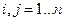матрицы 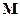составляют систему вторичных параметров многополюсника, описывающую его свойства в рамках концепции многополюсников.

В зависимости от разбиения первичных параметров на группы А и В, физический смысл (и размерности) систем вторичных параметров получаются разными, и в этом смысле системы вторичных параметров имеют разные представления. Всего, без учета перестановок элементов в группах, поскольку они не имеют принципиального значения, возможны

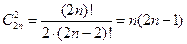
разбиения на группы А и В ( 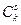– число сочетаний из 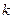по 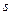, знак «!» обозначает факториал), столько же возможно разных по физическому смыслу систем вторичных параметров и соответствующих им характеристических матриц. Как видим, уже при 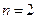(четырехполюсник) число таких матриц равно 6 (см. табл. 10.1.1 [10.1]), и с ростом 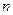быстро возрастает.

Система вторичных параметров многополюсника

Таблица 10.1.1

Четырехполюсник ( 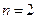). Варианты разбиения первичных параметров на группы А и В и матричного представления вторичных параметров

Варианты
Множ-во А
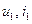
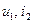
Множ-во В
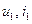
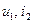
Обозн-ние мат-цы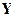

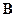
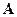
Однако на практике используются не все варианты характеристических матриц, а лишь те, что предоставляют некоторые удобства в тех или иных ситуациях. Понятно, что характеристические матрицы разных видов взаимно-однозначно связаны друг с другом.

Наиболее популярные классические системы параметров (z, y, a, h)