Лінійні вирішальні правила

За цим методом роздільна гіперповерхня задається у вигляді лінійної функції

,

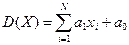де 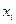– 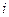-та ознака розпізнавання.

Лінійні вирішальні правила застосовуються у випадку лінійно поділених векторів реалізацій образу. Нехай, для випадку двох класів ( 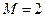) розподіл їх векторів-реалізацій показано на рис. 2.3.1.

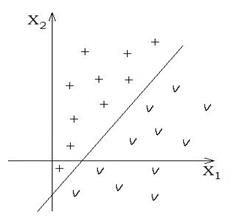
Рисунок 2.3.1.

У цьому випадку, алгоритм розпізнавання буде дуже простим:

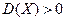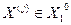IF THEN ELSE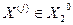

Якщо 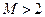, то функція роздільної гіперповерхні буде у вигляді не однієї лінійної функції, а у вигляді кусочно-лінійної функції.

Одним із прикладів реалізації лінійних вирішальних правил є перцептрон Розенблата (рис.2.3.2). Тут 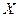– блоки множення, ПЕ – пороговий елемент.

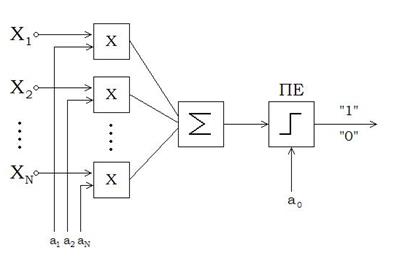
Рисунок 2.3.2

Задача навчання штучної нейромережі зводиться до цілеспрямованого підбору вагових коефіцієнтів з тим, щоб на виході перцептрона отримати мінімальну помилку

,

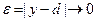де 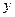– вихід штучної нейромережі; 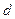– директивний сигнал (вказівка “учителя”).

Сигнал 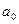безпосередньо впливає на поріг спрацьовування порогового елементу (рис.2.3.3).

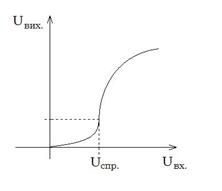
Рисунок 2.3.3

Лінійні вирішальні правила можуть застосовуватися для нормальних образів, тобто для класів розпізнавання, що не перетинаються. Якщо класи перетинаються, для них навчальна вибірка не є нормально розподіленою, а вектори- реалізації образів не є лінійно поділеними.