Метод еталонів, що дробляться

Цей метод спрямований на усунення модельності метода еталонів шляхом наближення до практичних задач, для яких є характерним перетин класів.

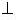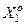На рисунку 2.2.1. зображено класи, які перетинаються. Тут , – графічне зображення реалізацій класів і 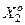відповідно.

Рисунок 2.2.1

Якщо гіперсфери перетинаються і в області перетину знаходяться реалізації більше ніж одного класу, то для них будуються контейнери другого рівня, потім третього, і т. д. До тих пір, поки контейнери не будуть перетинатися або в області перетину залишаться реалізації одного класу.

Переваги :

- метод враховує реальні апріорні розбиття класів розпізнавання, тобто що вони перетинаються;

- метод є відносно простий.

Недоліки :

- контейнери різних рівнів не є оптимальними в інформаційному розумінні;

- оскільки реалізації на практиці є випадковими, то фактична достовірність розпізнавання на екзамені може суттєво відрізнятися від асимптотичної достовірності, одержаної на етапі навчання, тобто цей метод не характеризується високою достовірністю розпізнавання.