Основні підходи до розв’язання задач розпізнавання образів

Підхід визначається галуззю знань і науковим напрямком вирішення проблем. У теперішній час основними підходами до вирішення проблем ТРО є:

1. Алгебраїчний.

Основна перевага: прості вирішальні правила.

Основний недолік: низька достовірність розпізнавання, оскільки не враховуються додаткові неконтрольовані фактори, які впливають на процес розпізнавання.

2. Геометричний. Він є універсальним підходом до вирішення проблем розпізнавання образів.

3. Статистичний, в рамках якого використовуються статистичні вирішальні правила (наприклад, Байєсівський класифікатор та його модифікації).

4. Біологічний (штучні нейронні мережі).Алгоритми реалізуються за аналогіями процесів, що відбуваються у нервових клітинах мозку людини.

Основний недолік: висока чутливість до багатовимірності простору ознак розпізнавання.

5. Мережний (семантичні мережі, фрейми, мережі Петрі, дерево рішень та інше).

Переваги: простота моделі, можливість її розширення та ускладнення.

Основний недолік: складність побудови вирішальних правил.

6. Нечіткий. Цей підход створений на базі алгебраїчного і є конкурентом статистичного підходу. Дозволяє моделювати складні слабоформалізовані процеси, де апріорне розбиття класів є нечітким. Але він не пристосований до оптимізації параметрів функціонування системи розпізнавання.

7. Теоретико-ігровий підхід, вирішальні правила у рамках якого характеризуються високою складністю та невисокою достовірністю розпізнавання.

Незважаючи на те, що наведені підходи відрізняються один від одного рівнем і видом математичної формалізації слабо формалізованих процесів прийняття рішень, між ними не існує чіткої межі, а самі підходи часто доповнюють один одного. Оскільки всі основні підходи, окрім алгебраїчного, перетинаються з геометричним, то саме в рамках геометричного підходу формування загальної теорії прийняття рішень є найбільш виправданим.

Розділ 2. Детерміновані методи ТРО

Основним критерієм визначення детермінованості методу розпізнавання образів є наявність детермінованих вирішальних правил.

У топологічному аспекті (у рамках геометричного підходу) такі вирішальні правила задаються геометричними параметрами контейнерів класів розпізнавання. Тобто, в режимі екзамену за детермінованими вирішальними правилами визначається належність вектора-реалізації образу що розпізнається одному із контейнерів класів розпізнавання із заданого алфавіта.

Метод еталонів

Суть метода: для кожного класу розпізнавання за навчальною матрицею будується еталонний вектор-реалізація, координатами якого є значення ознак розпізнавання. Для алфавіта класів 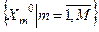еталонний вектор-реалізація має вигляд

,

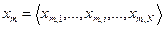де

.

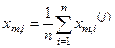Таким чином, еталонний вектор 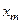є математичним сподіванням векторів-реалізацій класу 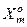. Він є абстрактним (фіктивним) вектором-реалізацією, який може не збігатися з будь-якою реалізацією образу.

Алгоритм розпізнавання подамо у вигляді предикатного виразу

,

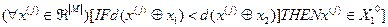де М=2; 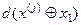, 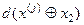- кодові відстані реалізацій, що виміряються від еталонного вектора першого класу 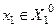та другого класу 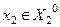відповідно.

Таким чином, прийняття рішень про належність реалізації відповідному класу здійснюються за дистанційним критерієм відстані реалізації відеталонних векторів відповідних класів.

Перевага: простота вирішального правила.

Основний недолік: метод носить модельний характер, оскільки виключає перетин класів розпізнавання.