Методи дослідження кінематики плоских механізмів з вищими кінематичними парами. Основна теорема плоского зачеплення. Спряжені профілі

Найбільш часто в задачах дослідження кінематики плоских механізмів з вищими кінематичними парами, в яких передача обертального руху здійснюється між ланками з паралельними осями, використовується метод центроїд.

Нерухома центроїда – геометричне місце миттєвих центрів обертання плоскої фігури, що рухається, в нерухомій площині. Рухома центроїда – геометричне місце миттєвих центрів швидкостей в площині, пов’язаній з рухом плоскої фігури. При русі плоскої фігури в її площині рухома центроїда котиться без ковзання по нерухомій, тобто довжини відповідних дуг рухомої і нерухомої центроїд рівні. Зворотна теорема про центроїди – всякий рух плоскої фігури в її площині можна здійснити шляхом обкочування без ковзання рухомої центроїди по нерухомій з відповідною в даний момент кутовою швидкістю.

Миттєвий центр швидкостей Рє точкою плоскої фігури, швидкість якої в даний момент дорівнює 0 (визначається як точка перетину перпендикулярів, встановлених з будь-яких двох точок фігури до векторів швидкостей цих точок). В кожний момент часу з ним співпадає миттєвий центр обертання– точка нерухомої площини, повертанням навколо якої плоска фігура переміщується з даного положення в положення, нескінченно близьке до даного.

В механізмі, кінематична схема якого представлена на рисунку 1.6, ланки 1 і 2, що обертаються відносно осей А і С, утворюють вищу кінематичну пару В в точці контакту (K₁,K₂ – елементи ланок 1 і 2 відповідно).

Знайдемо центроїди як геометричні місця миттєвих центрів обертання і швидкостей. Використовуючи метод обернення руху (ланкам 1 і 2 додатково надається кутова швидкість «-ω₁» після чого ланка 1 розглядається як нерухома), можна вказати напрямок відносних швидкостей точок С і K₂ відносно точок нерухомої ланки 1 – швидкості 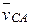точки С відносно осі А, вектор якої перпендикулярний міжосьовій відстані АС і швидкості ковзання 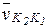точки K₂, вектор якої спрямований вздовж загальної дотичної t – t до профілів, що контактують в точці В. Тоді миттєвий центр швидкостей Р ланки 2 і співпадаючий з ним миттєвий центр обертання у відносному русі знаходяться у точці перетину міжосьової відстані АС і загальної нормаліn – n ( 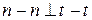) до профілів, встановленої в загальній контактній точці С. 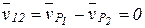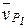Швидкість відносного руху в точці Р дорівнює 0 - , де і 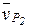- вектори швидкості точок Р₁ і Р₂ при обертанні їх навколо відповідно осей А і С. Тоді справедливим буде рівняння 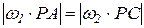, з якого можна виразити передаточне відношення

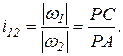(1.2)

Миттєвий центр швидкостей Р називають полюсом зачеплення (термін «зачеплення» в даному випадку є синонімом терміну «вища КП»). В дослідженнях зубчатого зачеплення центри обертання ланок 1 і 2 найчастіше позначаються літерою О з індексами 1 і 2 – О₁ і О₂ (замість А і С на рисунку 1.6). При таких позначеннях формула (1.2) набуває вид

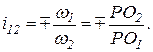(1.3)

Таким чином полюс зачеплення Р ланок 1 і 2 (рисунок 1.6) у відносному русі лежить на міжосьовій лінії О₁О₂ (АС) і ділить міжосьову відстань на відрізки РО₁ (АР) і РО₂ (РС), відношення довжин яких обернено пропорційно відношенню миттєвих кутових швидкостей ланок (у тому числі і зубчатих коліс).

Позначимо міжосьову відстань О₁О₂ через a_w, а відстані РО₁ і РО₂ (радіуси центроїд) - 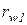і 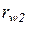відповідно. При таких позначеннях

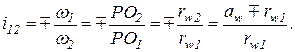(1.4)

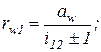
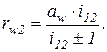(1.5)

З формул (1.5) видно, що при сталому передаточному відношенні радіуси центроїд 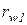і 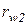також сталі. Отже, при передачі обертального руху між ланками з паралельними осями обертання при 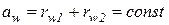і 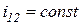центроїди є окружностями. В теорії зубчатих зачеплень центроїди називаються початковими колами.

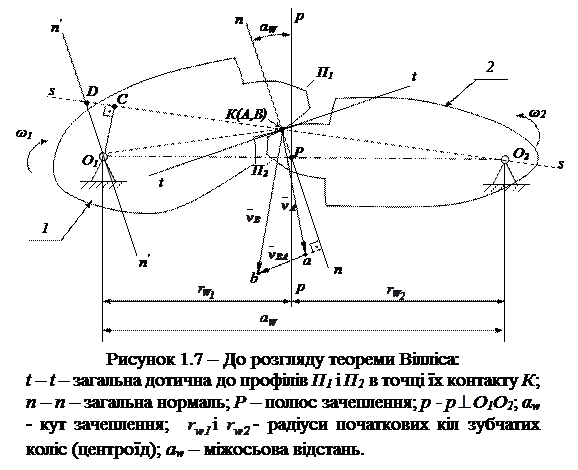
Основна теорема плоского зачеплення (теорема Вілліса – Willis R. Principles of mechanism. London, 1841). Загальна нормаль в точці контакту спряжених профілів в будь-який момент зачеплення повинна проходити через полюс зачеплення Р, положення якого на міжосьовій лінії визначається заданим відносним рухом ланок О₁О₂.

З рівняння (1.5) видно, що положення полюса Р однозначно визначається через радіус 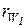, якщо задані міжосьова відстань 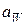і передаточне відношення 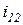. Для доказу теореми Вілліса в точці контакту К профілів зубців П₁ і П₂ зубчатих коліс 1, 2 (рисунок 1.7) розглядаються вектори швидкості точок А і В (належать відповідно ланкам 1 і 2 і співпадають з точкою К) і співвідношення між ними - .

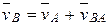Напрямки векторів визначають з умов руху точок: 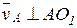; ; 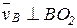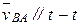або 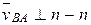. Через вісь О₁ проводиться лінія 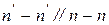, яка перетинається в точці D з лінією 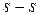, що проходить через вісь О₂, точку контакту К і точку С. Отриманий 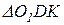подібний 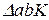, який утворено векторами .

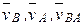З подібності трикутників витікає

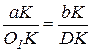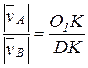, або , або .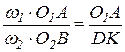

З формули 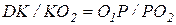, яка витікає з умови перетинання сторін кута DO₁O₂ двома паралельними прямими, можна записати співвідношення

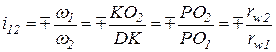. (1.6)

Співвідношення (1.4) і (1.6) ідентичні, що є доказом проходження загальної нормалі n – n через полюс зачеплення Р.

Довжина початкового кола і - го зубчатого колеса в ЗП, що має число зубців 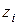, через початковий крок 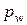(відстань між однойменними профілями двох сусідніх зубців за дугою початкового кола) визначається як 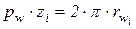. Звідкіля 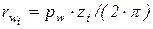. Якщо підставити даний вираз в формулу (1.6), то отримується залежність передаточного відношення ЗП від числа зубців зубчатих коліс

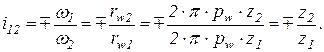(1.7)

Згідно ГОСТ 16530-83 модуль відношення чисел зубців відповідає передаточному числу ЗП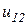

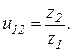(1.8)

З теореми Вілліса витікає, що для забезпечення сталого передаточного відношення ( 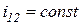) в ЗП, спряжені профілі повинні розташовуватися відносно центроїд так, щоб в будь-якій точці контакту загальна нормаль n – n проходила через незмінно розташований на міжосьові лінії O₁O₂ полюс зачеплення Р.