Случай задержки распространения длительностей импульса

ОСНОВНЫЕ ФУНКЦИИ ПРОЦЕССОРОВ.

Вычислительные машины являются техническими средствами, предназначенными для автоматического преобразования информации. При этом существо процесс преобразования информации задается в виде алгоритма.

Работа ЭВМ заключается в следующем. По сигналу устройства управления из памяти команд извлекается команда. Выбранная команда поступает в устройство управления и расшифровывается. По результатам расшифровки команды вырабатываются необходимые управляющие сигналы, которые поступая в устройства ввода, вывода и памяти, обеспечивают подачу необходимых операндов в арифметическое устройство. Далее в арифметическом устройстве под действием очередных управляющих сигналов производится заданная операция. Результат операции направляется в память данных по соответствующему адресу, а в устройство управления передается очередная команда и описанный цикл повторяется.

Роль процессора в структуре ЭВМ определяется его функциями, основные функции процессора могут быть заданы следующими пятью операциями:

1. Произвести считывание входного символа «x».

2. Сравнить «x» с «z» - внутренним состоянием процессора.

3. Вывести соответствующий символ «у».

4. Изменить внутреннее состояние «z» на новое состояние «x».

5. Повторить описанную последовательность действий для нового входного
символа «x».

МАШИНА ПОСТА - ВАРИАНТ МИНИМАЛЬНОГО ПРОЦЕССОРА.

На рубеже З0х - 40х годов 20-го столетия американский математик Эмиль Л. Пост предложил гипотетическую систему обработки информации. Так называемую «машину Поста». Алгоритмическая система Поста наиболее близка к структуре ЭВМ.

Данная система может выполнять некоторый набор операций, обеспечивающий преобразования информации, представленной в двоичном алфавите.

Рассмотрим структуру машины Поста.

В этой машине входная, выходная и промежуточная информация размещается в памяти бесконечного объема. Память представляет собой массив, состоящий из последовательно расположенных ячеек. В каждую ячейку может быть записана одна двоичная цифра - бит. Ячейка считается отмеченной, если в ней записана 1, и не отмеченной если в ячейке содержится 0.

Преобразование информации в машине Поста происходит по шагам. В течение каждого шага выполняется одна команда, и машина взаимодействует с какой-либо одной ячейкой памяти. Ячейка, с которой на данном шаге взаимодействует машина, называется активной.

Машина Поста выполняет операции пяти типов:

1. Отметить активную ячейку памяти (т.е. записать в нее 1).

2. Записать в активную ячейку 0.

3. Выбрать в качестве активной следующую по порядку левую ячейку.

4. Выбрать в качестве активной следующую по порядку правую ячейку.

5. Определить, отмечены или нет активная ячейка.

Команды машины Поста могут быть следующих видов:

- совершить операцию одного из первых четырех типов и затем перейти к
выполнению і-й команды;

- совершить операцию пятого типа и, если ответ будет «да», перейти к
выполнению j-й команды, а если «нет», то і-й команды;

- останов.

Алгоритмы составляемые из любого конечного числа описанных команд, называют алгоритмами Поста. В теории алгоритмов доказано, что класс алгоритмов Поста совпадает с классом всех нормализуемых алгоритмов. Это приводим к следующему утверждению:

Если операции реально существующей вычислительной машины могут быть приведены или с их помощью можно реализовать команды машины Поста, то на такой вычислительной машине можно реализовать любые процессы преобразования информации.

Необходимо отметить, что возможность технической реализации абсолютно любых процессов обработки информации ограничено принципиальной невозможностью создания памяти бесконечного объема.

Однако это ограничение сглаживается тем, что практически всегда можно расширить объем памяти до требуемого (но все же конечного) или вводить входную информацию и даже программу в ЭВМ по частям, рассмотрим обобщенную структурную схему ЭВМ.

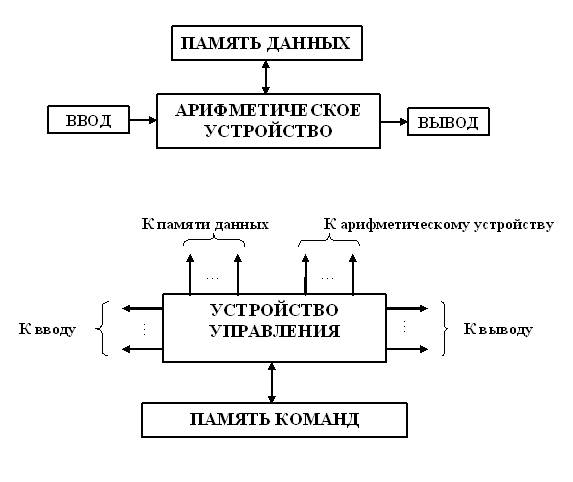
Данная структура соответствует возможной структуре машины Поста. Для полного соответствия следует считать, что устройства ввода и вывода информации для арифметического устройства и устройства управления адекватны ячейкам памяти данных.

Таким образом, машину Поста можно рассматривать как минимальную ЭВМ, или, если не рассматривать устройства памяти, как минимальный процессор.

Для работы процессора необходимо наличие исходной (преобразуемой) информации и информации о процессе преобразования.

Взаимосвязь аппаратных средств и программного обеспечения первоначально основывалась на соображениях экономического характера. В этой связи определяющим было правило: аппаратные средства обеспечивают быстродействие, программное обеспечение - дешевизну, вследствие чего доминировали простые, преимущественно программные системы с невысоким быстродействием. В процессе развития данные соображения претерпели изменения. Быстрыми темпами идет наращивание вычислительной мощности аппаратных средств, при этом стоимость их неуклонно снижается.

Существует утверждение, основанное на опыте и принимаемое как аксиома:

Любой процесс, реализуемый программным путем, может быть преобразован в эквивалентный процесс, реализуемый аппаратными средствами, и наоборот.

Ни аппаратные средства, ни программное обеспечение не существуют независимо, поэтому указанное преобразование никогда не может быть завершено полностью, всегда должны существовать программы управления аппаратными средствами и аппаратура, при помощи которой реализуются программные алгоритмы.

Изменения алгоритма по-разному сказывается на аппаратуре и программном обеспечении. Обычно программная реализация алгоритма позволяет вносить значительные изменения, в то время как возможность изменения существующего аппаратного предоставления алгоритма практически отсутствует. Зачастую разнится и способ выполнения алгоритма при этих подходах: обработка посредством аппаратных средств является непрерывным параллельным одношаговым процессом, программная же обработка, как правило, состоит из ряда дискретных последовательных шагов, например умножение двух двоичных чисел. Эта операция аппаратно может быть выполнена за один шаг без каких - либо промежуточных результатов, в то время как программная реализация алгоритма умножения с использованием аппаратно выполненных сумматоров распадается на несколько отдельных шагов, на каждом из которых получается промежуточный результат.

Основные постулаты алгебры логики.

1. Если подмножества А и В принадлежат множеству U, то и
подмножество А и В (А · В) принадлежит этому множеству U.

2. Если подмножества А и В принадлежат множеству U, то и подмножество
А или В (А + В) принадлежит этому множеству U.

3. Для всякого элемента А множества U имеется элемент 0, такой что
А + 0 = А.

4. Для всякого элемента А множества U имеется элемент 1, такой что
А · 1 = А.

5. Если А, В, С - элементы множества U, то

а ) А + (В + С) = (В + А) + С = (А + С) + В и т.д.

б) (А · В) · С = А · (В · С) и т.д.

в) А + (В · С) = (А + В) · (А + С) - левое распределение относительно « +».

г) А · (В + С) = (А · В) + (А · С) - левое распределение относительно « ·».

6. Если 0 или 1 единственны, тогда для каждого элемента А множества U
найдется такой элемент Āэтого же множества, что А · Ā = 0 и А + Ā = 1.

7. А, В и C таковы, что A ≠ B ≠ C.

На этих постулатах базируется следующие теоремы.

Теоремы:

1. а) А + А = А; б) А · А = А

2. а) А + 1 = 1; б) А · 0 = 0

3. а) А + 0 =А; б) А · 1 = А

4. а) (Ā) = Ā ; б) (Ā) = А

5. а) А + Ā = 1; б) А · Ā = 0

6. а) А + В + С + ... = А · В · С ·...; б) А · В· С ·...= А + В + С +... (теорема де Моргана).

7. а) А · (А + В) = А + А · В = А; б) А + (А · В) = А · (А + В) = А

Теоремы «а» и «б» являются двойственными. Двойственность обусловлена возможностью взаимной замены всех И и ИЛИ, а также всех 1 и 0. Если Булево выражение истинно, то и двойственное ему выражение истинно.

Операции инвертирования, ИЛИ, И, ИЛИ-НЕ, И-НЕ и исключающее слово ИЛИ можно применять к двоичным числам.

Двоичное число в вычислительной машине не занимает ряд разрядов. Каждый разряд можно рассматривать как одну двоичную переменную. Так как логические операции можно выполнить с двумя двоичными числами, каждую пару разрядов можно рассматривать как две двоичные переменные. Запись действий с использованием терминов И, ИЛИ и дополнения НЕ называется сигнально - ориентированной. Кроме того, используется диаграмно-ориентированная запись - диаграммы Венна. В них используются соответственно понятия пересечения и объединения.

Например:

А = 101000110010

В = 011101011011

Ā = 010111001101

А Ā

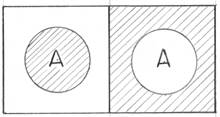
А · В = 001000010010

А + В = 111101111011

А·В (и) А+В (или)

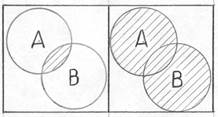
А · В = 110111101101

А + В = 000010000100

А·В (и-не) А+В (или-не)

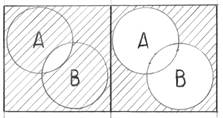
(А + В) · (А · В) = 110101101001

(А+В)·(А·В)

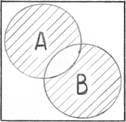
Исключающее ИЛИ

Например:

Доказать двумя различными способами, что А · (Ā + В) = А · В

Способ 1. Используем диаграмму Венна:

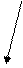А·В А·(Ā+В)

Способ 2. На основании постулатов:

А · (Ā + В) = А · Ā + А · В

А · Ā = 0, поэтому

А·(Ā + В) = А·В

СИНХРОНИЗАЦИЯ.

Таблицы истинности логических схем показывают установившееся состояние входных и выходных величин. Однако, когда в качестве входных сигналов используются электрические импульсы, то необходимо некоторое время для того, чтобы выходные величины достигли уровня установившегося состояния из-за внутренних задержек в схемах. Задержка одной схемы обычно мала, однако проходя через множество схем, задержка может стать значительной. В этом случае необходимо выделить отрезок времени (такт) на каждый шаг операции. Если операция завершается раньше, чем заканчивается тактовое время, машина ожидает его окончания. В результате скорость выполнения операции несколько снижается, но достигается высокая надежность т.к. обеспечена синхронизация между многими параллельно выполняющимися операциями. Синхронизация устройств ЭВМ обеспечивается с помощью специального генератора. В качестве такого генератора обычно служит генератор, работающий в автоколебательном режиме и формирующий импульсы стабильной частоты.

Синхроимпульсы

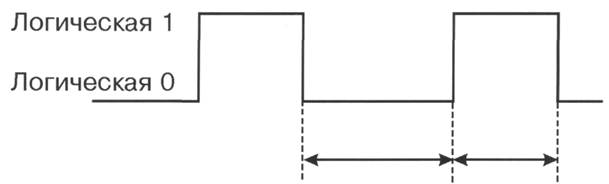
n – наиболее неблагоприятный Наибольшая из минимальных

случай задержки распространения длительностей импульса