Метод отклонений от тренда
Пусть имеются два временных ряда 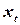 , и
, и 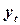 , каждый из которых содержит трендовую компоненту Т и случайную компоненту
, каждый из которых содержит трендовую компоненту Т и случайную компоненту 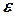 . Проведение аналитического выравнивания по каждому из этих рядов позволяет найти параметры соответствующих уравнений трендов и определить расчетные по тренду уровни
. Проведение аналитического выравнивания по каждому из этих рядов позволяет найти параметры соответствующих уравнений трендов и определить расчетные по тренду уровни 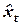 , и
, и 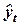 соответственно. Эти расчётные значения можно принять за оценку трендовой компоненты
соответственно. Эти расчётные значения можно принять за оценку трендовой компоненты 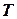 каждого ряда. Поэтому влияние трендовой компоненты можно устранить путём вычитания расчётных значений уровней ряда из фактических. Эту процедуру проделывают для каждого временного ряда в модели. Дальнейший анализ взаимосвязи проводят с использованием не исходных уровней, а отклонений от тренда
каждого ряда. Поэтому влияние трендовой компоненты можно устранить путём вычитания расчётных значений уровней ряда из фактических. Эту процедуру проделывают для каждого временного ряда в модели. Дальнейший анализ взаимосвязи проводят с использованием не исходных уровней, а отклонений от тренда 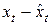 и
и 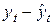 при условии, что последние не содержат тенденции.
при условии, что последние не содержат тенденции.
Пример. Рассмотрим данные предыдущих примеров и оценим их взаимосвязь методом отклонения от тренда. Для этого из аддитивного временного ряда удалим сезонные колебания по формуле 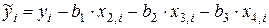 . А из мультипликативного ряда по формуле
. А из мультипликативного ряда по формуле 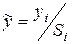 . Полученные значения запишем в виде таблицы.
. Полученные значения запишем в виде таблицы.
| № | 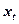 
| 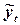
|
| 8,0875 | 78,86 | |
| 8,875 | 83,19 | |
| 8,9125 | 83,18 | |
| 79,7 | ||
| 9,2875 | 76,67 | |
| 9,275 | 76,54 | |
| 9,9125 | 73,94 | |
| 72,23 | ||
| 10,0875 | 67,91 | |
| 10,075 | 66,56 | |
| 10,3125 | 62,85 | |
| 59,78 | ||
| 11,0875 | 56,96 | |
| 11,075 | 49,92 | |
| 11,9125 | 46,21 | |
| 10,8 | 37,36 |
Проведём корреляционный анализ. Получим
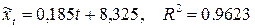 и и 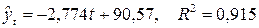 , ,
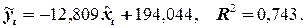
|
Можно предположить, что полученные результаты содержат ложную корреляцию ввиду наличия в каждом из рядов линейной или близко к линейной тенденции. Применим метод устранения тенденции по отклонениям от тренда.
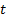
| 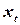
| 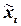
| 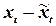
| 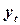
| 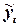
| 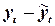
|
| 8,09 | 8,51 | -0,42 | 78,86 | 87,8031 | -8,9431 | |
| 8,88 | 8,70 | 0,18 | 83,19 | 85,0282 | -1,8382 | |
| 8,91 | 8,89 | 0,03 | 83,18 | 82,2533 | 0,9267 | |
| 9,00 | 9,08 | -0,07 | 79,7 | 79,4784 | 0,2216 | |
| 9,29 | 9,26 | 0,03 | 76,67 | 76,7035 | -0,0335 | |
| 9,28 | 9,45 | -0,18 | 76,54 | 73,9286 | 2,6114 | |
| 9,91 | 9,64 | 0,28 | 73,94 | 71,1537 | 2,7863 | |
| 10,00 | 9,83 | 0,18 | 72,23 | 68,3788 | 3,8512 | |
| 10,09 | 10,01 | 0,08 | 67,91 | 65,6039 | 2,3061 | |
| 10,08 | 10,20 | -0,13 | 66,56 | 62,829 | 3,731 | |
| 10,31 | 10,39 | -0,07 | 62,85 | 60,0541 | 2,7959 | |
| 11,00 | 10,58 | 0,43 | 59,78 | 57,2792 | 2,5008 | |
| 11,09 | 10,76 | 0,33 | 56,96 | 54,5043 | 2,4557 | |
| 11,08 | 10,95 | 0,13 | 49,92 | 51,7294 | -1,8094 | |
| 10,91 | 11,14 | -0,23 | 46,21 | 48,9545 | -2,7445 | |
| 10,80 | 11,33 | -0,52 | 37,36 | 46,1796 | -8,8196 |
Проверим полученные отклонения от трендов на автокорреляцию. Коэффициенты автокорреляции первого порядка по отклонениям от трендов составляют 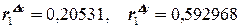 . Следовательно, временные ряды отклонений от трендов можно использовать для получения количественной характеристики тесноты связи исходных временных рядов. Проведём корреляционный анализ. Получим
. Следовательно, временные ряды отклонений от трендов можно использовать для получения количественной характеристики тесноты связи исходных временных рядов. Проведём корреляционный анализ. Получим 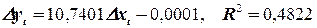 . Содержательная интерпретация параметров этой модели затруднительна, однако её можно использовать для прогнозирования.
. Содержательная интерпретация параметров этой модели затруднительна, однако её можно использовать для прогнозирования.
Дата добавления: 2016-02-09; просмотров: 1821;
