Эконометрика - лекции 4 страница
2) Составить уравнение регрессии в стандартизованном виде и в натуральном масштабе.
Найдём основные числовые характеристики, среднее квадратическое отклонение найдём как корень из дисперсии, которая находится через Excel используя функцию «Дисп»
| Среднее значение | 61,776 | 15,80467 | 9,5844 | 20,0672 | 26,15667 |
Среднее квадратическое
oтклонение 
| 17,60612 | 8,198498 | 11,31237 | 10,37851 | 13,86945 |
Составим матрицу парных коэффициентов корреляции используя Excel «анализ данных», «корреляции»

| 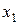
| 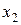
| 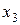
| 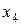
| |

| 0,742113 | 0,469343 | -0,30962 | 0,782799 | |
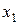
| 0,742113 | 0,117338 | -0,03446 | 0,643305 | |
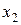
| 0,469343 | 0,117338 | 0,176933 | 0,833674 | |
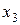
| -0,30962 | -0,03446 | 0,176933 | 0,113465 | |
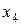
| 0,782799 | 0,643305 | 0,833674 | 0,113465 |
1. Проверим факторы на мультиколлинеарность. Для вычислим расчётное значение 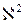 по формуле
по формуле  , где:
, где: 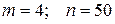 ;
; 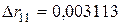 подставив значения, получим 46,86917. Используя Excel и функцию ХИ2ОБР(0,05;6) где 6 число степеней свободы находим критическое значение равное 12,59159 . Следовательно, в данном наборе факторов присутствует мультиколлинеарность. Определим фактор ответственный за мультиколлинеарность. Анализ матрицы парных коэффициентов позволяет предположить, что это
подставив значения, получим 46,86917. Используя Excel и функцию ХИ2ОБР(0,05;6) где 6 число степеней свободы находим критическое значение равное 12,59159 . Следовательно, в данном наборе факторов присутствует мультиколлинеарность. Определим фактор ответственный за мультиколлинеарность. Анализ матрицы парных коэффициентов позволяет предположить, что это 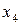 , так он имеет большие коэффициенты корреляции с остальными факторами. Проверим, это используя значения определителя межфакторной корреляции при удалении одного фактора. Если удалить
, так он имеет большие коэффициенты корреляции с остальными факторами. Проверим, это используя значения определителя межфакторной корреляции при удалении одного фактора. Если удалить 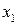 получим значение
получим значение 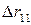 равное 0,294281, при удалении
равное 0,294281, при удалении 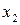 получим 0,567066, при удалении
получим 0,567066, при удалении  получим 0,003236, при удалении
получим 0,003236, при удалении 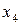 получим 0,952308. Следовательно, удаляя
получим 0,952308. Следовательно, удаляя 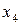 , мы получаем наибольшее значение определителя межфакторной корреляции. Проверим на мультиколлинеарность оставшиеся три фактора. Найдём расчётное значение критерия
, мы получаем наибольшее значение определителя межфакторной корреляции. Проверим на мультиколлинеарность оставшиеся три фактора. Найдём расчётное значение критерия 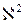 равное 2,371397, критическое значение критерия при степенях свободы равном 3 составляет 7,814728. Следовательно, при удалении четвертого фактора мы избавляемся от мультиколлинеарности. Этот же вывод можно сделать проанализировав матрицу парных коэффициентов корреляции. Очевидно, что факторы
равное 2,371397, критическое значение критерия при степенях свободы равном 3 составляет 7,814728. Следовательно, при удалении четвертого фактора мы избавляемся от мультиколлинеарности. Этот же вывод можно сделать проанализировав матрицу парных коэффициентов корреляции. Очевидно, что факторы 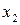 и
и 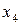 находятся в линейной зависимости и поэтому нужно удалить один из них. Но как указано ранее
находятся в линейной зависимости и поэтому нужно удалить один из них. Но как указано ранее 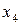 имеет большие коэффициенты корреляции с остальными факторами. Поэтому удаляем
имеет большие коэффициенты корреляции с остальными факторами. Поэтому удаляем 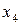 а оставляем
а оставляем 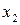 . Правда при этом может возникнуть ситуация когда один удаляемый фактор оказывает большее влияние на результативный признак чем три оставшихся. В этом случае оставляют самый значимый признак и к нему присоединяют по одному оставшиеся факторы, на каждом шаге проверяя наличие мультиколинеарности.
. Правда при этом может возникнуть ситуация когда один удаляемый фактор оказывает большее влияние на результативный признак чем три оставшихся. В этом случае оставляют самый значимый признак и к нему присоединяют по одному оставшиеся факторы, на каждом шаге проверяя наличие мультиколинеарности.
2. Составим уравнение регрессии в стандартизованном масштабе. Для этого составим систему уравнений 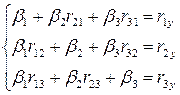 тогда
тогда 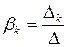 или
или 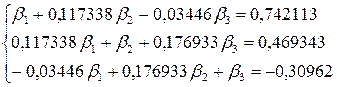
решаем полученную систему методом Крамера, используя Excel и функцию «МОПРЕД» вычисляем требуемые определители и найдём значения, коэффициенты 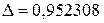 ,
, 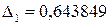 ,
, 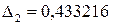 ,
, 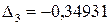 получаем уравнение в стандартизованном масштабе
получаем уравнение в стандартизованном масштабе  . Найдем уравнение в натуральном масштабе. Для этого найдём коэффициенты регрессии используя формулу
. Найдем уравнение в натуральном масштабе. Для этого найдём коэффициенты регрессии используя формулу 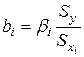 и параметр регрессии по формуле
и параметр регрессии по формуле 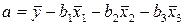 получаем
получаем 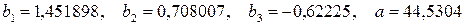 . Следовательно, уравнение регрессии в натуральном масштабе имеет вид:
. Следовательно, уравнение регрессии в натуральном масштабе имеет вид: 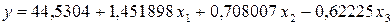 .
.
Множественная корреляция
Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком, или оценивает тесноту совместного влияния факторов на результат. Независимо от формы связи показатель множественной корреляции может быть найден по формуле 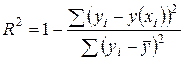 . Величина показателя множественной корреляции больше или равна максимальному парному индексу корреляции. При линейной зависимости признаков формула показателя корреляции равна
. Величина показателя множественной корреляции больше или равна максимальному парному индексу корреляции. При линейной зависимости признаков формула показателя корреляции равна  , где:
, где: 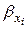 - стандартизованные коэффициенты регрессии;
- стандартизованные коэффициенты регрессии; 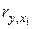 - парные коэффициенты корреляции результативного признака с каждым фактором. Также при линейной зависимости можно определить показателя корреляции по формуле
- парные коэффициенты корреляции результативного признака с каждым фактором. Также при линейной зависимости можно определить показателя корреляции по формуле  , где:
, где: 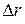 - определитель матрицы парных коэффициентов корреляции;
- определитель матрицы парных коэффициентов корреляции;  - определитель матрицы межфакторной корреляции. Проверка значимости уравнения регрессии в целом проводится с использованием
- определитель матрицы межфакторной корреляции. Проверка значимости уравнения регрессии в целом проводится с использованием 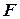 - критерия Фишера. Для этого находится расчетное значение критерия по формулам
- критерия Фишера. Для этого находится расчетное значение критерия по формулам  или
или 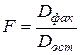 которое затем сравнивается с критическим при уровне значимости
которое затем сравнивается с критическим при уровне значимости 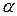 и степенях свободы большей дисперсии
и степенях свободы большей дисперсии 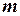 и меньшей дисперсии
и меньшей дисперсии  . Если наблюдаемое значение меньше критического то нулевая гипотеза о не значимости уравнения регрессии принимается, в противном случае уравнение регрессии значимо. Расчетные значения показателя множественной корреляции, полученные по разным формулам должны совпадать. Так же как расчетные значения критерия Фишера. Средняя ошибка аппроксимации находится так же как и при парной регрессии.
. Если наблюдаемое значение меньше критического то нулевая гипотеза о не значимости уравнения регрессии принимается, в противном случае уравнение регрессии значимо. Расчетные значения показателя множественной корреляции, полученные по разным формулам должны совпадать. Так же как расчетные значения критерия Фишера. Средняя ошибка аппроксимации находится так же как и при парной регрессии.
Продолжение примера.
3) Найдите индекс множественной корреляции тремя способами и сравните полученные значения.
4) Оценить значимость уравнения регрессии по критерию 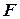 значение критерия рассчитать двумя способами, оцените качество уравнения через среднюю ошибку аппроксимации.
значение критерия рассчитать двумя способами, оцените качество уравнения через среднюю ошибку аппроксимации.
Решение: Составим расчётную таблицу
| 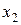
| 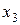
| 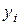
| 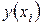
| 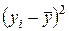
| 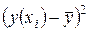
| 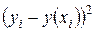
| 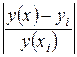
|
| 24,00 | 5,30 | 24,56 | 59,69 | 67,84593 | 4,351396 | 36,84404 | 66,51918 | 0,136638 |
| 6,75 | 16,08 | 28,01 | 53,71 | 48,28624 | 65,06036 | 181,9736 | 29,41716 | 0,100982 |
| 19,32 | 17,06 | 22,46 | 81,44 | 70,67909 | 386,6729 | 79,26508 | 115,7971 | 0,132133 |
| 19,60 | 0,76 | 10,79 | 74,58 | 66,81161 | 163,9424 | 25,35735 | 60,3479 | 0,104162 |
| 2,47 | -9,96 | 5,90 | 36,29 | 37,38872 | 649,5362 | 594,7392 | 1,207194 | 0,030276 |
| 24,67 | 17,96 | 13,40 | 95,185 | 84,72154 | 1116,161 | 526,4978 | 109,484 | 0,109928 |
| 28,13 | 4,80 | -3,10 | 82,955 | 90,70454 | 448,55 | 836,8604 | 60,05535 | 0,093419 |
| 14,83 | 15,58 | 17,87 | 58,24 | 65,97803 | 12,5033 | 17,65704 | 59,87709 | 0,132865 |
| 27,57 | 37,52 | 25,70 | 82,735 | 95,12699 | 439,2797 | 1112,288 | 153,5613 | 0,149779 |
| 11,88 | 28,08 | 21,20 | 58,125 | 68,47292 | 13,3298 | 44,8488 | 107,0795 | 0,178029 |
| 20,48 | 30,56 | 35,09 | 62,21 | 74,07205 | 0,188356 | 151,1929 | 140,7083 | 0,190678 |
| 7,90 | 10,36 | 31,07 | 47,335 | 44,00204 | 208,5425 | 315,9137 | 11,10863 | 0,070412 |
| 18,15 | 14,26 | 8,87 | 89,795 | 75,45917 | 785,0644 | 187,2292 | 205,516 | 0,159651 |
| 29,40 | 29,08 | 21,08 | 85,29 | 94,68801 | 552,9082 | 1083,201 | 88,32268 | 0,110189 |
| -6,85 | 2,06 | 31,61 | 14,775 | 16,37407 | 2209,094 | 2061,335 | 2,557027 | 0,108228 |
| 18,25 | 0,66 | 19,31 | 65,04 | 59,47918 | 10,6537 | 5,275402 | 30,92277 | 0,085499 |
| 11,40 | 2,16 | 18,62 | 45,04 | 51,02504 | 280,0937 | 115,5832 | 35,82067 | 0,132883 |
| 12,93 | 20,74 | 16,19 | 69,31 | 67,91812 | 56,76116 | 37,72562 | 1,937334 | 0,020082 |
| 9,62 | 10,14 | 13,28 | 58,71 | 57,40853 | 9,400356 | 19,07479 | 1,693824 | 0,022168 |
| 17,95 | 16,00 | 15,08 | 85,915 | 72,53655 | 582,6913 | 115,7895 | 178,9829 | 0,155717 |
| 17,88 | 8,30 | 33,26 | 60,605 | 55,6756 | 1,371241 | 37,21489 | 24,29899 | 0,081337 |
| 22,25 | -0,28 | 30,41 | 60,605 | 57,71427 | 1,371241 | 16,49768 | 8,356343 | 0,047698 |
| 24,43 | -0,22 | 31,43 | 57,795 | 60,29203 | 15,84836 | 2,202171 | 6,235153 | 0,043205 |
| 18,62 | -0,92 | 18,71 | 64,325 | 59,26624 | 6,497401 | 6,29891 | 25,59108 | 0,078644 |
| -4,52 | 5,22 | 31,37 | 22,895 | 22,14847 | 1511,732 | 1570,341 | 0,5573 | 0,032606 |
| -2,32 | 12,54 | 2,39 | 50,805 | 48,55807 | 120,3628 | 174,7138 | 5,04871 | 0,044227 |
| 17,97 | -0,56 | 17,93 | 59,155 | 59,06274 | 6,869641 | 7,361775 | 0,008512 | 0,00156 |
| 23,35 | 3,26 | 25,46 | 59,47 | 64,89784 | 5,317636 | 9,745861 | 29,4614 | 0,09127 |
| 10,50 | 8,10 | 20,33 | 56,215 | 52,85984 | 30,92472 | 79,49785 | 11,25708 | 0,059684 |
| 23,00 | 18,30 | 34,94 | 68,92 | 69,13917 | 51,03674 | 54,21623 | 0,048034 | 0,00318 |
| 12,93 | 7,62 | 23,99 | 49,62 | 53,77552 | 147,7683 | 64,00773 | 17,26832 | 0,083747 |
| 9,88 | 14,36 | 23,81 | 51,415 | 54,2312 | 107,3503 | 56,92401 | 7,930982 | 0,054774 |
| 8,02 | 5,10 | -1,69 | 54,19 | 60,83222 | 57,5474 | 0,89072 | 44,11909 | 0,122573 |
| 16,97 | 9,40 | 11,99 | 55,395 | 68,35876 | 40,71716 | 43,3327 | 168,059 | 0,234024 |
| 17,03 | -7,38 | 39,77 | 36,665 | 39,28909 | 630,5623 | 505,6612 | 6,88584 | 0,071569 |
| 21,43 | 13,82 | 11,00 | 80,605 | 78,58932 | 354,5312 | 282,6877 | 4,062964 | 0,025007 |
| 16,35 | 33,62 | 24,77 | 88,94 | 76,659 | 737,8829 | 221,5035 | 150,8231 | 0,138082 |
| 19,13 | 16,88 | 7,91 | 95,57 | 79,33921 | 1142,034 | 308,4663 | 263,4386 | 0,169831 |
| 24,15 | 16,46 | 26,84 | 84,285 | 74,54634 | 506,6551 | 163,0816 | 94,84146 | 0,115544 |
| 10,07 | 10,30 | 35,06 | 45,825 | 44,62256 | 254,4344 | 294,2405 | 1,445861 | 0,02624 |
| 9,70 | 19,14 | 29,12 | 52,8 | 54,04514 | 80,56858 | 59,76613 | 1,550385 | 0,023582 |
| 20,62 | -3,12 | -3,19 | 71,215 | 74,23969 | 89,09472 | 155,3436 | 9,148766 | 0,042473 |
| 15,37 | -25,64 | 13,25 | 35,775 | 40,44312 | 676,052 | 455,0917 | 21,79135 | 0,130486 |
| 16,67 | 12,88 | 15,98 | 59,505 | 67,90428 | 5,157441 | 37,55576 | 70,54782 | 0,141152 |
| 2,92 | 15,70 | 22,34 | 43,82 | 45,97975 | 322,4179 | 249,5216 | 4,664509 | 0,049287 |
| 17,13 | 4,46 | 32,09 | 55,175 | 52,59596 | 43,5732 | 84,27311 | 6,651442 | 0,046743 |
| 11,20 | 4,90 | 19,58 | 51,43 | 52,07724 | 107,0397 | 94,06601 | 0,418916 | 0,012585 |
| 17,63 | 7,52 | 9,50 | 56,835 | 69,54504 | 24,41348 | 60,35797 | 161,5451 | 0,22363 |
| 25,65 | -2,36 | 10,07 | 77,645 | 73,83463 | 251,8252 | 145,4105 | 14,51892 | 0,049074 |
| 27,77 | 2,62 | 27,95 | 74,93 | 69,30786 | 173,0277 | 56,72889 | 31,60847 | 0,075032 |
| сумма | 3088,8 | 3088,8 | 15498,77 | 12845,67 | 2653,10 | 4,542562 |
Проверим выполнение равенства сумм. Так как 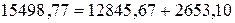 , оно выполнено. Следовательно, имеем
, оно выполнено. Следовательно, имеем 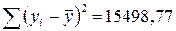

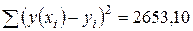 . То есть общая дисперсия равна
. То есть общая дисперсия равна 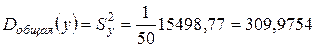 , факторная дисперсия равна
, факторная дисперсия равна 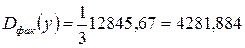 и остаточная дисперсия равна
и остаточная дисперсия равна 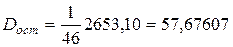 .
.
Найдем коэффициент множественной детерминации по трем формулам 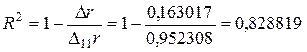 ,
, 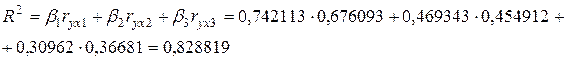
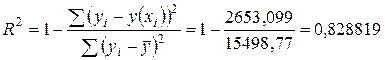
Все полученные коэффициенты детерминации равны, найдём коэффициент множественной корреляции 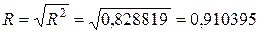
Проверим значимость уравнения регрессии через критерий 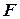 , для этого вычислим его двумя способами
, для этого вычислим его двумя способами 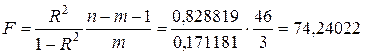 и
и 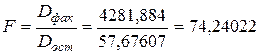 . Критическое значение критерия
. Критическое значение критерия 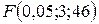 равно 2,806845 и, следовательно, уравнение регрессии в целом значимо. Найдём среднюю ошибку аппроксимации по формуле
равно 2,806845 и, следовательно, уравнение регрессии в целом значимо. Найдём среднюю ошибку аппроксимации по формуле 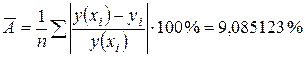 , она показывает неплохое качество описания реального изменения результативного признака уравнением регрессии. Формула скорректированного индекса множественного детерминации
, она показывает неплохое качество описания реального изменения результативного признака уравнением регрессии. Формула скорректированного индекса множественного детерминации
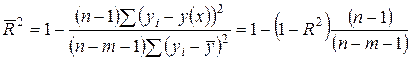 . Чем больше величина
. Чем больше величина 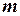 , сильнее различия
, сильнее различия 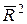 и
и  . Для рассматриваемого примера равна
. Для рассматриваемого примера равна 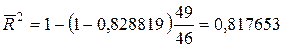 .
.
Частные уравнения регрессии.
На основе линейного уравнения множественной регрессии 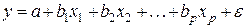
Можно найти частное уравнение регрессии по переменной  путем подстановки в него средних значений
путем подстановки в него средних значений 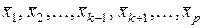 . В отличии от парной регрессии частные уравнения регрессии характеризуют изолированное влияние фактора на результат, при условии, что остальные факторы закреплены на неизменном уровне. Эффекты влияния других факторов присоединены в них к свободному члену уравнения регрессии. Это позволяет определять частные коэффициенты эластичности:
. В отличии от парной регрессии частные уравнения регрессии характеризуют изолированное влияние фактора на результат, при условии, что остальные факторы закреплены на неизменном уровне. Эффекты влияния других факторов присоединены в них к свободному члену уравнения регрессии. Это позволяет определять частные коэффициенты эластичности: 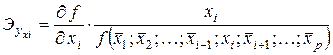 , где
, где 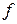 - функция определяющая уравнение множественной регрессии. Или средние по совокупности показатели эластичности
- функция определяющая уравнение множественной регрессии. Или средние по совокупности показатели эластичности 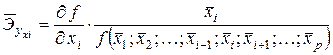 .Для линейной регрессии можно так же использовать формулы
.Для линейной регрессии можно так же использовать формулы 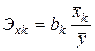 .
.
Найдём средние коэффициенты эластичности для рассматриваемого примера: 
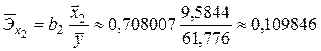
 .
.
Следовательно, наибольшее влияние на результат оказывает фактор 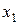 наименьшее
наименьшее 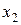 . Используя частные уравнения регрессии можно найти частные значения критерия
. Используя частные уравнения регрессии можно найти частные значения критерия 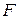 . И оценивать значимость не только уравнения в целом, но и каждого фактора включённого в регрессионную модель. Частный F-критерий построен на сравнении прироста факторной дисперсии, обусловленного влиянием дополнительно включённого фактора, с остаточной дисперсией на одну степень свободы по регрессионной модели в целом. Предположим, что оцениваем значимость влияния
. И оценивать значимость не только уравнения в целом, но и каждого фактора включённого в регрессионную модель. Частный F-критерий построен на сравнении прироста факторной дисперсии, обусловленного влиянием дополнительно включённого фактора, с остаточной дисперсией на одну степень свободы по регрессионной модели в целом. Предположим, что оцениваем значимость влияния 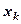 как дополнительно включённого в модель фактора. Используем следующую формулу:
как дополнительно включённого в модель фактора. Используем следующую формулу:
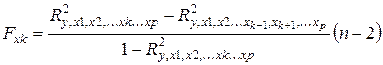
где: 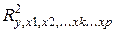 - коэффициент множественной корреляции для модели с полным набором факторов;
- коэффициент множественной корреляции для модели с полным набором факторов;
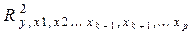 - тот же показатель, но без включения в модель фактора
- тот же показатель, но без включения в модель фактора  ;
;
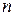 - число наблюдений.
- число наблюдений.
Продолжение примера.
5. Найти значения частных значений критерия 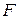 и определить значимость каждого фактора в отдельности.
и определить значимость каждого фактора в отдельности.
Найдем частные критерии 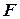 , для этого вычислим
, для этого вычислим 
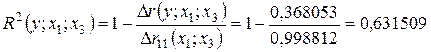
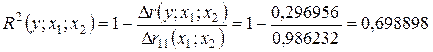
Тогда 
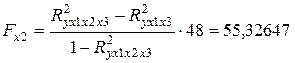
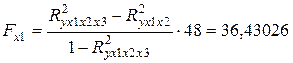
Критическое значение критерия 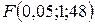 равно 4,042652 следовательно согласно критерию
равно 4,042652 следовательно согласно критерию 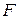 все факторы значимы, но наиболее значим первый фактор.
все факторы значимы, но наиболее значим первый фактор.
Частная корреляция.
Частные коэффициенты (индексы) корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включённых в уравнение регрессии. Показатели частной корреляции представляют собой отношение остаточной дисперсии за счёт включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель.
Пусть в уравнение простой регрессии добавили ещё один фактор 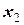 тогда чистое влияние этого фактора на результат
тогда чистое влияние этого фактора на результат  можно определить как
можно определить как 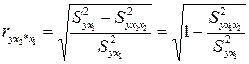 или
или  , соответственно
, соответственно 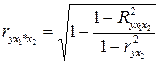 .если рассматривается регрессия с числом факторов
.если рассматривается регрессия с числом факторов 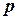 , то возможны частные коэффициенты корреляции не только первого, но и второго, третьего,…..,
, то возможны частные коэффициенты корреляции не только первого, но и второго, третьего,….., 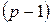 порядка, то есть влияние фактора
порядка, то есть влияние фактора 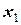 можно оценить при разных условиях независимости действий других факторов:
можно оценить при разных условиях независимости действий других факторов:
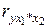 - при постоянном действии фактора
- при постоянном действии фактора 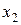 ;
;
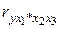 - при постоянном действии факторов
- при постоянном действии факторов 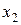 и
и 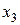 ;
;
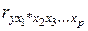 - при постоянном действии всех факторов включены[ в уравнение регрессии.
- при постоянном действии всех факторов включены[ в уравнение регрессии.
Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается. Соответственно коэффициенты парной корреляции называются коэффициентами нулевого порядка. Коэффициенты частной корреляции более высоких порядков можно определить через коэффициенты частной корреляции более низких порядков по рекуррентной формуле: 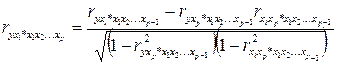 .
.
Дата добавления: 2016-02-09; просмотров: 908;
