Эконометрика - лекции 1 страница

Эконометрика (Econometrics) - совокупность методов анализа связей между различными экономическими показателями (факторами) на основании реальных статистических данных с использованием аппарата теории вероятностей и математической статистики. При помощи этих методов можно выявлять новые, ранее не известные связи, уточнять или отвергать гипотезы о существовании определенных связей между экономическими показателями, предлагаемые экономической теорией.

Экономисты используют количественные данные для наблюдения за ходом развития экономики, её анализа и прогнозов. Набор статистических методов, используемых для этих целей, называется в совокупности эконометрикой. Для успешного применения этих методов необходимо понимание процессов, породивших имеющиеся данные которые мы пытаемся исследовать. Поскольку наши модели неполны, а данные несовершенны, значительная часть эконометрики посвящена методам, которые могли работать с такими моделями и данными. Эконометрика как наука расположена где-то между экономикой, статистикой и математикой. Один из ответов на вопрос, что такое эконометрика, может звучать так: это наука, связанная с эмпирическим выводом экономических законов. То есть мы используем данные или наблюдения для того, чтобы получить количественные зависимости для экономических соотношений. Данные, как правило, не являются экспериментальными, так как в экономике мы не можем проводить (многократные) эксперименты.

Парная регрессия.

Спецификация модели.

Для описания количественных взаимосвязей между экономическими переменными в эконометрике используются методы регрессии.

В зависимости от количества факторов, включенных в уравнение регрессии, принято различать простую (парную) и множественную регрессии.

Простая регрессия представляет собой регрессию между двумя переменными - у и х, т. е. модель вида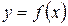

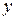— зависимая переменная (результативный признак);

х — независимая, или объясняющая, переменная (признак-фактор).

Множественная регрессия соответственно представляет собой регрессию результативного признака с двумя и большим числом факторов, т. е. модель вида .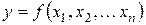

Любое эконометрическое исследование начинается со спецификации модели, т. е. с формулировки вида модели, исходя из соответствующей теории связи между переменными. Прежде всего, из всего круга факторов, влияющих на результативный признак, необходимо выделить наиболее существенно влияющие факторы. Парная регрессия достаточна, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной. В этом случае необходимо знать, какие остальные факторы предполагаются неизменными, возможно, в дальнейшем их придется учесть в модели и от простой регрессии перейти к множественной.

Уравнение простой регрессии характеризует связь между двумя переменными, которая проявляется как некоторая закономерность лишь в среднем в целом по совокупности наблюдений. В уравнении регрессии корреляционная по сути связь признаков представляется в виде функциональной связи, выраженной соответствующей математической функцией. Практически в каждом отдельном случае величина у складывается из двух слагаемых: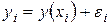

где - фактическое значение результативного признака;

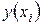- теоретическое значение результативного признака, найденное исходя из соответствующей математической функции связи у и х, т. е. из уравнения регрессии;

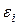- случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.

Случайная величина 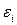называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели порождено тремя источниками: спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных.

К ошибкам спецификации будут относиться неправильный выбор той или иной математической функции и недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множественной.

Наряду с ошибками спецификации могут иметь место ошибки выборки, поскольку исследователь чаше всего имеет дело с выборочными данными при установлении закономерной связи между признаками. Ошибки выборки имеют место и в силу неоднородности данных в исходной статистической совокупности, что, как правило, бывает при изучении экономических процессов. Если совокупность неоднородна, то уравнение регрессии не имеет практического смысла. Для получения хорошего результата обычно исключают из совокупности единицы с аномальными значениями исследуемых признаков. И в этом случае результаты регрессии представляют собой выборочные характеристики.

Использование временной информации также представляет собой выборку из всего множества хронологических дат. Изменив временной интервал, можно получить другие результаты регрессии.

Наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя форму модели (вид математической формулы), а ошибки выборки — увеличивая объем исходных данных, то ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками.

Приведем один пример: в настоящее время органы государственной статистики получают балансы предприятий, достоверность которых никто не подтверждает. Последующее обобщение такой информации может содержать ошибки измерения. Исследуя, например, в качестве результативного признака прибыль предприятий, мы должны быть уверены, что предприятия показывают в отчетности адекватные реальной действительности величины.

Предполагая, что ошибки измерения сведены к минимуму, основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели.

В парной регрессии выбор вида математической функции 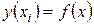может быть осуществлен тремя методами:

• графическим;

• аналитическим, т. е. исходя из теории изучаемой взаимосвязи;

• экспериментальным.

При изучении зависимости между двумя признаками графический метод подбора вида уравнения регрессии достаточно нагляден. Он основан на поле корреляции.

Значительный интерес представляет аналитический метод выбора типа уравнения регрессии. Он основан на изучении материальной природы связи исследуемых признаков.

При обработке информации на компьютере выбор вида уравнения регрессии обычно осуществляется экспериментальным методом, т. е. путем сравнения величины остаточной дисперсии 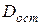, рассчитанной при разных моделях.

Если уравнение регрессии проходит через все точки корреляционного поля, что возможно только при функциональной связи, когда все точки лежат на линии регрессии, то фактические значения результативного признака совпадают с теоретическими, т. е. они полностью обусловлены влиянием фактора х. В этом случае остаточная дисперсия 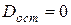. В практических исследованиях, как правило, имеет место некоторое рассеяние точек относительно линии регрессии. Оно обусловлено влиянием прочих не учитываемых в уравнении регрессии факторов. То есть, есть отклонения фактических данных от теоретических 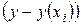. Величина этих отклонений лежит в основе расчета остаточной дисперсии: ; где: 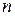-количество наблюдений; -число параметров при объясняющей переменной.

Чем меньше величина остаточной дисперсии, тем в меньшей мере наблюдается влияние прочих не учитываемых в уравнении регрессии факторов лучше уравнение регрессии подходит к исходным данным. При обработке статистических данных на компьютере перебираются разные математические функции в автоматическом режиме, и из них выбирается та, для которой остаточная дисперсия является наименьшей.

Если остаточная дисперсия оказывается примерно одинаковой для нескольких функций, то на практике предпочтение отдается более простым видам функций, ибо они в большей степени поддаются интерпретации и требуют меньшего объема наблюдений. Результаты многих исследований подтверждают, что число наблюдений должно в 6 - 7 раз превышать число рассчитываемых параметров при переменной х. Это означает, что искать линейную регрессию, имея менее 7 наблюдений, вообще не имеет смысла. Если вид функции усложняется, то требуется увеличение объема наблюдений, ибо каждый параметр при х должен рассчитываться хотя бы по 7 наблюдениям. Значит, если мы выбираем параболу второй степени 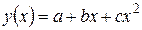, то требуется объем информации уже не менее 14 наблюдений. Учитывая, что эконометрические модели часто строятся по данным рядов динамики, ограниченным по протяженности (10, 20, 30 лет), при выборе спецификации модели предпочтительна модель с меньшим числом параметров при х.

Оценка параметров линейной регрессии.

Линейная регрессия находит широкое применение в эконометрике в виде четкой экономической интерпретации ее параметров. Задача линейной регрессии состоит в том, что по конкретной выборке 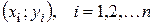, найти оценки и 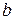неизвестных параметров и так, чтобы построенная линия 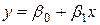являлась бы наилучшей в определенном смысле среди всех других прямых. То есть при нахождении уравнения вида .

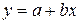Методом наименьших квадратов можно получить следующую формулу для нахождения параметра 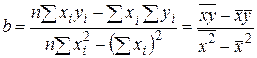. Параметр 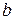называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Параметр находится по формуле .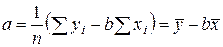

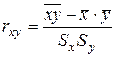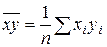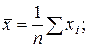
Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции , где: , 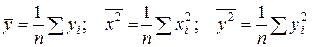; ; 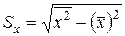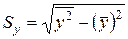. Следует иметь в виду, что величина коэффициента корреляции оценивает тесноту линейной связи рассматриваемых признаков. Поэтому близость абсолютной величины линейного коэффициента корреляции к нулю ещё не означает отсутствие связи между признаками. При иной спецификации модели связь между признаками может оказаться достаточно тесной. Используя коэффициент корреляции уравнение регрессии можно записать в виде 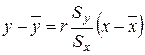, тогда получаем, что 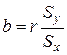и .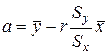

Оценка существенности уравнения регрессии.

После того как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.

Оценка значимости уравнения регрессии в целом дается с помощью -крите-рия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, т. е. 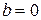, то есть фактор 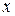не оказывает влияния на результат у.

Непосредственному расчету -критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение обшей суммы квадратов отклонений переменной у от среднего на две части — «объясненную» и «необъясненную»:

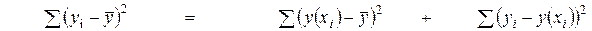
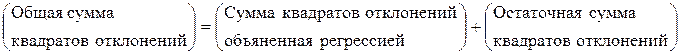
Общая сумма квадратов отклонений индивидуальных значений результативного признака у от среднего значения 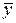вызвана влиянием множества причин. Условно разделим всю совокупность причин на две группы: изучаемый фактор х и прочие факторы. Если фактор не оказывает влияния на результат, то линия регрессии на графике параллельна оси Ох и 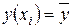. Тогда вся дисперсия результативного признака обусловлена воздействием прочих факторов и общая сумма квадратов отклонений совпадет с остаточной. Если же прочие факторы не влияют на результат, то у связан с х функционально и остаточная сумма квадратов равна нулю. В этом случае сумма квадратов отклонений, объясненная регрессией, совпадает с обшей суммой квадратов.

Поскольку не все точки поля корреляции лежат на линии регрессии, то всегда имеет место их разброс как обусловленный влиянием фактора х, т. е. регрессией у по х, так и вызванный действием прочих причин (необъясненная вариация). Пригодность линии регрессии для прогноза зависит от того, какая часть обшей вариации признака у приходится на объясненную вариацию. Очевидно, что если сумма квадратов отклонений, обусловленная регрессией, будет больше остаточной суммы квадратов, то уравнение регрессии статистически значимо и фактор 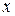оказывает существенное воздействие на результат у. Это равносильно тому, что коэффициент детерминации 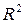, будет приближаться к единице.

Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим средний квадрат отклонений, или дисперсию на одну степень свободы: 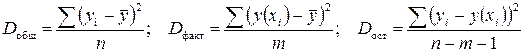, где: 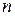- число наблюдений, - число параметров при независимой переменной.

Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчёте на одну степень свободы, получим величину - критерия: для проверки нулевой гипотезы .

Если нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Для 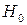необходимо опровержение, чтобы факторная дисперсия превышала остаточную в несколько раз. Для нахождения табличного значения - критерия по таблице задаётся уровень значимости 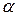число степеней свободы большей дисперсии равно , меньшей . Если вычисленное значение - критерия больше табличного нулевая гипотеза отклоняется и делается вывод о существенности связи.

Ранее показано 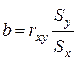или, так как 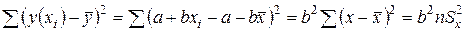, поэтому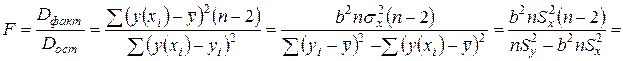 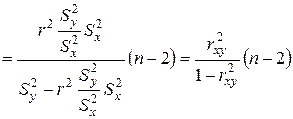следовательно .

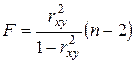Коэффициент детерминации характеризует долю дисперсии результативного признака 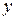, объясняемую регрессией, в общей дисперсии результативного признака: 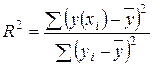. Для линейной зависимости 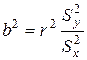, поэтому выполнено равенство 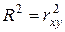покажем это 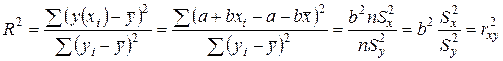. Следовательно, величина 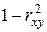характеризует долю дисперсии 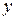, вызванную влиянием остальных не учтенных в модели факторов.

Пример 1. Имеется 15 пар статистических наблюдений

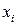
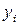
1) Для заданной выборки найти уравнение линейной регрессии.

2) Проверить равенство сумм.

3) Вычислить значение - критерия двумя способами.

4) Проверить значимость полученного уравнения регрессии.

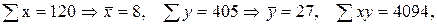
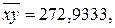
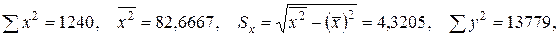
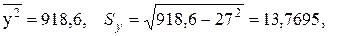
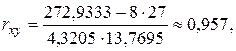
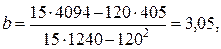
Решение: Найдём требуемые величины , тогда уравнение линейной регрессии имеет вид 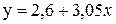. Для нахождения сумм составим таблицу

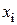
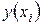
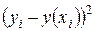
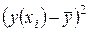
		5,65	2,7225		455,8225
		8,7	1,69		334,89
		11,75	10,5625		232,5625
		14,8	23,04		148,84
		17,85	4,6225		83,7225
		20,9	16,81		37,21
		23,95	25,5025		9,3025
		30,05	1,1025		9,3025
		33,1	65,61		37,21
		36,15	14,8225		83,7225
		39,2	3,24		148,84
		42,25	10,5625		232,5625
		45,3	7,29		334,89
		48,35	2,7225		455,8225
			239,3		2604,7

Из таблицы следует: 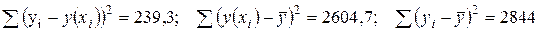, то есть равенство сумм выполняется 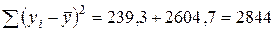. Вычислим 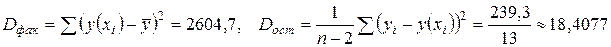, тогда значение - критерия равно 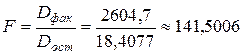используем другое соотношение 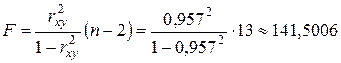. Отсюда следует, что вычисления проведены верно и уравнение значимо, так как критическое значение - критерия при уровне значимости 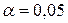равно 4,67.

Значимость коэффициентов регрессии

Проверить значимость оценок коэффициентов регрессии – значит установить, достаточна ли величина оценки для статистически обоснованного вывода о том, что коэффициенты регрессии отличны от нуля. Для этого проверяют гипотезу о равенстве нулю коэффициентов регрессии, соблюдая предпосылки нормальной регрессии.

Стандартная ошибка коэффициента регрессии . Величина стандартной ошибки коэффициента совместно с 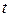- распределением Стьюдента при 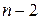степенях свободы применяется для проверки существенности коэффициентов регрессии и для расчета его доверительных интервалов. Для оценки значимости регрессии его величина сравнивается с его стандартной ошибкой, то есть определяется фактическое значение 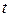-критерия Стьюдента: 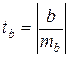, которое затем сравнивается с табличным значением при определённом уровне значимости 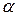и числе степеней свободы .

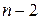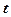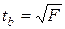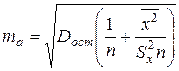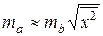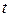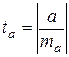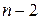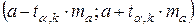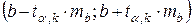Возможен и другой подход нахождения фактического значения -критерия: , следовательно . Стандартная ошибка параметра определяется по формуле или процедура оценивания существенности данного параметра не отличается от рассмотренной ранее. Вычисляется -критерий: ; его величина сравнивается с табличным при степенях свободы. Доверительные интервалы для коэффициентов регрессии и , где 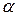уровень значимости, 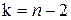- число степеней свободы, - критическое значение критерия Стьюдента (двусторонний). Поскольку коэффициент регрессии в эконометрических исследованиях имеет чёткую экономическую интерпретацию, то доверительные границы для коэффициентов регрессии не должны содержать противоречивых результатов, например . Такого рода запись указывает, что истинное значение коэффициентов регрессии одновременно содержит положительные и отрицательные значения, чего не может быть.

Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции 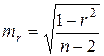. Расчетное значение критерия Стьюдента определяется как 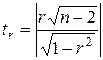. Данная формула свидетельствуют, что в парной линейной регрессии 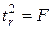, так как 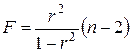. Кроме того 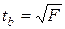. Следовательно 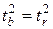. Таким образом, проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверки гипотезы о существенности линейного уравнения регрессии.

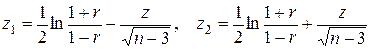Доверительный интервал для коэффициента корреляции находится по формуле , где и .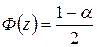

Продолжение примера 1

5) Проверить значимость коэффициентов регрессии и корреляции при уровне значимости .

6) Построить при уровне значимости 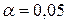доверительные интервалы для коэффициентов регрессии и коэффициента корреляции.

Решение. Найдём , , 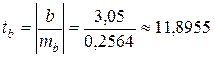используя другую формулу, найдём 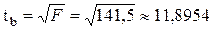по уровню значимости 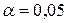найдём 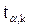равное 2,16, следовательно, коэффициент регрессии значим. Стандартную ошибку параметра определим по формуле , , 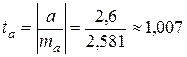сравнивая с критическим значением, получаем, что параметр 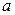не значим.