Эконометрика - лекции 2 страница

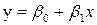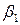
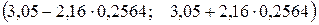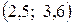Доверительные интервалы для коэффициентов регрессии имеют вид: для или ; для 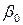получаем 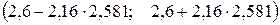или 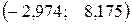. Проверим значимость коэффициента корреляции, для этого найдем, 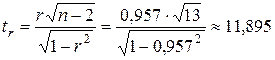то есть коэффициент корреляции значим. Запишем доверительный интервал для коэффициента корреляции, для этого вычислим 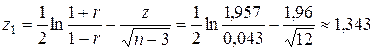, 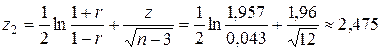. Следовательно, доверительный интервал имеет вид .

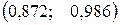Интервалы прогноза по линейному

уравнению регрессии.

В прогнозных расчётах по уравнению регрессии определяется предсказываемое значение как точечный прогноз . Однако точечный прогноз явно не реален поэтому он дополняется расчётом стандартной ошибки 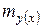и интервальной оценкой 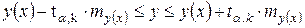. Для построения формулы для нахождения стандартной ошибки используем уравнение регрессии 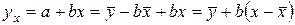. Отсюда вытекает, что стандартная ошибка 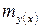зависит от ошибки и ошибки коэффициента регрессии 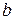. То есть 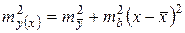. 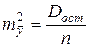Но и 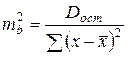, отсюда следует .

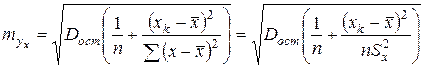Рассмотренная формула стандартной ошибки предсказываемого среднего значения 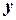при заданном значение 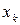характеризует ошибку положения линии регрессии. Величина стандартной ошибки 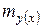, как видно из формулы достигает минимума при 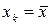, и возрастает по мере удаления от этого значения.

Фактические значения 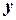варьируются около среднего значения 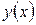. Индивидуальные значения 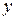могут отклонятся от 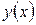на величину случайной ошибки 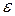, дисперсия которой оценивается остаточной дисперсией. Поэтому ошибка предсказываемого индивидуального значения должна включать не только стандартную ошибку 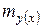но и случайную ошибку 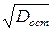. Средняя ошибка прогнозируемого индивидуального значения находится по формуле: .

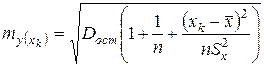Продолжение примера 1

7) Найти доверительный интервал для прогнозного значения при .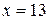

Решение. Найдём стандартную ошибку 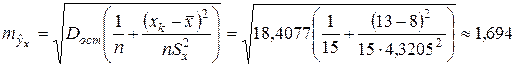, прогнозное значение 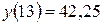, следовательно, интервал имеет вид 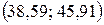. Эмпирическое значение равно 39 попадает в этот интервал. Найдём среднюю ошибку прогнозируемого индивидуального значения, которая находится по формуле: 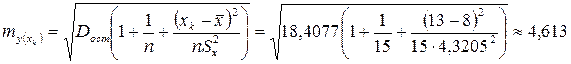. Тогда доверительный интервал имеет вид .

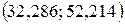Средняя ошибка аппроксимации.

Фактические значения результативного признака отличаются теоретических, рассчитанных по уравнению регрессии, т. е. 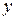и 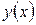. Чем меньше это отличие, тем ближе теоретические значения к эмпирическим данным, лучше качество модели. Величина отклонений фактических и расчетных значений результативного признака по каждому наблюдению представляет ошибку аппроксимации. Их число соответствует объему совокупности. В отдельных случаях ошибка аппроксимации может оказаться равной нулю.

Поскольку может быть как величиной положительной, так и отрицательной, то ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю. Отклонения можно рассматривать как абсолютную ошибку аппроксимации, а 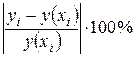- как относительную ошибку аппроксимации. Чтобы иметь общее суждение о качестве модели из относительных отклонений наблюдению, определяют среднюю ошибку аппроксимации: 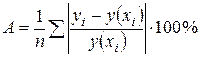. Если 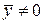то можно использовать иное определение средней ошибки аппроксимации 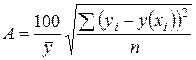. Второе определение используется тогда когда какое-либо значение 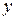равно нулю.

Продолжение примера 1

З) Найти среднюю ошибку аппроксимации.

Для этого составим расчётную таблицу

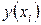
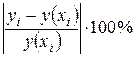
		5,65	29,20354
		8,7	14,94253
		11,75	27,65957
		14,8	32,43243
		17,85	12,04482
		20,9	19,61722
		23,95	21,08559
			25,92593
		30,05	3,494176
		33,1	24,4713
		36,15	10,65007
		39,2	4,591837
		42,25	7,692308
		45,3	5,960265
		48,35	3,412616
			243,1842

Следовательно средняя ошибка аппроксимации равна 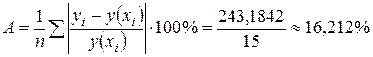, что указывает на не совсем точное описание реального процесса.

Нелинейная регрессия.

Различают два класса нелинейных регрессий:

1. регрессии, нелинейные относительно включённых в анализ объясняющих переменных, но линейные по оцениваемым параметрам;

2. регрессии, нелинейные по оцениваемым параметрам.

Основные функции, относящиеся к первому классу: 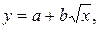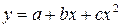, 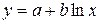и 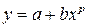при заданном значении .

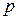Второй класс представлен функциями вида: показательная 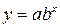, степенная 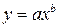, обратная .

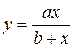Все эти функции могут быть приведены к линейному виду. Рассмотрим методы нахождения параметров для указанных зависимостей.

Для функции 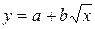, замена переменных 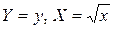сводит эту функцию к линейному виду 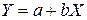, для функции 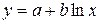замена переменных 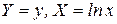, для функции 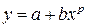новые переменные 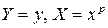. Для параболы 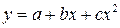можно составить систему уравнений для нахождения параметров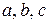 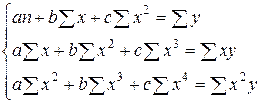, зависимость 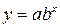путём логарифмирования можно привести к виду 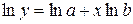тогда вводя новые переменные 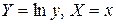найдем значения параметров 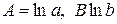потенцируя находим значения исходных параметров 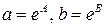. Зависимость 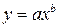также путём логарифмирования можно привести к виду 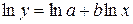, новые переменные 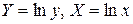находим значения параметров 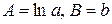, исходные параметры равны 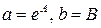. Зависимость 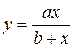перевернем каждую из дробей получим 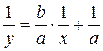вводя новые переменные 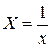и 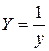найдём значения 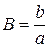и 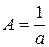, исходные параметры равны 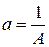и .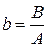

Пример 2. Задано десять пар наблюдений

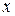
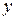
Требуется:1) Методом наименьших квадратов определить зависимость, имеющую наименьшую дисперсии из возможных. Предложенные зависимости имеют вид: .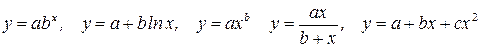

Решение:

1. Определим параметры зависимости 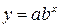. Для этого перейдем к условным вариантам по формулам 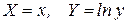и составим расчетную таблицу.

№
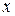
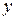
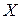
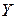
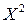
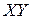
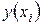
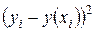
				1,3863		2,7726	1,4619	6,444
				1,0986		3,2958	1,7933	1,456
				0,6931		2,7726	2,2005	0,040
							2,7002	2,891
							3,3133	5,351
				1,0986		7,6903	4,0656	1,135
				1,6094		12,8755	4,9887	0,0001
				1,9459		17,5132	6,1215	0,772
				2,3979		23,9790	7,5114	12,170
				2,7726		30,4985	9,2169	46,010
				13,0025		101,3974	43,372	76,27

Найдем параметры линейного уравнения 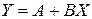по формулам ,

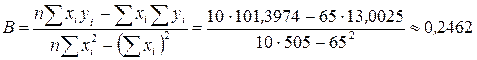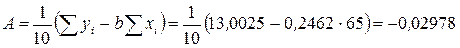. Найдем параметры нелинейной регрессии по формулам 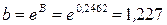, 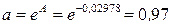. По полученному уравнению 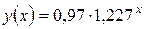находим расчётные значения 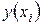и записываем в таблицу. Затем находим остаточную дисперсию .

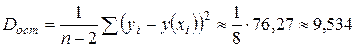Определим параметры зависимости 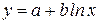. Для этого перейдем к условным вариантам по формулам 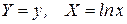и составим расчётную таблицу

№
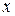
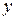
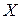
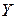
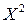
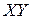
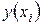
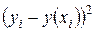
			0,6931		0,4804	2,7726	-0,3502	18,9244
			1,0986		1,2069	3,2958	1,8170	1,3994
			1,3863		1,9218	2,7726	3,3547	1,8353
			1,6094		2,5903	1,6094	4,5474	12,5844
			1,7918		3,2104	1,7918	5,5219	20,4483
			1,9459		3,7866	5,8377	6,3459	11,1952
			2,0779		4,3241	10,3972	7,0597	4,2422
			2,1972		4,8277	15,3805	7,6892	0,4750
			2,3026		5,3019	25,3284	8,2524	7,5494
			2,3979		5,7499	38,3663	8,7618	52,3911
			17,5023		33,4002	107,5525		131,0446

Найдем параметры линейного уравнения 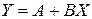по формулам ,

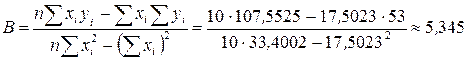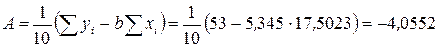. Найдем параметры нелинейной регрессии по формулам 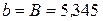, 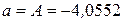. По полученному уравнению 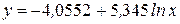находим расчётные значения 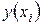и записываем в таблицу. Затем находим остаточную дисперсию .

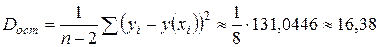Определим параметры зависимости 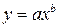. Для этого перейдем к условным вариантам по формулам 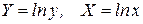и составим расчётную таблицу

№
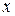
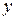
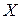
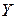
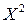
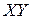
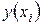
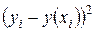
			0,6931	1,3863	0,4804	0,9609	1,5237	6,1323
			1,0986	1,0986	1,2069	1,2069	2,1347	0,7487
			1,3863	0,6931	1,9218	0,9609	2,7117	0,5065
			1,6094		2,5903		3,2647	5,1287
			1,7918		3,2104		3,7992	7,8354
			1,9459	1,0986	3,7866	2,1378	4,3188	1,7394
			2,0779	1,6094	4,3241	3,3467	4,8261	0,0302
			2,1972	1,9459	4,8277	4,2756	5,3228	2,8131
			2,3026	2,3979	5,3019	5,5214	5,8102	26,9337
			2,3979	2,7726	5,7499	6,6484	6,2895	94,2933
			17,5023	13,0025	33,4002	25,0586	40,0014	146,1613

Найдем параметры линейного уравнения 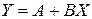по формулам ,

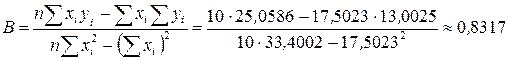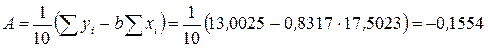. Найдем параметры нелинейной регрессии по формулам 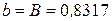, 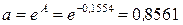. По полученному уравнению 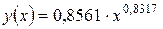находим расчётные значения 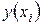и записываем в таблицу. Затем находим остаточную дисперсию .

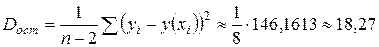Определим параметры зависимости 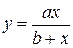. Для этого перейдем к условным вариантам по формулам 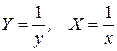и составим расчётную таблицу

№
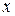
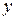
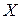
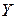
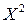
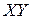
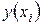
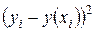
			0,5	0,25	0,25	0,125	2,1182	3,541
			0,3333	0,3333	0,1111	0,1111	2,3424	0,4327
			0,25	0,5	0,0625	0,125	2,4733	0,2241
			0,2		0,04	0,2	2,5591	2,431
			0,1667		0,0278	0,1667	2,6197	2,6236
			0,1429	0,3333	0,0204	0,0476	2,6648	0,1124
			0,125	0,2	0,0156	0,025	2,6996	5,2917
			0,1111	0,1429	0,0123	0,0159	2,7274	18,2555
			0,1	0,0909	0,01	0,0090	2,7499	68,0634
			0,0909	0,0625	0,0083	0,0057	2,7687	175,0669
			2,0198	3,9129	0,558	0,8310	25,7234	276,0418

Найдем параметры линейного уравнения 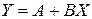по формулам ,

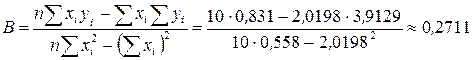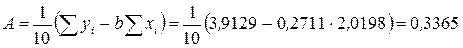. Найдем параметры нелинейной регрессии по формулам 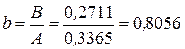, 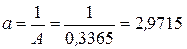. По полученному уравнению 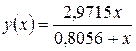находим расчётные значения 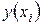и записываем в таблицу. Затем находим остаточную дисперсию .

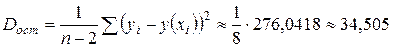Определим параметры зависимости 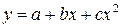. Для этого составим систему уравнений 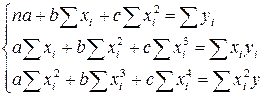. Для нахождения требуемых сумм составим расчётную таблицу

№
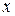
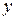
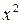
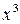
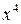
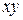
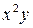
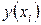
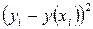
								4,5363	0,2877
								2,5848	0,1724
								1,4288	0,3263
								1,0681	0,0046
								1,5030	0,2530
								2,7333	0,0711
								4,7591	0,0580
								7,5803	0,3368
								11,197	0,0388
								15,609	0,1528
									1,7015

Система уравнений имеет вид: 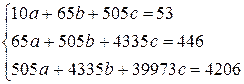. Для решения этой системы используем правило Крамера. Вычислим определители: 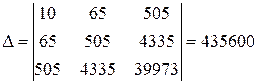; ; 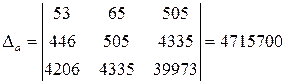; 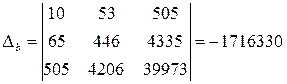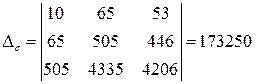. Вычисление определителей проводим в Microsoft Excel используя функцию «МОПРЕД». По правилу Крамера: 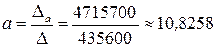, , 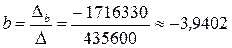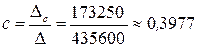. По полученному уравнению 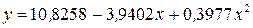находим расчётные значения 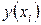и записываем в таблицу. Затем находим остаточную дисперсию 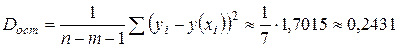. Наименьшую остаточную дисперсию имеет уравнение регрессии 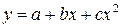. Следовательно, оно является лучшим для описания характера изменения .