Эконометрика - лекции 3 страница
Среди нелинейных функций, которые могут, приведены к линейному виду, в эконометрических исследованиях широко используется степенная функция 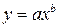 . Связано это с тем, что параметр
. Связано это с тем, что параметр 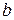 в ней имеет чёткое экономическое обоснование – он является коэффициентом эластичности и показывает, на сколько процентов в среднем изменится результат, если фактор изменится на 1%. Для расчёта коэффициента эластичности используют формулу
в ней имеет чёткое экономическое обоснование – он является коэффициентом эластичности и показывает, на сколько процентов в среднем изменится результат, если фактор изменится на 1%. Для расчёта коэффициента эластичности используют формулу 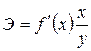 . В силу того, что для некоторых зависимостей коэффициент эластичности зависит от соответствующего значения
. В силу того, что для некоторых зависимостей коэффициент эластичности зависит от соответствующего значения 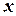 , то обычно рассчитывается средний коэффициент эластичности
, то обычно рассчитывается средний коэффициент эластичности 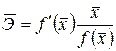 .
.
Продолжение примера 2. 2) Найти средний коэффициент эластичности для зависимости 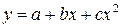 .
.
Решение. Так как 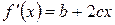 , то при
, то при  получаем
получаем 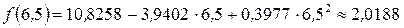 и
и 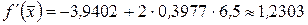 то средний коэффициент эластичности равен
то средний коэффициент эластичности равен 
Корреляция для нелинейной регрессии.
Уравнение нелинейной регрессии, так же как и в линейной зависимости, дополняется показателем корреляции, а именно индексом корреляции 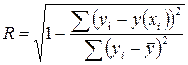 . Величина данного показателя находится в границах
. Величина данного показателя находится в границах 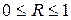 , чем ближе к единице, тем теснее связь рассматриваемых признаков, тем более надёжно найденное уравнение регрессии. Поскольку в расчёте индекса корреляции используется отношении факторной и общей суммы квадратов отклонений, то
, чем ближе к единице, тем теснее связь рассматриваемых признаков, тем более надёжно найденное уравнение регрессии. Поскольку в расчёте индекса корреляции используется отношении факторной и общей суммы квадратов отклонений, то 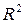 имеет тот же смысл, что и коэффициент детерминации. В специальных исследованиях величину
имеет тот же смысл, что и коэффициент детерминации. В специальных исследованиях величину 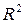 для нелинейных связей называют индексом детерминации.
для нелинейных связей называют индексом детерминации.
Оценка существенности индекса корреляции проводится, так же как и оценка надёжности коэффициента корреляции. Индекс детерминации используется для проверки существенности в целом уравнения нелинейной регрессии по 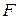 - критерию Фишера:
- критерию Фишера: 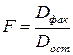 , где
, где 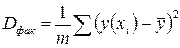 и
и  . Второй способ нахождения этого значения через индекс детерминации
. Второй способ нахождения этого значения через индекс детерминации 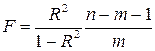 , где:
, где: 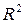 - индекс детерминации;
- индекс детерминации; 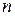 - число наблюдений;
- число наблюдений;  - число параметров при переменных
- число параметров при переменных 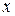 . Величина
. Величина  характеризует число степеней свободы для факторной дисперсии,
характеризует число степеней свободы для факторной дисперсии, 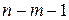 число степеней для остаточной дисперсии. Значения критерия
число степеней для остаточной дисперсии. Значения критерия 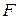 вычисленные по этим двум формулам совпадают если выполнено равенство сумм.
вычисленные по этим двум формулам совпадают если выполнено равенство сумм.
Продолжение примера 2. 3) Найти индекс корреляции, значение критерия 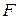 и среднюю ошибку аппроксимации.
и среднюю ошибку аппроксимации.
Решение: Для нахождения требуемых величин составим расчётную таблицу
| № | 
| 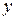
| 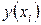
| 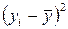
| 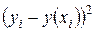
| 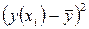
| 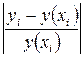
|
| 4,5363 | 1,69 | 0,2877 | 0,58314 | 0,118236 | |||
| 2,5848 | 5,29 | 0,1724 | 7,372048 | 0,16061 | |||
| 1,4288 | 10,89 | 0,3263 | 14,98628 | 0,399788 | |||
| 1,0681 | 18,49 | 0,0046 | 17,90829 | 0,06383 | |||
| 1,5030 | 18,49 | 0,2530 | 14,41698 | 0,334677 | |||
| 2,7333 | 5,29 | 0,0711 | 6,587778 | 0,097561 | |||
| 4,7591 | 0,09 | 0,0580 | 0,292583 | 0,050621 | |||
| 7,5803 | 2,89 | 0,3368 | 5,199782 | 0,076554 | |||
| 11,197 | 32,49 | 0,0388 | 34,77425 | 0,017591 | |||
| 15,609 | 114,49 | 0,1528 | 106,2774 | 0,025044 | |||

| 210,1 | 1,7015 | 208,3985 | 1,344512 |
Тогда индекс корреляции равен 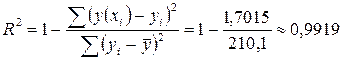 . Если выполнено равенство сумм то для нахождения индекса корреляции можно использовать формулу
. Если выполнено равенство сумм то для нахождения индекса корреляции можно использовать формулу 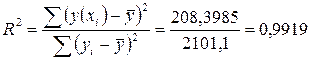 . Равенство сумм в данном примере
. Равенство сумм в данном примере 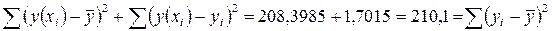 выполнено. Значение критерия найдем по формуле
выполнено. Значение критерия найдем по формуле 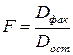 . Где
. Где 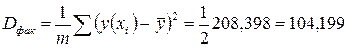 , остаточная дисперсия найдена была ранее и равна
, остаточная дисперсия найдена была ранее и равна 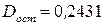 . Следовательно, значение критерия
. Следовательно, значение критерия 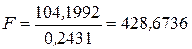 . По другой формуле имеем
. По другой формуле имеем 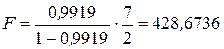 . Критическое значение критерия равно
. Критическое значение критерия равно 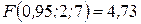 . Так как наблюдаемое значение больше критического то уравнение регрессии в целом значимо. Средняя ошибка аппроксимации составит
. Так как наблюдаемое значение больше критического то уравнение регрессии в целом значимо. Средняя ошибка аппроксимации составит 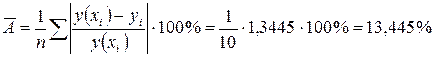 .
.
Индекс детерминации 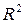 можно сравнивать с коэффициентом детерминации
можно сравнивать с коэффициентом детерминации 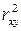 для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина коэффициента
для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина коэффициента 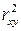 меньше индекса детерминации
меньше индекса детерминации 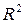 . Близость этих показателей означает, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию. Практически если разность величин
. Близость этих показателей означает, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию. Практически если разность величин 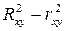 не превышает 0,1, то предположение о линейной форме связи считается оправданным. В противном случае проводится оценка существенности различия
не превышает 0,1, то предположение о линейной форме связи считается оправданным. В противном случае проводится оценка существенности различия 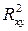 и
и 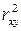 вычисленных по одним и тем же исходным данным, через
вычисленных по одним и тем же исходным данным, через 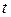 -критерий Стьюдента:
-критерий Стьюдента: 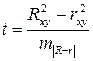 , где
, где  ошибка разности между
ошибка разности между 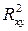 и
и 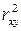 определяемая по формуле
определяемая по формуле 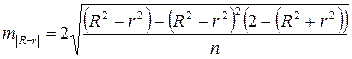 . Если
. Если 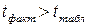 , то различия между рассматриваемыми показателями корреляции существенны и замена нелинейной регрессии уравнением линейной функции невозможна. Практически, если величина
, то различия между рассматриваемыми показателями корреляции существенны и замена нелинейной регрессии уравнением линейной функции невозможна. Практически, если величина 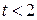 , то различия между
, то различия между 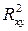 и
и 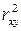 несущественны и, следовательно, возможно применение линейной регрессии, даже если есть предположения о некоторой нелинейности рассматриваемых соотношений признаков факторов и результата.
несущественны и, следовательно, возможно применение линейной регрессии, даже если есть предположения о некоторой нелинейности рассматриваемых соотношений признаков факторов и результата.
Продолжение примера 2. 4) Возможно применить линейную зависимость вместо параболы.
Решение: Найдём коэффициент корреляции по формуле 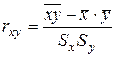 , где:
, где: 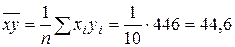 ;
; 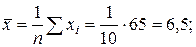
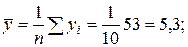
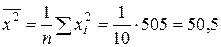 ;
; 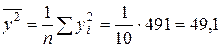 ;
; 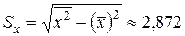 ;
; 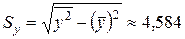 . Тогда
. Тогда 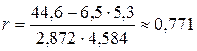 . Найдём ошибку разности
. Найдём ошибку разности  . Расчётное значение критерия равно
. Расчётное значение критерия равно 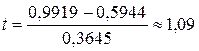 . Полученное значение меньше критического
. Полученное значение меньше критического 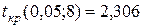 следовательно при необходимости можно параболическую зависимость линейной.
следовательно при необходимости можно параболическую зависимость линейной.
Множественная регрессия.
Спецификация модели.
Парная регрессия может дать хороший результат при моделировании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Поведение отдельных экономических переменных контролировать нельзя, т. е. не удается обеспечить равенство всех прочих условий для оценки влияния одного исследуемого фактора. В этом случае следует попытаться выявить влияние других факторов, введя их в модель, т. е. построить уравнение множественной регрессии. Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах и целого ряда других вопросов эконометрики. В настоящее время множественная регрессия — один из наиболее распространенных методов в эконометрике. Основная цель множественной регрессии — построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель. Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели. Суть проблемы спецификации включает в себя два круга вопросов: отбор факторов и выбор вида уравнения регрессии. Их решение при построении модели множественной регрессии имеет некоторую специфику.
Отбор факторов при построении множественной регрессии.
Включение в уравнение множественной регрессии того или иного набора факторов связано прежде всего с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям.
1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность (например, в модели урожайности качество почвы задается в виде баллов).
2. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи.
Включение в модель факторов с высокой интеркорреляцией, когда 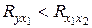 для зависимости
для зависимости 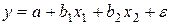 может привести к нежелательным последствиям - система нормальных уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии. Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются не интерпретируемыми. Так, в уравнении
может привести к нежелательным последствиям - система нормальных уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии. Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются не интерпретируемыми. Так, в уравнении 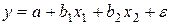 предполагается, что факторы
предполагается, что факторы 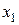 и
и 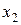 независимы друг от друга, т. е.
независимы друг от друга, т. е. 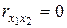 . Тогда можно говорить, что параметр
. Тогда можно говорить, что параметр 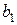 измеряет силу влияния фактора
измеряет силу влияния фактора 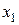 на результат у при неизменном значении фактора
на результат у при неизменном значении фактора 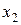 . Если же
. Если же 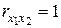 , то с изменением фактора
, то с изменением фактора 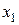 , фактор
, фактор 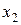 не может оставаться неизменным. Отсюда
не может оставаться неизменным. Отсюда 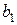 и
и  нельзя интерпретировать как показатели раздельного влияниях
нельзя интерпретировать как показатели раздельного влияниях 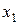 и
и 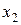 на у.
на у.
Включаемые во множественную регрессию факторы должны объяснить вариацию независимой переменной. Если строится модель с набором р факторов, то для нее рассчитывается показатель детерминации R , который фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии р факторов. Влияние других, не учтенных в модели факторов оценивается, как 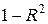 с соответствующей остаточной дисперсией
с соответствующей остаточной дисперсией 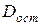 .
.
При дополнительном включении в регрессию 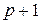 фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться. Если же этого не происходит, и данные показатели практически мало отличаются друг от друга, то включаемый в анализ фактор
фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться. Если же этого не происходит, и данные показатели практически мало отличаются друг от друга, то включаемый в анализ фактор 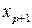 не улучшает модель и практически является лишним фактором. Так, если для регрессии, включающей пять факторов, коэффициент детерминации составил 0,857, и включение шестого фактора дало коэффициент детерминации 0,858, то вряд ли целесообразно дополнительно включать в модель этот фактор. Насыщение модели лишними факторами не только не снижает величину остаточной дисперсии и не увеличивает показатель детерминации, но и приводит к статистической не значимости параметров регрессии по
не улучшает модель и практически является лишним фактором. Так, если для регрессии, включающей пять факторов, коэффициент детерминации составил 0,857, и включение шестого фактора дало коэффициент детерминации 0,858, то вряд ли целесообразно дополнительно включать в модель этот фактор. Насыщение модели лишними факторами не только не снижает величину остаточной дисперсии и не увеличивает показатель детерминации, но и приводит к статистической не значимости параметров регрессии по 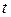 -критерию Стьюдента.
-критерию Стьюдента.
Таким образом, хотя теоретически регрессионная модель позволяет учесть любое число факторов, практически в этом нет необходимости. Отбор факторов производится на основе качественного теоретико-экономического анализа. Однако теоретический анализ часто не позволяет однозначно ответить на вопрос о количественной взаимосвязи рассматриваемых признаков и целесообразности включения фактора в модель. Поэтому отбор факторов обычно осуществляется в две стадии: на первой подбираются факторы исходя из сущности проблемы; на второй - на основе матрицы показателей корреляции определяют 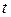 -статистики для параметров регрессии.
-статистики для параметров регрессии.
Коэффициенты интеркорреляции (т. е. корреляции между объясняющими переменными) позволяют исключать из модели дублирующие факторы. Считается, что две переменных явно коллинеарны, т, е. находятся между собой в линейной зависимости, если 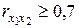 .
.
Поскольку одним из условий построения уравнения множественной регрессии является независимость действия факторов, т. е. 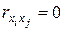 . Коллинеарность факторов нарушает это условие. Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании проявляется специфика множественной регрессии как метода исследования комплексного воздействия факторов в условиях их независимости друг от друга. Пусть, например, при изучении зависимости
. Коллинеарность факторов нарушает это условие. Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании проявляется специфика множественной регрессии как метода исследования комплексного воздействия факторов в условиях их независимости друг от друга. Пусть, например, при изучении зависимости 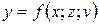 матрица парных коэффициентов корреляции оказалась следующей:
матрица парных коэффициентов корреляции оказалась следующей:
| y | x | z | v | |
| y | ||||
| x | 0,8 | |||
| z | 0,7 | 0,8 | ||
| v | 0,6 | 0,5 | 0,2 |
Очевидно, что факторы х и z дублируют друг друга. В анализ целесообразно включить фактор z, а не х, так как хотя корреляция z с результатом у слабее, чем корреляция фактора х с у (  ), но зато слабее межфакторная корреляция
), но зато слабее межфакторная корреляция 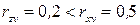 . Поэтому в данном случае в уравнение множественной регрессии включаются факторы z, v.
. Поэтому в данном случае в уравнение множественной регрессии включаются факторы z, v.
По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, т. е. имеет место совокупное воздействие факторов друг на друга. Наличие мультиколлинеарности факторов может означать, что некоторые факторы будут всегда действовать в унисон. В результате вариация в исходных данных перестает быть полностью независимой, и нельзя оценить воздействие каждого фактора в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов (МНК).
Если рассматривается регрессия 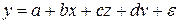 , то для расчета параметров, применяя МНК, предполагается равенство
, то для расчета параметров, применяя МНК, предполагается равенство 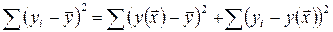
При независимости факторов друг от друга факторная сумма квадратов отклонений равна сумме квадратов отклонений обусловленной влиянием каждого фактора.
Если же факторы интеркоррелировакы, то данное равенство нарушается.
Включение в модель мультиколинеарных факторов нежелательно в силу следующих последствий:
· затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом» виде, ибо факторы коррелированны;
· параметры линейной регрессии теряют экономический смысл;
· оценки параметров ненадежны, обнаруживают большие стандартные ошибки и меняются с изменением объема наблюдений (не только по величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования.
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами.
Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной матрицей, поскольку все недиагональные элементы 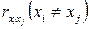 были бы равны нулю. Так, для включающего три объясняющих переменных уравнения
были бы равны нулю. Так, для включающего три объясняющих переменных уравнения 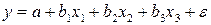 матрица коэффициентов корреляции между факторами имела бы определитель, равный единице
матрица коэффициентов корреляции между факторами имела бы определитель, равный единице 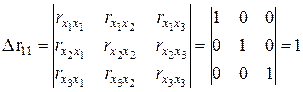 . Если же, наоборот, между факторами существует полная линейная зависимость и все коэффициенты корреляции равны единице, то определитель такой матрицы равен нулю:
. Если же, наоборот, между факторами существует полная линейная зависимость и все коэффициенты корреляции равны единице, то определитель такой матрицы равен нулю:  . Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
. Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
Оценка значимости мультиколлинеарности факторов может быть проведена методом испытания гипотезы о независимости переменных 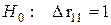 . Доказано, что величина
. Доказано, что величина 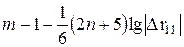 имеет приближенное распределение
имеет приближенное распределение  с
с 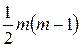 степенями свободы, где
степенями свободы, где 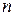 - число наблюдений,
- число наблюдений, 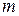 - число факторов. Если фактическое значение
- число факторов. Если фактическое значение  превосходит табличное, то гипотеза
превосходит табличное, то гипотеза  отклоняется. Это означает, что
отклоняется. Это означает, что 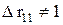 , недиагональные ненулевые коэффициенты корреляции указывают на коллинеарность факторов. Мультиколлинеарность считается доказанной. Через значение определителя межфакторной корреляции можно найти переменные, ответственные за мультиколлинеарность факторов. Для этого в качестве зависимой переменной рассматривается каждый из факторов. Чем ближе значение определителя межфакторной корреляции к нулю, тем сильнее проявляется мультиколлинеарность факторов. Сравнивая между собой эти значения, можно выделить переменные, ответственные за мультиколлинеарность, следовательно, можно решать проблему отбора факторов, оставляя в уравнении факторы с минимальной величиной коэффициента множественной детерминации.
, недиагональные ненулевые коэффициенты корреляции указывают на коллинеарность факторов. Мультиколлинеарность считается доказанной. Через значение определителя межфакторной корреляции можно найти переменные, ответственные за мультиколлинеарность факторов. Для этого в качестве зависимой переменной рассматривается каждый из факторов. Чем ближе значение определителя межфакторной корреляции к нулю, тем сильнее проявляется мультиколлинеарность факторов. Сравнивая между собой эти значения, можно выделить переменные, ответственные за мультиколлинеарность, следовательно, можно решать проблему отбора факторов, оставляя в уравнении факторы с минимальной величиной коэффициента множественной детерминации.
Оценка параметров уравнения множественной регрессии.
Параметры уравнения множественной регрессии оцениваются по МНК. Используя его, составляется система линейных уравнений, решение которой позволяет находить оценки параметров регрессии. Возможен и другой подход к определению параметров множественной регрессии, когда на основе матрицы парных коэффициентов корреляции строится уравнение регрессии в стандартизованном масштабе: 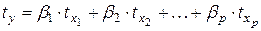 , где:
, где: 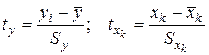 - стандартизованные переменные, для которых среднее значение равно нулю, а среднее квадратическое отклонение равно единице. Параметры
- стандартизованные переменные, для которых среднее значение равно нулю, а среднее квадратическое отклонение равно единице. Параметры 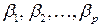 можно найти МНК.
можно найти МНК.
В парной зависимости стандартизованный коэффициент регрессии есть линейный коэффициент корреляции. Во множественной регрессии коэффициенты 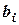 связаны со стандартизованными коэффициентами
связаны со стандартизованными коэффициентами 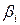 зависимостью
зависимостью 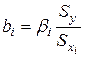 . Это позволяет от уравнения регрессии в стандартизованном масштабе
. Это позволяет от уравнения регрессии в стандартизованном масштабе 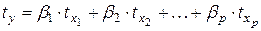 переходить к уравнению регрессии в натуральном масштабе переменных
переходить к уравнению регрессии в натуральном масштабе переменных 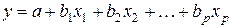 . Параметр
. Параметр 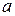 равен
равен 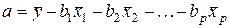 .
.
Пример 3. Множественная регрессия
Исходные данные
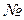
| 
| 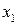
| 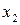
| 
| 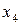
|
| 59,69 | 24,00 | 5,3 | 24,56 | 29,69 | |
| 53,71 | 6,75 | 16,08 | 28,01 | 24,59 | |
| 81,44 | 19,32 | 17,06 | 22,46 | 37,65 | |
| 74,58 | 19,60 | 0,76 | 10,79 | 20,63 | |
| 36,29 | 2,47 | -9,96 | 5,9 | -4,77 | |
| 95,19 | 24,67 | 17,96 | 13,4 | 43,62 | |
| 82,96 | 28,13 | 4,8 | -3,1 | 32,95 | |
| 58,24 | 14,83 | 15,58 | 17,87 | 31,22 | |
| 82,74 | 27,57 | 37,52 | 25,7 | 63,01 | |
| 58,13 | 11,88 | 28,08 | 21,2 | 38,63 | |
| 62,21 | 20,48 | 30,56 | 35,09 | 48,95 | |
| 47,34 | 7,90 | 10,36 | 31,07 | 19,13 | |
| 89,80 | 18,15 | 14,26 | 8,87 | 34,39 | |
| 85,29 | 29,40 | 29,08 | 21,08 | 55,68 | |
| 14,78 | -6,85 | 2,06 | 31,61 | -2,56 | |
| 65,04 | 18,25 | 0,66 | 19,31 | 19,69 | |
| 45,04 | 11,40 | 2,16 | 18,62 | 14,44 | |
| 69,31 | 12,93 | 20,74 | 16,19 | 34,39 | |
| 58,71 | 9,62 | 10,14 | 13,28 | 20,75 | |
| 85,92 | 17,95 | 15,08 | 35,67 | ||
| 60,61 | 17,88 | 8,3 | 33,26 | 27,92 | |
| 60,61 | 22,25 | -0,28 | 30,41 | 22,88 | |
| 57,80 | 24,43 | -0,22 | 31,43 | 25,10 | |
| 64,33 | 18,62 | -0,92 | 18,71 | 19,51 | |
| 22,90 | -4,52 | 5,22 | 31,37 | 2,70 | |
| 50,81 | -2,32 | 12,54 | 2,39 | 11,40 | |
| 59,16 | 17,97 | -0,56 | 17,93 | 19,09 | |
| 59,47 | 23,35 | 3,26 | 25,46 | 27,43 | |
| 56,22 | 10,50 | 8,1 | 20,33 | 20,20 | |
| 68,92 | 23,00 | 18,3 | 34,94 | 40,97 | |
| 49,62 | 12,93 | 7,62 | 23,99 | 22,54 | |
| 51,42 | 9,88 | 14,36 | 23,81 | 25,63 | |
| 54,19 | 8,02 | 5,1 | -1,69 | 14,91 | |
| 55,40 | 16,97 | 9,4 | 11,99 | 25,75 | |
| 36,67 | 17,03 | -7,38 | 39,77 | 10,82 | |
| 80,61 | 21,43 | 13,82 | 35,52 | ||
| 88,94 | 16,35 | 33,62 | 24,77 | 50,93 | |
| 95,57 | 19,13 | 16,88 | 7,91 | 35,21 | |
| 84,29 | 24,15 | 16,46 | 26,84 | 39,07 | |
| 45,83 | 10,07 | 10,3 | 35,06 | 20,77 | |
| 52,80 | 9,70 | 19,14 | 29,12 | 30,34 | |
| 71,22 | 20,62 | -3,12 | -3,19 | 19,41 | |
| 35,78 | 15,37 | -25,64 | 13,25 | -7,70 | |
| 59,51 | 16,67 | 12,88 | 15,98 | 30,71 | |
| 43,82 | 2,92 | 15,7 | 22,34 | 19,18 | |
| 55,18 | 17,13 | 4,46 | 32,09 | 22,41 | |
| 51,43 | 11,20 | 4,9 | 19,58 | 17,36 | |
| 56,84 | 17,63 | 7,52 | 9,5 | 25,57 | |
| 77,65 | 25,65 | -2,36 | 10,07 | 23,07 | |
| 74,93 | 27,77 | 2,62 | 27,95 | 31,36 |
1) Проверить факторы на мультиколлинеарность, выявить фактор ответственный за мультиколлинеарность и удалить его.
Дата добавления: 2016-02-09; просмотров: 1159;
