Эконометрика - лекции 5 страница
При двух факторах и 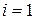 данная формула примет вид:
данная формула примет вид:  .
.
Продолжение примера.
6. Найти частные значения коэффициентов корреляции и определить их значимость.
Проверим значимость факторов на основе критерия Стьюдента, для этого вычислим частные коэффициенты корреляции. Найдём: 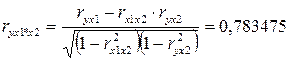


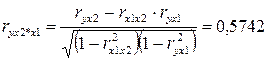
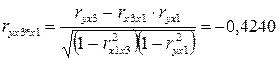
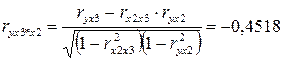
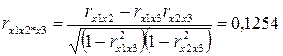
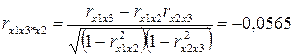

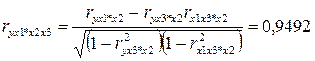
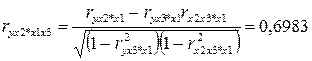
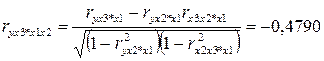
Проверим значимость коэффициентов корреляции по формуле 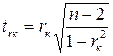 . Получим
. Получим 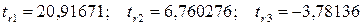 . Полученные значения по модулю больше критического значения равного 2,010635. Следовательно, все коэффициенты регрессии значимы, но наиболее значимый первый фактор.
. Полученные значения по модулю больше критического значения равного 2,010635. Следовательно, все коэффициенты регрессии значимы, но наиболее значимый первый фактор.
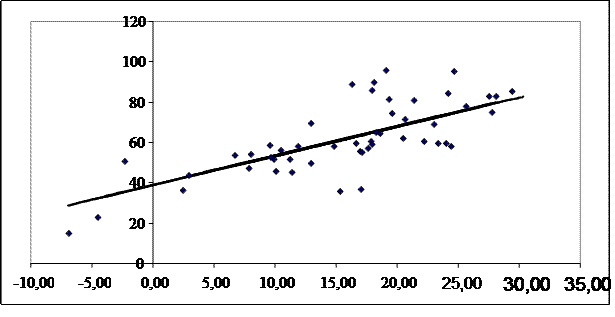
Наиболее значимым фактором является первый, найдем уравнение частной регрессии для этого фактора 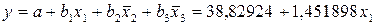 . Построим поле регрессии для этого фактора и линию регрессии.
. Построим поле регрессии для этого фактора и линию регрессии.
Найдём прогнозные значения факторов по формулам 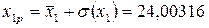 ,
, 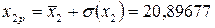 ,
, 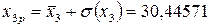 . Найдем прогнозное значение результативного признака по формуле
. Найдем прогнозное значение результативного признака по формуле 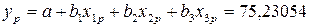 . Найдём ошибку прогноза
. Найдём ошибку прогноза 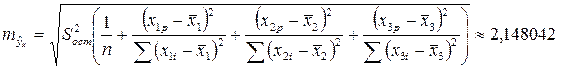 , доверительный интервал для прогнозного значения найдем по формуле
, доверительный интервал для прогнозного значения найдем по формуле  или
или 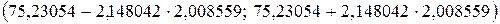 окончательно
окончательно 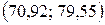 .
.
ОДНОМЕРНЫЕ ВРЕМЕННЫХ РЯДЫ
ОСНОВНЫЕ ЭЛЕМЕНТЫ ВРЕМЕННОГО РЯДА
Можно построить эконометрическую модель, используя два типа исходных данных:
• данные, характеризующие совокупность различных объектов в определенный момент (период) времени;
• данные, характеризующие один объект за ряд последовательных моментов (периодов) времени. Модели, построенные по данным первого типа, называются пространственными моделями. Модели, построенные на основе второго типа данных, называются моделями временных рядов.
Временной ряд — это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени. Каждый уровень временного ряда формируется под воздействием большого числа факторов, которые условно можно подразделить на три группы: первая группа формирует тенденцию; вторая, формирует циклические колебания; остальные случайные колебания.
При различных сочетаниях в изучаемом явлении или процессе этих факторов зависимость уровней ряда от времени может принимать различные формы.
Во-первых, большинство временных рядов экономических показателей имеют тенденцию, характеризующую долговременное совокупное воздействие множества факторов на динамику изучаемого показателя. Очевидно, что эти факторы, взятые в отдельности, могут оказывать разнонаправленное воздействие на исследуемый показатель. Однако в совокупности они формируют его возрастающую или убывающую тенденцию
Во-вторых, изучаемый показатель может быть подвержен циклическим колебаниям. Эти колебания могут носить сезонный характер, поскольку экономическая деятельность ряда отраслей экономики зависит от времени года (например, цены на сельскохозяйственную продукцию в летний период выше, чем в зимний; уровень безработицы в курортных городах в зимний период выше по сравнению с летним). При наличии больших массивов данных за длительные промежутки времени можно выявить циклические колебания, связанные с общей динамикой конъюнктуры рынка.
Некоторые временные ряды не содержат тенденции и циклической компоненты, а каждый следующий их уровень образуется как сумма среднего уровня ряда и некоторой (положительной или отрицательной) случайной компоненты.
Очевидно, что реальные данные не следуют целиком и полностью из каких-либо описанных выше моделей. Чаще всего они содержат все три компоненты. Каждый их уровень формируется под воздействием тенденции, сезонных колебаний и случайной компоненты. В большинстве случаев фактический уровень временного ряда можно представить как сумму или произведение трендовой, циклической и случайной компонент. Модель, в которой временной ряд представлен как сумма перечисленных компонент, называется аддитивной моделью временного ряда. Модель, в которой временной ряд представлен как произведение перечисленных компонент, называется мультипликативной моделью временного ряда. Основная задача эконометрического исследования отдельного временного ряда — выявление и придание количественного выражения каждой из перечисленных выше компонент с тем, чтобы использовать полученную информацию для прогнозирования будущих значений ряда или при построении моделей взаимосвязи двух или более временных рядов.
АВТОКОРРЕЛЯЦИЯ УРОВНЕЙ ВРЕМЕННОГО РЯДА
И ВЫЯВЛЕНИЕ ЕГО СТРУКТУРЫ
При наличии во временном ряде тенденции и циклических колебаний значения каждого последующего уровня ряда зависят от предыдущих. Корреляционную зависимость между последовательными уровнями временного ряда называют автокорреляцией уровней ряда.
Количественно ее можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени. Число периодов, на которые сдвигается ряд, называют лагом. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается.
Отметим два важных свойства коэффициента автокорреляции. Во-первых, он строится по аналогии с линейным коэффициентом корреляции и таким образом характеризует тесноту только линейной связи текущего и предыдущего уровней ряда. Поэтому по коэффициенту автокорреляции можно судить о наличии линейной (или близкой к линейной) тенденции. Для некоторых временных рядов, имеющих сильную нелинейную тенденцию (например, параболу второго порядка или экспоненту), коэффициент автокорреляции уровней исходного ряда может приближаться к нулю.
Во-вторых, по знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда. Большинство временных рядов экономических данных содержит положительную автокорреляцию уровней, однако при этом могут иметь убывающую тенденцию.
Последовательность коэффициентов автокорреляции уровней первого, второго и т. д. порядков называют автокорреляционной функцией временного ряда. График зависимости ее значений от величины лага (порядка коэффициента автокорреляции) называется коррелограммой.
Анализ автокорреляционной функции и коррелограммы позволяет определить лаг, при котором автокорреляция наиболее высокая, а следовательно, и лаг, при котором связь между текущим и предыдущими уровнями ряда наиболее тесная, т. е. при помощи анализа автокорреляционной функции и коррелограммы можно выявить структуру ряда.
Если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка т, ряд содержит циклические колебания с периодичностью в тмоментов времени. Если ни один из коэффициентов автокорреляции не является значимым, можно сделать одно из двух предположений относительно структуры этого ряда: либо ряд не содержит тенденции и циклических колебаний. Либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ. Поэтому коэффициент автокорреляции уровней и автокорреляционную функцию целесообразно использовать для выявления во временном ряде наличия или отсутствия трендовой компоненты и циклической (сезонной) компоненты.
Рассмотрим пример. Пусть имеются условные данные об объёмах потребления электроэнергии жителями региона за 16 кварталов.
| t | ||||||||||||||||
| у | 4,4 | 7,2 | 4,8 | 5,6 | 6,4 | 6,6 | 7,0 | 10,8 |
Построим график
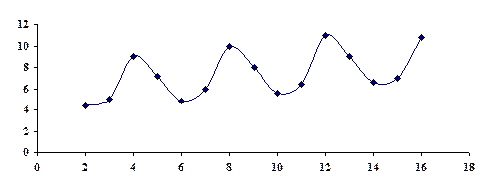
Из анализа графика видно, что в данном временном ряде есть тенденция. Хотя 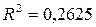 невелик.
невелик.
Найдем коэффициенты корреляции уровней.
| n | ||||||||
| r | 0,165 | -0,567 | 0,114 | 0,983 | 0,119 | -0,722 | -0,003 | 0,974 |
И её график имеет вид 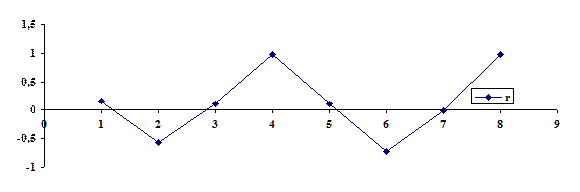
Анализ коррелограммы позволяет сделать вывод о наличии сезонных колебаний периодичностью в четыре квартала.
МОДЕЛИРОВАНИЕ ТЕНДЕНЦИИ ВРЕМЕННОГО РЯДА
Одним из наиболее распространенных способов моделирования тенденции временного ряда является построение аналитической функции, характеризующей зависимость уровней времени, или тренда. Этот способ называют аналитическим выравниванием временного ряда.
Поскольку зависимость от времени может принимать разные формы, для ее формализации можно использовать различные виды функций. Для построения трендов чаще всего применяются следующие функции:
• линейный тренд:  ;
;
• гипербола:  ;
;
• экспоненциальный тренд:  ;
;
• тренд в форме степенной функции 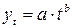 ;
;
• парабола второго и более высоких порядков: 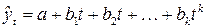
Параметры каждого из перечисленных выше трендов можно определить обычным МНК, используя в качестве независимой переменной время 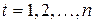 , а в качестве зависимой переменной — фактические уровни временного ряда
, а в качестве зависимой переменной — фактические уровни временного ряда  . Для нелинейных трендов предварительно проводят стандартную процедуру линеаризации.
. Для нелинейных трендов предварительно проводят стандартную процедуру линеаризации.
Существует несколько способов определения типа тенденции. К числу наиболее распространенных способов относя качественный анализ изучаемого процесса, построение и визуальный анализ графика, зависимости уровней ряда от времен расчет некоторых основных показателей динамики. В этих же целях можно использовать и коэффициенты автокорреляции уровней ряда. Тип тенденции можно определить путем сравнения: коэффициентов автокорреляции первого порядка, рассчитанных по исходным и преобразованным уровням ряда. Если времена имеет линейную тенденцию, то его соседние уровни 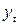 и
и 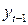 тесно коррелируют. В этом случае коэффициент автокорреляции первого порядка уровней исходного ряда должен быть высоким. Если временной ряд содержит нелинейную тенденцию, например, в форме экспоненты, то коэффициент автокорреляции первого порядка по логарифмам уровней исходного ряда будет выше, чем соответствующий коэффициент, рассчитанный по уровням ряда. Чем сильнее выражена нелинейная тенденция в изучаемом временном ряде, тем в большей степени будут различаться значения указанных коэффициентов.
тесно коррелируют. В этом случае коэффициент автокорреляции первого порядка уровней исходного ряда должен быть высоким. Если временной ряд содержит нелинейную тенденцию, например, в форме экспоненты, то коэффициент автокорреляции первого порядка по логарифмам уровней исходного ряда будет выше, чем соответствующий коэффициент, рассчитанный по уровням ряда. Чем сильнее выражена нелинейная тенденция в изучаемом временном ряде, тем в большей степени будут различаться значения указанных коэффициентов.
Выбор наилучшего уравнения в случае, если ряд содержит нелинейную тенденцию, можно осуществить путем перебора основных форм тренда, расчета по каждому уравнению скорректированного коэффициента детерминации 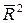 и выбора уравнения тренда с максимальным значением скорректированного коэффициента детерминации. Реализация этого метода относительно проста при компьютерной обработке данных.
и выбора уравнения тренда с максимальным значением скорректированного коэффициента детерминации. Реализация этого метода относительно проста при компьютерной обработке данных.
МОДЕЛИРОВАНИЕ СЕЗОННЫХ И ЦИКЛИЧЕСКИХ КОЛЕБАНИЙ.
Существуют несколько подходов к анализу временных рядов, содержащих сезонные или циклические колебания.
Простейший подход – расчет значений сезонной компоненты методом скользящей средней и построение аддитивной или мультипликативной модели временного ряда. Общий вид аддитивной модели: 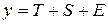 .
.
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой ( 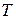 ), сезонной (
), сезонной (  ) и случайной (
) и случайной ( 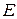 ) компонент. Общий вид мультипликативной модели выглядит так
) компонент. Общий вид мультипликативной модели выглядит так 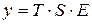
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой ( 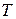 ) сезонной (S) и случайной (Е) компонент. Выбор одной из двух моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянными различных циклов. Если амплитуда сезонных колебаний тает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.
) сезонной (S) и случайной (Е) компонент. Выбор одной из двух моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянными различных циклов. Если амплитуда сезонных колебаний тает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.
Построение аддитивной и мультипликативной моделей сводится к расчету значений Т, S и Е для каждого уровня ряда. При этом существуют два подхода. Первый основан на выравнивании методом скользяще средней. При этом выделяются следующие этапы:
1. Выравнивание исходного ряда методом скользящей средней.
2. Расчет значений сезонной компоненты S.
3. Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных (Т+ Е) в аддитивной или ( 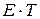 ) в мультипликативной модели.
) в мультипликативной модели.
4. Аналитическое выравнивание уровней (Т+ Е) или ( 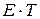 ) и расчет значений Т с использованием полученного уравнения тренда.
) и расчет значений Т с использованием полученного уравнения тренда.
5. Расчет полученных по модели значений (Т+ S) или ( 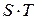 ).
).
6. Расчет абсолютных и/или относительных ошибок.
Если полученные значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни ряда и в дальнейшем использовать временной ряд ошибок 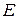 для анализа взаимосвязи исходного ряда и других временных рядов.
для анализа взаимосвязи исходного ряда и других временных рядов.
Второй метод основан на введении фиктивных переменных которые могут принимать только два значения. Количество этих переменных определяется периодом циклических колебаний.
Подробнее методику построения каждой из модели рассмотрим на примерах.
Первый. По данным примера
| t | ||||||||||||||||
| у | 4,4 | 7,2 | 4,8 | 5,6 | 6,4 | 6,6 | 7,0 | 10,8 |
Построить аддитивную модель временного ряда.
Решение. Введем фиктивные переменные. Так как наибольшее значение имеет коэффициент автокорреляции четвертого порядка то, вводим три фиктивные переменные. Получаем многофакторную модель. Фиктивные переменные принимают значения 0 или 1. Период единиц равен четырём.
Составим таблицу
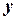
| 
| 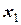
| 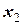
| 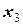
| 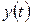
|
| 6,425 | |||||
| 4,4 | 4,225 | ||||
| 4,975 | |||||
| 9,075 | |||||
| 7,2 | 7,175 | ||||
| 4,8 | 4,975 | ||||
| 5,725 | |||||
| 9,825 | |||||
| 7,925 | |||||
| 5,6 | 5,725 | ||||
| 6,4 | 6,475 | ||||
| 10,575 | |||||
| 8,675 | |||||
| 6,6 | 6,475 | ||||
| 7,225 | |||||
| 10,8 | 11,325 |
По этой многофакторной модели получаем уравнение множественной регрессии 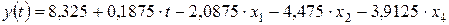 . После построения графика видно, что различие между эмпирическими и расчётными значениями мало.
. После построения графика видно, что различие между эмпирическими и расчётными значениями мало.
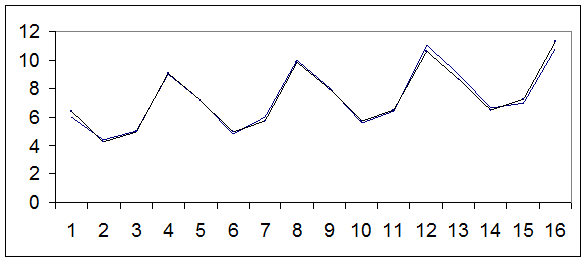
На это указывает и остаточная сумма 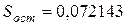 и
и 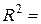 0,984952.
0,984952.
Пример. Построить мультипликативную модель по следующим данным:

| ||||||||||||||||
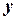
|
Построим график.
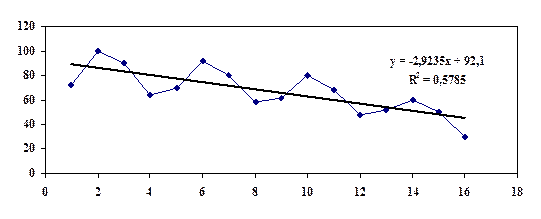
Из анализа графика видно наличие тренда (линейного) с уравнением 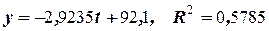 . Колебания заухают, следовательно, применяем мультипликативную модель. Проведём расчёт оценки сезонной компоненты методом скользящей средней.
. Колебания заухают, следовательно, применяем мультипликативную модель. Проведём расчёт оценки сезонной компоненты методом скользящей средней.

| 
| Итого за 4 квартала | Скользящая средняя за 4 квартала | Центрированная скользящая средняя | Оценка сезонной компоненты |
| - | |||||
| 81,5 | 81,25 | 1,108 | |||
| 0,8 | |||||
| 77,75 | 0,91 | ||||
| 76,5 | 75,75 | 1,215 | |||
| 1,081 | |||||
| 71,5 | 0,811 | ||||
| 68,5 | 0,905 | ||||
| 65,75 | 1,217 | ||||
| 64,5 | 63,25 | 1,075 | |||
| 59,5 | 0,807 | ||||
| 54,75 | 0,95 | ||||
| 52,5 | 50,25 | 1,194 | |||
Взаимопогашаемость сезонных воздействий в мультипликативной модели выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в цикле, в нашем примере 4.
Составим таблицу. Расчет сезонной компоненты в мультипликативной модели.
| Показатели | Год | № квартала | |||
| I | II | III | IV | ||
| - | - | 1,108 | 0,8 | ||
| 0,91 | 1,215 | 1,081 | 0,811 | ||
| 0,905 | 1,217 | 1,075 | 0,807 | ||
| 0,95 | 1,194 | - | - | ||
| Итого за квартал | 2,765 | 3,626 | 3,264 | 2,418 | |
Средняя оценка
сезонной компоненты 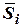
| 0,922 | 1,209 | 1,088 | 0,806 | |
Скорректированная сезонная
компонента 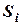
| 0,913 | 1,202 | 1,082 | 0,803 |
Где 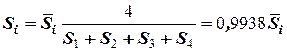
Таблица. Расчёт выравненых значений 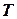 и ошибок
и ошибок 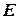 в мультипликативной модели.
в мультипликативной модели.

| 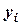
| 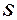
| 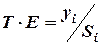
| 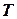
| 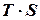
| 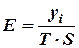
| 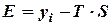
| 
|
| 0,913 | 78,86 | 87,8 | 80,16 | 0,898 | -8,16 | 66,66 | ||
| 1,202 | 83,19 | 85,03 | 102,2 | 0,978 | -2,20 | 4,86 | ||
| 1,082 | 83,18 | 82,25 | 1,011 | 1,0 | 1,0 | |||
| 0,803 | 79,7 | 79,48 | 63,82 | 1,003 | 0,18 | 0,03 | ||
| 0,913 | 76,67 | 76,7 | 70,03 | 1,000 | -0,03 | 0,00 | ||
| 1,202 | 76,54 | 73,93 | 88,86 | 1,035 | 3,14 | 9,85 | ||
| 1,082 | 73,94 | 71,15 | 76,99 | 1,039 | 3,01 | 9,08 | ||
| 0,803 | 72,23 | 68,38 | 54,91 | 1,056 | 3,09 | 9,57 | ||
| 0,913 | 67,91 | 65,6 | 59,9 | 1,035 | 2,10 | 4,43 | ||
| 1,202 | 66,56 | 62,83 | 75,52 | 1,059 | 4,48 | 20,08 | ||
| 1,082 | 62,85 | 50,05 | 64,98 | 1,047 | 3,02 | 9,14 | ||
| 0,803 | 59,78 | 57,28 | 45,99 | 1,044 | 2,01 | 4,03 | ||
| 0,913 | 56,96 | 54,50 | 49,76 | 1,045 | 2,24 | 5,02 | ||
| 1,202 | 49,92 | 51,73 | 62,18 | 0,965 | -2,18 | 4,73 | ||
| 1,082 | 46,21 | 48,95 | 52,97 | 0,944 | -2,97 | 8,79 | ||
| 0,803 | 37,36 | 46,18 | 37,08 | 0,809 | -7,08 | 50,12 |
Уравнение тренда имеет вид 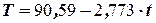 , коэффициент детерминации
, коэффициент детерминации 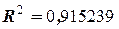 .
.
Построим график
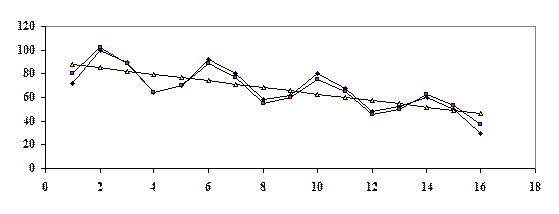
ИЗУЧЕНИЕ ВЗАИМОСВЯЗЕЙ ПО ВРЕМЕННЫМ РЯДАМ
СПЕЦИФИКА СТАТИСТИЧЕСКОЙ ОЦЕНКИ ВЗАИМОСВЯЗИ
Дата добавления: 2016-02-09; просмотров: 1062;
