Закон достаточного основания и формально-логические законы
Закон достаточного основания выражает требование доказательности и обоснованности мысли. Согласно этому закону,всякая истинная мысль должна быть обоснована другими мыслями, истинность которых уже доказана. Мысли (суждения), которые приводятся для обоснования истинности других мыслей, называются логическим основанием, а мысль (суждение), которая вытекает из других как из основания, называется логическим следствием. Логическую связь между основанием и следствием необходимо отличать от причинно-следственной связи, которая является выражением объективных отношений между предметами материального мира, в то время как логическое отношение основания и следствия выражает связь между высказываниями. Закон достаточного основания имеет важное теоретическое и практическое значение. Фиксируя внимание на требовании указания аргументов – оснований, обладающих достаточной силой доказательности, этот закон помогает отделить истину от лжи и тем самым прийти к верным выводам.
Формально-логические законы – это законы нормативного мышления. Соблюдение требований законов логики предохраняет мышление от логических ошибок и гарантирует получение истинного знания при условии, если исходное знание будет истинным.
Литература:
1. Арно А., Николь П. Логика, или искусство мыслить. М., 2006.
2. Асмус В.Ф. Учение логики о доказательстве и опровержении.
М., 2005.
3. Войшвилло Е.К. Понятие как форма мышления. М., 2008.
4. Гетманова А.Д. Логика. М., 2006.
5. Ивлев Ю.В. Логика. М., 2007.
6. Кириллов В.И., Старченко А.А. Логика. М., 2008.
7. Логика. Минск, 2006.
8. Свинцов В.И. Логика. М., 2007.
МОСКОВСКИЙ ГУМАНИТАРНО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА ОБЩЕГУМАНИТАРНЫХ И СОЦИАЛЬНО-ЭКНОМИЧЕСКИХ ДИСЦИПЛИН
Тема 3: Виды понятий. Логическая характеристика по объему и содержанию.
Учебные цели:
Дать учащимся общую характеристику понятий, рассмотреть и разграничить виды понятий по логическим характеристикам объема и содержания. Научит студентов логическим операциям с понятиями и операциям над классами. Рассмотреть основные законы логики классов и дать определение понятий по логическим признакам.
Вопросы:
1. Общая характеристика понятий.
2. Виды понятий. Логическая характеристика по объему и содержанию.
3. Отношения между понятиями по объему.
4. Логические операции с понятиями. Операции над классами (объемами понятий).
5. Основные законы логики классов.
6. Определение понятий.
Автор фондовой лекции:
Преподаватель кафедры ОГ и СЭД,
К.c.н. Тоторкулова М.М.
Рецензенты:
1. Доктор философских наук, профессор Сергодеева Е.А.
2. Доктор социологических наук, профессор Асеев Ю.А.
Лекция обсуждена и одобрена на заседании кафедры Общегуманитарных и социально-экономических дисциплин.
Протокол № от «____» ____________ 20__ г.
I
Понятие – это форма мысли, посредством которой предметы выделяются и обобщаются по существенным признакам. Понять нечто, т. е. составить понятие о предмете, это значит выразить сущность этого предмета. Этим понятие отличается от других познавательных форм – ощущения, восприятия, представления, которые не обладают такой обобщающей и абстрагирующей силой и, следовательно, в своем содержании не могут выразить закономерностей.
Как логическая форма понятие характеризуется двумя важнейшими параметрами – содержанием и объемом.
Содержание понятия – это совокупность существенных признаков предметов, на основании которых они выделяются и обобщаются.
Объем понятия – это предмет или совокупность предметов, обладающих признаками, составляющими содержание понятия.
Совокупность предметов, охватываемая объемом понятия, называется логическим классом, или множеством, а отдельный предмет объема понятия – элементом класса (множества).
Класс (множество) может включать в себя подклассы, или подмножества. Например, класс городов включает в себя подкласс городов России, класс рек – подкласс рек Сибири и т.д.
Понятие, из объема которого происходит выделение подкласса, называется родовым, или родом; понятие, объем которого выделяется из родового понятия – видовым, или видом (например, «наука» – родовое понятие, «юриспруденция» – видовое).
Содержание и объем понятия тесно связаны друг с другом. Эта связь выражается в законе обратного отношения между объемом и содержанием, согласно которому увеличение содержания понятия ведет к уменьшению его объема и наоборот. Или иначе: если объем одного понятия включает в себя объем другого понятия, то содержание первого понятия является частью содержания второго.
II
1. По объему понятия делятся на единичные и общие. Единичные – это такие понятия, объем которых составляет один элемент. Например, понятия «Александр Сергеевич Пушкин», «созвездие Большой Медведицы» и др.
Общими называются такие понятия, объем которых составляет два и более элемента. Например, понятия «человек», «животное», «логическая операция».
2. Понятия делятся на разделительные и собирательные. Разделительные – такие понятия, в объеме которых каждый индивидуальный предмет мыслится как элемент класса. Например, «книга», «человек», «звезда». Собирательные – такие понятия, в которых предметы мыслятся как единое целое. Например, «человечество», «созвездие»,
«космонавтика».
3. Общие понятия делятся на регистрирующие и нерегистрирующие. Регистрирующие – это такие понятия, объем которых составляет конечное множество элементов, в принципе поддающихся учету. Например, «планеты Солнечной системы», «человек», «следователь».
Нерегистрирующие – такие понятия, объем которых составляет бесконечное множество элементов и не поддается принципиальному учету. Например, «число», «атом», «молекула».
Выделяются также понятия с универсальным и нулевым объемами. Класс, состоящий из всех элементов предметной области, называется универсальным классом, или универсумом. Например, класс животных, класс металлов. Класс, который не содержит ни одного элемента, т.е. в объеме которого мыслятся несуществующие предметы,
называется пустым, или нулевым. Например, «вечный двигатель», «русалка».
4. По содержанию понятия делятся на конкретные и абстрактные.
Конкретными называются понятия, в которых мыслятся предметы в совокупности своих признаков («стол», «стул», «человек», «дерево»).
Абстрактными называются понятия, в которых мыслятся свойства или отношения, отвлеченные от самих предметов («счастье», «белизна», «бесконечность»).
5. Понятия бывают положительные и отрицательные. Положительными называются понятия, которые выражают наличие у предмета определенных признаков («красивый», «доблесть», «возможность»).
Отрицательными называются такие понятия, в которых выражается отсутствие признака, зафиксированного в положительном понятии («некрасивый», невозможность», «нехороший»).
Отрицательные понятия образуются от положительных посредством прибавления к положительным понятиям отрицательной частицы «не», приставки «без». Если без отрицательной частицы понятие не употребляется, то оно является положительным (например, «неряха»,«ненастье»).
6. По содержанию понятия делятся на соотносительные и безотносительные. Соотносительные – такие понятия, в которых выражаются предметы, существование одного из которых немыслимо без существования другого («дети» и «родители», «начальник» и «подчиненный», «верх», «низ»).
Безотносительные – такие понятия, в которых отражаются предметы, существование которых не связывается необходимым образом с существованием других предметов («человек», «книга», «парта»).
Определить, к какому виду относится то или иное понятие, – значит дать его логическую характеристику.
III
Рассматривая отношения между понятиями, следует прежде всего различить сравнимые и несравнимые понятия.
Сравнимые – такие понятия, в содержании которых имеются общие признаки, позволяющие эти понятия сравнивать друг с другом. Например, «млекопитающее» и «пресмыкающееся», «стол», «стул», «шкаф» и т. д.
Несравнимые – такие понятия, в содержании которых отсутствуют общие признаки, позволяющие их сравнивать. Например, «квадрат гипотенузы» и «бифштекс», «мнимое число» и «мебель» и т. д.
В логических отношениях могут находиться только сравнимые понятия. Сравнимые понятия делятся на совместимые и несовместимые.
Совместимые понятия – понятия, объемы которых содержат общие элементы. Отношение совместимости представлено следующими видами.
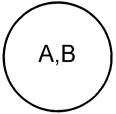
1. Равнозначность (равнообъёмность) имеет место между понятиями, имеющими один и тот же объем, но различное содержание. Например, равнозначными являются понятия «Лев Николаевич Толстой» и «автор романа «Война и мир»»; «человек» и «разумное существо».
Объем понятий в логике принято изображать кругами Эйлера; плоскость круга соответствует логическому классу, а каждая точка – элементу этого класса. Отношение равнозначности графически изображается:
где А, В – символическое обозначение объемов понятий.
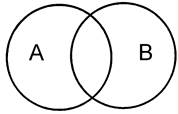
2. Пересечение или частичное совпадение имеет место между понятиями, объемы которых содержат общие элементы. Например, пересекающимися являются понятия «юрист» и «банкир». Графическое изображение пересечения
3. Подчинение (субординация) имеет место между такими понятиями, объем одного из которых полностью входит в объем другого, но его не исчерпывает. Например, в отношении подчинения находятся понятия «высшее учебное заведение» (А) и «университет» (В); «врач» (А) и «врач-терапевт» (В).
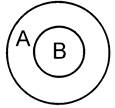
Понятие, объем которого включает объем другого понятия как часть своего объема, называется подчиняющим. Понятие, объем которого входит в объем другого понятия, называется подчиненным.
Несовместимые понятия – понятия, объемы которых не содержат общих элементов.
Виды несовместимости.
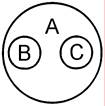
1. Соподчинение (координация) имеет место как минимум между тремя понятиями, одно из которых является родовым, а остальные – видами данного рода, не находящимися в отношении пересечения. Например: «высшее учебное заведение» (А), «институт» (В), «академия» (С).
2. Противоположность (контрарность) имеет место между такими понятиями, одно из которых содержит определенные признаки, а другое эти признаки отрицает, замещая на противоположные. Объемы противоположных понятий не исчерпывает объем родового понятия,между ними существуют промежуточные виды. Например, «черный» (В) и «белый» (С).
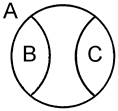
3. Противоречие (контрадикторность) имеет место между понятиями, одно из которых содержит некоторые признаки, а у другого эти признаки отсутствуют, не замещаясь никакими другими. Объемы противоречащих понятий полностью исчерпывают объем родового понятия. Например, «белый» и «небелый».
Символически противоречащие понятия записываются посредством знака отрицания над буквой. 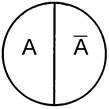
IV
Из двух и более классов с помощью определенных операций можно образовать новый класс. Основными операциями над классами являются объединение классов (сложение), пересечение классов (умножение), образование дополнения к классу (отрицание) и вычитание класса (разность).
При рассмотрении операций над классами вводятся следующие обозначения:
А, В, С… – произвольные классы;
1 – универсальный класс;
0 – пустой класс;
∪ – знак объединения классов (сложения);
∩ – знак пересечения классов (умножения);
А´ (не А) – дополнение к классу А.
Операции над классами иллюстрируются круговыми схемами, универсальный класс обозначается прямоугольником. Объединением классов называется логическая операция, в результате которой образуется новый класс, состоящий из таких объектов, каждый из которых является элементом, по крайней мере, одного из слагаемых классов. Полученный в результате сложения класс А ∪ В называется суммой.
А – класс депутатов Государственной Думы. 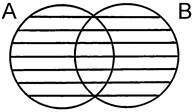
В – класс юристов.
А ∪ В – класс, содержащий всех депутатов Госдумы и всех юристов.
Пересечение классов (умножение) – логическая операция, в результате которой образуется новый класс, состоящий из элементов, являющихся общими для умножаемых классов. Класс А∩В, полученный в результате умножения, называется произведением. 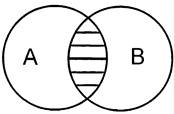
Например, произведением классов «студент» (А) и «шахматист» (В) является новый класс «студент-шахматист».
При умножении множеств, находящихся в отношении несовместимости, получается нулевой класс. Например, умножение классов «гуси» и «утки» дает пустое множество, так как нет таких объектов,которые одновременно были бы и гусями и утками.
Вычитание классов – логическая операция, в результате которой образуется новый класс, состоящий из элементов уменьшаемого класса, не принадлежащих вычитаемому классу.
А-В 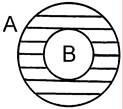
А – класс «химический элемент»
В – класс «металл»
В результате вычитания получается класс, состоящий из химических элементов, не являющихся металлами.
Образование дополнения к классу (отрицание) – логическая операция, состоящая в образовании нового класса, не А (А´), который состоит из элементов универсального класса, не принадлежащих дополняемому классу А. Универсальный класс символически обозначается 1; графически – прямоугольником. 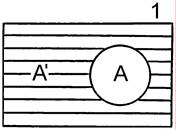
Чтобы образовать дополнение, нужно класс А исключить из универсального класса: 1-А=А´. Например, чтобы образовать дополнение к классу «студент», надо подвергнуть этот класс отрицанию. Полученный класс «не-студент» является дополнением к классу «студент». Класс студентов, сложенный с классом «не-студентов», образует универсальный класс учащихся.
V
Операции над классами подчиняются определенным законам. Обоснование отдельных законов производится с помощью круговых схем; при этом каждому классу на круговой схеме соответствует определенная плоскость. Результат операции, выполняемой в первую очередь, на схемах заштриховывается горизонтальной линией, последующие – вертикальной.
Законы сложения и умножения
1. Закон идемпотентности (подобия) – класс, сложенный сам с собою, или умноженный на себя, равен самому себе.
A ∪ A=A
А ∩ А=А
2. Закон коммутативности – результат сложения и умножения не зависит от того, в каком порядке берутся эти классы.
A ∪ В= В ∪ A
А ∩ В= В ∩ А
3. Закон ассоциативности – результат сложения и умножения более чем двух классов не зависит от порядка выполнения действий.
A ∪ (В ∪ С)= (А ∪ В) ∪ С
А ∩ (В ∩ С)= (А ∩ В) ∩ С.
4а. Закон элиминации (поглощения) для сложения относительно умножения – сумма какого-либо класса и произведения двух классов, одним из сомножителей которого является этот класс, равна этому классу.
A ∪ (А ∩ В) = А = А 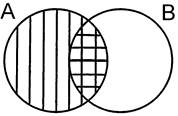
4б. Закон элиминации для умножения относительно сложения – произведение какого-либо класса и суммы двух других классов, одним из слагаемых которой является этот класс, равно умножаемому классу.
А ∩ (А ∪ В) = А. 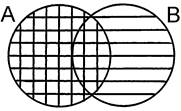
5а. Закон дистрибутивности умножения относительно сложения.
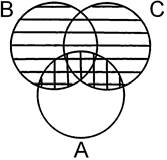
А ∩ (В ∪ С) = (А ∩ В) ∪ (А ∩ С).
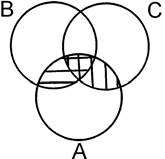 =
= 
5б. Закон дистрибутивности сложения относительно умножения.
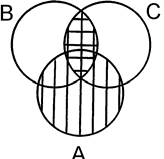
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
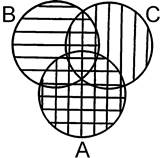 =
= 
Законы дополнения
Законы дополнения вытекают из свойств противоречащих понятий, каковыми являются дополнение и дополняемое понятие.
1. Сумма класса и его дополнения равна универсальному классу А ∪ A' = 1.
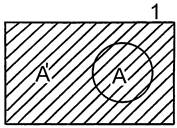
2. Сумма дополняемого класса и универсума равна универсальному классу А ∪ 1=1.
3. Произведение дополняемого класса и универсума равно дополняемому классу А ∩ 1 = А.
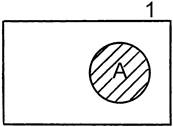
4. Произведение класса и его дополнение является пустым классом А ∩ A' = 0.
5. Дополнением универсума является пустой класс 1' = 0.
6. Дополнением дополнения является дополняемый класс (A') ' = A.
VI
Ограничение и обобщение понятий
В основе перехода от родовых понятий к видовым и от видовых к родовым лежит формально-логический закон обратного отношения между содержанием и объемом понятий.
Ограничение понятий – это логическая операция, посредством которой совершается переход от понятия с большим объемом (род) к понятию с меньшим объемом (вид) посредством прибавления к содержанию родового понятия видообразующего признака. Ограничить понятие – значит перейти от понятия с большим объемом, но меньшим со-
держанием к понятию с меньшим объемом, но большим содержанием. Например, «студент» – «студент-юрист». Пределом ограничения являются единичные понятия. Обобщение понятий – это логическая операция, посредством которой совершается переход от понятия с меньшим объемом (вид) к понятию с большим объемом (род) путем отбрасывания от содержания видового понятия видообразующего признака.
Обобщить понятие – значит перейти от понятия с меньшим объемом, но большим содержанием к понятию с меньшим содержанием, но большим объемом. Например, «студент» – «учащийся». Пределом обобщения понятий являются категории.
Деление понятий
Деление понятий – логическая операция, посредством которой раскрывается объем понятия путем перечисления его видов. Родовое понятие, которое подвергается делению, называется делимым.
Видовые понятия, получающиеся в результате деления, называются членами деления.
Признак, с учетом которого производится установление видов делимого понятия, называется основанием или принципом деления. Различают два вида деления: деление по видоизменению признака и дихотомическое деление.
Деление по видоизменению признака производится таким образом, что все члены деления содержат родовой признак, но в новом качестве. Например, понятие «студент» можно разделить на следующие: «студент дневной формы обучения», «студент вечерней формы обучения», «студент заочной формы обучения». Основанием деления служит форма обучения. Каждое из видовых понятий содержит признаки рода, но в специфическом качестве.
Дихотомическое деление – деление на два взаимоисключающих множества. В процессе дихотомического деления делимое понятие делится на два противоречащих понятия. Например, понятие «человеческое общество» делится на «классовое общество» и «бесклассовое общество»; «преступление» делится на «преднамеренное преступление» и «непреднамеренное преступление» и т. д.
Правила деления
1. Деление должно быть соразмерным, т. е. сумма объемов членов деления должна быть равной объему делимого понятия. Нарушение этого правила приводит к двоякого рода ошибке:
А) неполное деление – имеет место, когда в результате деления указаны не все виды делимого родового понятия. Например, в случае деления понятия «часть речи» на «имя существительное», «имя прилагательное» и «глагол».
Б) деление с излишним членом – имеет место в том случае, когда кроме видов делимого понятия указывают члены деления, не являющиеся видами данного рода. Например, «химические элементы» делятся на «металлы», «неметаллы», «сплавы» (сплавы не являются химическими элементами).
2. Деление должно производиться по одному основанию; логическая ошибка – смешение оснований. Например, «преступления» делятся на «умышленные», «неумышленные» и «должностные».
3. Члены деления должны исключать друг друга, т. е. находиться в отношении несовместимости. Пример логической ошибки на это правило: «параллелограммы делятся на прямоугольники, квадраты и ромбы».
4. Деление должно быть непрерывным, т. е. члены деления должны быть видами одного порядка по отношению к делимому понятию.
Логическая ошибка – скачок в делении. Например, будет допущена ошибка, если сказать: «Сказуемые делятся на простые, составные глагольные и составные именные». Правильным будет сначала разделить сказуемые на простые и составные, а затем составные разделить на составные глагольные и составные именные. Следует отличать логическую операцию деления понятий от расчленения предмета на части. При операции деления содержание делимого понятия всегда можно утверждать относительно каждого члена деления, получая при этом истинные высказывания. В случаях же членения предмета на части получаются бессмысленные высказывания.
Определение понятий
Определение понятий – логическая операция, раскрывающая содержание понятия. Суждение, раскрывающее содержание понятия, называют дефиницией. Понятие, содержание которого раскрывается, называется определяемым (definiendum), или Dfd; понятие, раскрывающее содержание определяемого понятия – определяющим definience),
или Dfn.
Виды определения
Определения делятся на:
1) номинальные и реальные;
2) явные и неявные.
Деление определений на реальные и номинальные зависит от того, что определяется – содержание понятия или значение термина.
Реальное – это определение, посредством которого раскрывается содержание понятия, т. е. определяемый предмет выделяется из класса сходных предметов по специфическим признакам.
Номинальное – определение, посредством которого раскрывается значение вводимого термина.
Явное – определение, в котором выражаются существенные признаки определяемого предмета и имеющие вид Dfd = Dfn.
Неявное – определение, в котором содержание понятия выводится из отношения к другим понятиям. К неявным определениям относятся определения через отношение предмета к своей противоположности, контекстуальные, остенсивные и др.
Наиболее распространенным видом является явное определение через род и видовое отличие и его разновидность – генетическое определение.
Определение через род и видовое отличие состоит из двух понятий – определяемого и определяющего, а сама операция включает в себя два приема:
1) подведение определяемого понятия под более широкое по объему родовое понятие (род);
2) указание видового отличия, т.е. специфического признака, отличающего определяемый предмет от других предметов. Например, в определении «барометр – это метеорологический прибор для измерения величины атмосферного давления» определяемое понятие «барометр» подводится под более общее родовое понятие «метеорологический прибор» и указывается существенный специфический признак
«измерять величину атмосферного давления», посредством которого барометр отделяется от других метеорологических приборов.
Генетическое определение – указывает на происхождение предмета, на способ его образования. Например, «круг – это фигура, образованная вращением отрезка прямой вокруг неподвижного центра». Как разновидность определения через ближайший род и видовое отличие, оно имеет ту же логическую структуру и подчиняется тем же правилам.
Правила определения
1. Определение должно быть соразмерным. Правило соразмерности требует, чтобы объем определяемого понятия был равен объему определяющего, т. е. Dfd = Dfn.
Нарушение этого правила ведет к двоякого рода ошибке: 1) слишком широкое определение, когда объем определяющего понятия шире объема определяемого понятия. Например, «Логика – это наука о мышлении». Здесь не указан специфический признак логики как науки о мышлении, отличающей ее от других наук, изучающих мышление; 2) слишком узкое определение, когда в качестве видового отличия берется отличительный признак не вида, а подвида. Например, «Остров – часть суши, ограниченная со всех сторон морем».
2. Определение не должно заключать в себе круга, что означает, что понятие не должно определяться через самого себя. Ошибка, которая получается вследствие нарушения этого правила, называется порочным кругом. Она встречается в двух разновидностях: круг в определении и тавтология.
Круг в определении означает, что при определении понятия прибегают к другому понятию, которое в свою очередь определяется при помощи первого. Например, «логика – это наука о правильном мышлении, а правильное мышление – это мышление в соответствии с правилами логики». Понятие «логика» определяется через понятие «правильное мышление», а последнее определяется через понятие «логика».
Тавтология – это ошибочное определение, в котором определяемое и определяющее понятия выражены одинаковыми терминами. Например, «Агитатор – человек занимающийся агитацией».
3. Определение должно быть ясным (точным), не допускающим двусмысленности, т. е. должно быть сформулировано в однозначно определенных терминах. Логическая ошибка, связанная с нарушением этого правила – «неясное определение». Например, «Общество есть дополненная или расширенная личность, а личность – сжатое или сосредоточенное общество» (В. Соловьев).
4. Определение не должно содержать художественно-образных средств и оценок. Например, «Артиллерия – бог войны», «Фашизм –отвратительное проявление капитализма».
5. Нельзя определять понятия через такие термины, которые сами нуждаются в определениях. Ошибка подобного рода называется определением неизвестного через неизвестное. Например, «Агностицизм – это разновидность скептицизма».
6. Определение по возможности не должно быть отрицательным. Например, «Роза – не верблюд». Данное определение не указывает на существенный признак, характеризующий предмет и отличающий его от других предметов.
Литература:
1. Арно А., Николь П. Логика, или искусство мыслить. М., 2006.
2. Асмус В.Ф. Учение логики о доказательстве и опровержении.
М., 2005.
3. Войшвилло Е.К. Понятие как форма мышления. М., 2008.
4. Гетманова А.Д. Логика. М., 2006.
5. Ивлев Ю.В. Логика. М., 2007.
6. Кириллов В.И., Старченко А.А. Логика. М., 2008.
7. Логика. Минск, 2006.
8. Свинцов В.И. Логика. М., 2007.
МОСКОВСКИЙ ГУМАНИТАРНО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА ОБЩЕГУМАНИТАРНЫХ И СОЦИАЛЬНО-ЭКНОМИЧЕСКИХ ДИСЦИПЛИН
Тема 4: Логический квадрат. Суждение.
Учебные цели:
Объяснить учащимся основы формирования и генезиса суждения, рассмотреть классификацию простых суждений, объекта и субъекта простого суждения, дать определение понятию «простые суждения», рассмотреть отношения между суждениями по таблице истинности, научить проводить операции с суждениями по логическому квадратудить операць отношения между суждениями по таблице истинности, провести оперждений, дать определение понятию ".
Вопросы:
1.Суждение как форма мышления.
2. Классификация простых суждений.
3. Отношения между суждениями по истинности. Логический квадрат
4. Модальность суждений
5. Сложные суждения и их виды.
6. Выражение одних логических связок посредством других
Автор фондовой лекции:
Преподаватель кафедры ОГ и СЭД,
К.c.н. Тоторкулова М.М.
Рецензенты:
1. Доктор философских наук, профессор Сергодеева Е.А.
2. Доктор социологических наук, профессор Асеев Ю.И.
Лекция обсуждена и одобрена на заседании кафедры Общегуманитарных и социально-экономических дисциплин.
Протокол № от «____» ____________ 20__ г.
Дата добавления: 2016-02-09; просмотров: 822;
