При охвате инерционного интегрирующего звена гибкой ОС
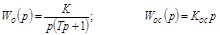
имеем
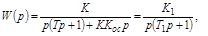
где
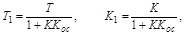
т.е сохраняется то же интегрирующеу звено, но с уменьшеной инерционностью.
Инерционная гибкая ОС.При охвате инерционного интегрирующего звена, т.е:
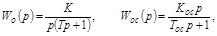
имеем
| |
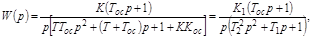
где
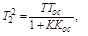
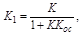
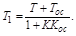
При сохранении интегрирующего свойства звена получается эффект введения производной, т.е интегрирующее звено становится изодромным, и новые 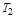 и
и 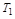 могут быть малыми за счет большого
могут быть малыми за счет большого 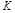 . В последнем случае имеем:
. В последнем случае имеем:
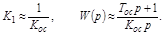
5.4 Корректирующие устройства по внешнему воздействию
Инвариантность [1,c.263-268; 2,c.139-142]
Основной принцип автоматического управления и регулирования состоит в формировании управляющего сигнала по величине ошибки х (с использованием интегралов и производных от х). Если же вводится корректирующее устройство по внешнему воздействию, то получается комбинированное управление – по ошибке и по внешнему воздействию.
Путем введения коррекции по внешнему воздействию удается теоретически свести величину установившейся ошибки к нулю при любой форме внешнего воздействия. Это свойство называется – инвариантностью системы по отношению к внешнему воздействию.
5.4.1 Корректирующее устройство по задающему воздействию
При этом дополнительно к управлению по ошибке х(t) вводится управление по задающему воздействию g(t) через некоторую передаточную функцию 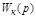 . Структурная схема системы с комбинированным управлением будет выглядеть, как показано на рис. 5.19.
. Структурная схема системы с комбинированным управлением будет выглядеть, как показано на рис. 5.19.
 |
| |
Тогда выходная величина выразится в виде:
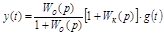 . (5.1)
. (5.1)
Эквивалентная передаточная функция замкнутой системы для регулируемой величины будет равна:
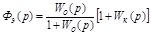 ,
,
а
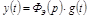 .
.
В случае отсутствия регулирования по задающему воздействию, т.е. при 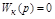 , регулируемая величина связана с g(t) через передаточную функцию замкнутой системы:
, регулируемая величина связана с g(t) через передаточную функцию замкнутой системы:
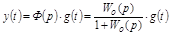 . (5.2)
. (5.2)
Из сопоставления формул (5.1) и (5.2) видно, что введение регулирвоания по задающему воздействию не меняет характеристического уравнения системы, т.к. знаменатели 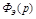 и
и 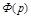 одинаковы. Это означает, что не будет нарушаться не только условия устойчивости, но и сохраняется оценка качества переходного процесса, базирующаяся на использовании корней характеристического уравнения.
одинаковы. Это означает, что не будет нарушаться не только условия устойчивости, но и сохраняется оценка качества переходного процесса, базирующаяся на использовании корней характеристического уравнения.
Эквивалентная передаточная функция по ошибке будет равна:
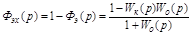 .
.
Отсюда можно найти условие полной инвариантности системы регулирования по задающему воздействию, при котором установившаяся ошибка будет равна нулю при любой форме g(t) ( 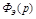 =1, а
=1, а 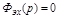 в этом случае):
в этом случае):
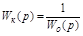 .
.
| |
Структурная схема системы с комбинированным управлением может быть заменена эквивалентной ей обычной схемой САР, работающей по ошибке x(t), с эквивалентной передаточной функцией разомкнутой системы, как показано на рис. 5.20.
 |
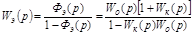 .
.
Рисунок 5.20 – Эквивалентная схема системы с управлением
по задающему воздействию
В некоторых случаях сигнал по задающему воздействию может вводится в некоторую точку внутри канала регулирования (рис. 5.21).
 |
Рисунок 5.21 – Возможный вариант схемы системы
с управлением по задающему воздействию
В этом случае
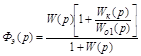 ;
;
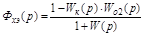 ;
;
| |
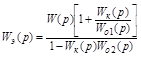 ,
,
где 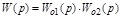 - передаточная функция разомкнутой системы (в случае
- передаточная функция разомкнутой системы (в случае 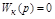 ).
).
Условие полной инвариантности в этом случае:
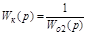 .
.
5.4.2 Корректирующие устройства по возмущению
 |
Пусть задана схема системы с возмущающим воздействием (рис. 5.22).
Рисунок 5.22 – Исходная схема системы с возмущающим воздействием
 |
Введем корректирующее устройство
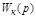 , входом которого является возмущающее воздействие f (рис. 5.23).
, входом которого является возмущающее воздействие f (рис. 5.23).
Рисунок 5.23 – Введение корректирующего устройства
по возмущающему воздействию
Тогда передаточная функция замкнутой системы для регулируемой величины y(t) по f(t) равна:
| |
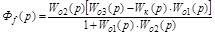 .
.
Условие полной инвариантности по f(t) имеет вид:
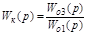 .
.
САР является инвариантной по отношению к возмущающему воздействию, если после завершения переходного процесса, определенного начальными условиями, регулируемая величина и ошибка системы не зависит от этого воздействия.
5.5 Неединичные главные обратные связи
Этот тип корректирующего устройства применяют для уменьшения ошибки, вызванной задающим воздействием в замкнутой системе регулирования.
Введем в главную ОС, которая обычно равна единице, устройство с передаточной функцией 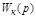 (рис. 5.24). В этом случае на входе системы g(t) сравнивается не непосредственно с выходной величиной y(t), как обычно, а с некоторой величиной z(t).
(рис. 5.24). В этом случае на входе системы g(t) сравнивается не непосредственно с выходной величиной y(t), как обычно, а с некоторой величиной z(t).
 |
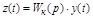 .
.
Рисунок 5.24 – Введение неединичных главных обратных связей
Тогда
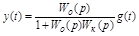 .
.
Эквивалентная передаточная функция замкнутой системы (рис. 5.25):
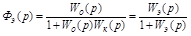 ;
;
| |
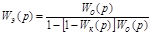 .
.
 |
Рисунок 5.25 – Эквивалентная схема замкнутой системы
с неединичной главной обратной связью
Для полной инвариантности системы требуется 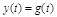 , т.е.
, т.е. 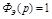 . Отсюда:
. Отсюда:
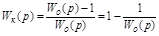 . (5.3)
. (5.3)
Из выражения видно, насколько 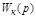 должно отличаться от “обычной” единицы, чтобы система стала инвариантной, т.е. воспроизводила любое g(t) без установившейся ошибки.
должно отличаться от “обычной” единицы, чтобы система стала инвариантной, т.е. воспроизводила любое g(t) без установившейся ошибки.
При этом способе корректировки, как видно из формулы для 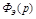 , существенно меняется характеристическое уравнение замкнутой системы. Поэтому нужно следить, чтобы получалось желаемое качество переходного процесса.
, существенно меняется характеристическое уравнение замкнутой системы. Поэтому нужно следить, чтобы получалось желаемое качество переходного процесса.
В статическом режиме (р=0) в системе без астатизма, как видно из равенства (5.3) имеем:
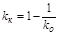 . (5.4)
. (5.4)
Значит, если ввести в главную ОС системы коэффициент усиления 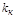 согласно формуле (5.4), то система превращается в астатическую (
согласно формуле (5.4), то система превращается в астатическую ( 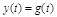 ) без введения интегрирующего звена.
) без введения интегрирующего звена.
| |
Дата добавления: 2016-02-04; просмотров: 907;
