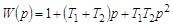ОСНОВНЫЕ ЗАДАЧИ И ПРИНЦИПЫ УПРАВЛЕНИЯ 9 страница
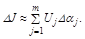
Если известны максимально возможные отклонения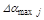 
, то при их независимости друг от друга, используя вероятностные методы, можно найти среднеквадратичный максимум отклонений показателя
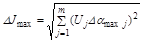
и среднеквадратичный относительный максимум отклонений
.
Если заданы дисперсии отклонений параметров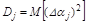 
и они независимы, то можно найти дисперсии показателя качества
.
| |
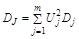5 КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА И МЕТОДЫ ИХ СИНТЕЗА
5.1 Корректирующие устройства и их эквивалентность
[2,c.129-134; 1,c.276-277]
Чтобы добиться желаемого качества процесса управления или регулирования, т.е требуемой точности системы и качества переходного процесса, есть два способа:
- путем изменения параметров данной системы (при этом меняются коэффициенты уравнения и частотные характеристики);
- путем изменения структуры системы, введя дополнительные звенья – корректирующие устройства.
Введение корректирующих устройств позволяет не только улучшить точность системы и качество переходногых процессов, но и сделать систему устойчивой.
Различают четыре основных вида корректирующих устройств:
- последовательные корректирующие устройства;
- параллельные корректирующие устройства;
- корректирующие устройства по внешнему воздействию;
- неединичная главная ОС.
Принятие того или инного типа корректирующих устройств (последовательных, параллельных или ОС) определяется возможностью и удобством их течнического осуществления.
В линейных системах для корректирующего устройства одного типа можно подобрать эквивалентное корректирующие устройство другого типа. Эквивалентность означает,что присоединения к системе регулирования одного или другого корректирующего устройства образует полностью подобные системы. Для получения формул перехода от корректирующего устройства одного типа к другому типу необходимо прировнять результирующие передаточные функции.
при последовательном типе;
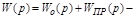при параллельном типе;
в виде ОС(отрицательной).
,
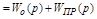
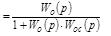где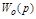 
– передаточная функция заданной части системы.
Отсюда можно получить пять формул перехода от передаточной функции корректирующего звена одного типа к передаточной функции звена другого типа:
| |
,
,
,
,
,
.
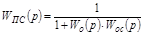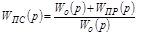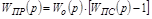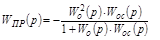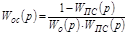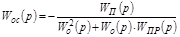Звенья последовательного типа удобно применять тогда, когда в системе регулирования используется электрический сигнал в виде напряжения постоянного тока.
Звенья параллельного типа удобно применять тогда, когда необходимо осуществить сложный закон регулирования с введением производных и интегралов от сигнала ошибки.
Обратные связи отличаются удобством технической реализации.Кроме того,если ОС охватывает участок цепи регулирования,содержащий нелинейность,то влияние этой нелинейности значительно уменьшается.ОС дают значительно лучший эффект в тех случаях, когда из-за воздействия внешних факторов(время, температура и т.п) меняется кoэффициент усиления части цепи регулирования,охватываемой отрицательной ОС.
5.2 Последовательные корректирующие устройства [2,c.129-134]
Последовательные корректирующие устройства (корректирующие фильтры) могут описываться различными передаточными функциями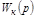 
.
Общая передаточная функция разомкнутой цепи (рис. 5.1) будет:
,
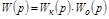а во втором варианте (рис. 5.2)
| |
,
 |
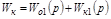где нулями отмечены передаточные функции заданных частей системы.
 |
Рисунок 5.1 – Система с последовательным
корректирующим устройством
Рисунок 5.2 – Один из вариантов цепи с последовательным
корректирующим устройством
Рассмотрим некоторые типовые последовательные корректирующие устройства.
5.2.1 Введение производной от ошибки
Это простейший метод улучшения качества переходного процесса.
 |
Технически осушествляется различными устройствами. Например, дифференциальное звено, в том числе и с инерционностью в виде
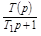(рис. 5.3). Регулирование осуществляется как по ошибке, так и по ее производной.
Рисунок 5.3 – Введение производной от ошибки
Передаточная функция разомкнутой цепи с идеальной производной будет:
.
Заменив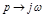 
получим АЧХ и ФЧХ
| |
,
.
 |
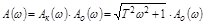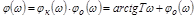При этом существенно, что добавляется положительная фаза. Радиус-вектор АФЧХ поворачивается против часовой стрелки, увеличивая запас устойчивости и улучшая качество переходного процесса (рис. 5.4). Это же видно из ЛАЧХ и ЛФЧХ (рис. 5.5).
 |
Рисунок 5.4 – Изменения АФЧХ при введении
производной от ошибки
Рисунок 5.5 – Изменения ЛАЧХ и ЛФЧХ при введении
производной от ошибки
Введение производной от ошибки может служить стабилизирующим средством, превращая неустойчивую систему в устойчивую. Если бы точка (-1,j 0) лежала бы внутри АФЧХ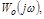 
а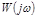 
уже могла бы не охватывать ее.
5.2.2 Увеличение общего коэффициента усиления K
| |
5.2.3 Введение интеграла от ошибки
 |
Введение интеграла от ошибки является методом создания или повышения порядка астатизма системы, а значит и увеличение ее точности (рис. 5.6).
Рисунок 5.6 – Введение интеграла от ошибки
Передаточная функция в этом случае
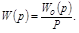
Подставив 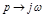получим
 |
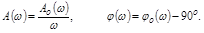
Из-за поворота фазы на
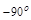ухудшаются условия устойчивости и качество переходного процесса (рис. 5.7 и 5.8). Это может привести и к неустойчивости замкнутой системы, если точка (-1, j 0) окажется внутри АФЧХ 
и не охватывает ее.
Рисунок 5.7 – Изменение АФЧХ при введении интеграла от ошибки
| |
 |
Рисунок 5.8 – Изменения ЛАЧХ и ЛФЧХ при введении
интеграла от ошибки
5.2.4 Изодромное корректирующее устройство
Это корректирующее устройство имеет передаточную функцию вида:
,
 |
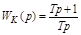объединяя в себе введение интеграла и производной (рис. 5.9). Оно позволяет избежать недостатков предыдущего устройства и получать необходимый порядок астатизма системы, сохраняя устойчивость и качество ее.
Рисунок 5.9 – Введение изодромного корректирующего устройства
ЛАЧХ и ЛФЧХ изодромного устройства имеет вид, показанный на рис. 5.10.
 |
| |
Изменяется низкочастотная часть АЧХ, влияющая на точность системы (повышает ее), а отрицательный сдвиг фазы в части, существенной для условий устойчивости, невелик.
Передаточную функцию изодромного устройства можно представить в виде:
,
 |
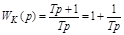т.е. структурно это будет выглядеть так как показано на рис. 5.11.
Рисунок 5.11 – Структурная схема цепи с изодромным
корректирующим устройством
Значит, если при введении интеграла регулирование в системе производится не по величине ошибки х, а только по интегралу от нее, то при изодромном устройстве получается регулирование по ошибке и по интегралу.
5.3 Параллельные корректирующие устройства [2,c.134-139]
В качестве параллельных корректирующих устройств чаще всего используются интегрирующие и дифференцирующие звенья, которые включаются в цепь регулирования параллельно основному сигналу. Эти звенья удобно применять при использовании сложых законов управления, когда наряду с основным сигналом вводятся его производные или интегралы.
Введение интегрирующих звеньев используется для увеличения точности системы в установившихся режимах, т.е снижения установившейся ошибки (рис. 5.12).
 |
Рисунок 5.12 – Введение параллельного интегрирующего
корректирующего устройства
| |
Введение дифференцирующего звена повыша ет запас устойчивости системы (рис. 5.13).
| |
Рисунок 5.13 – Введение параллельного дифференцирующего
корректирующего устройства
Передаточная функция параллельного соединения идеального дифференцирующего звена и основного сигнала
.
|
|
 |
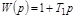Рисунок 5.14 – Введение второй производной от основного сигнала
Введение параллельных интегрирующих звеньев соответствуют поднятию нижних частот (рис. 5.15), а введение параллель6ных дифференцирующих звеньев – поднятию верхних частот (рис. 5.16).
Параллельные корректирующие устройства могут осуществляться в виде дополнительных местных обратных связей (рис. 5.17).
Передаточная функция будет иметь вид:
.
| |
 |
 |
Рисунок 5.15 – ЛАЧХ и ЛФЧХ при введении
параллельного интегрирующего звена
Рисунок 5.16 – ЛАЧХ и ЛФЧХ при введении
параллельного дифференцирующего звена
 |
Рисунок 5.17 – Параллельные корректирующие устройства
в виде местных обратных связей
Основные виды корректирующих местных ОС:
- жесткая ОС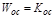 
;
| |
;
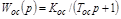- гибкая ОС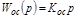 
;
- инерционная гибкая ОС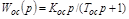 
.
Рассмотрим несколько примеров использования местных ОС в качестве корректирующих устройств.
Положительная жесткая ОС,охватывающая апериодическое звено (инерционное) с 
(рис. 5.18).
Тогда общая передаточная функция:
 |
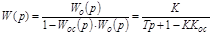
Рисунок 5.18 – Корректирующее устройство в виде
положительной жесткой обратной связи
или
,
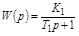где
, 
.
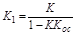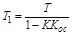Значит положительная жесткая ОС может увеличивать коэффициент усиления, но одновременно увеличивается постоянная времени, т.е. инерционность звена, и при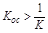 
звено становится неустойчивым.
Отрицательная жесткая ОС,охватывающая апериодическое звено дает общую перелаточную функцию:
,
| |
, 
.
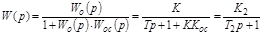Следовательно, жесткая отрицательная ОС уменьшает инерционность звена, улучшая этим качество переходного процесса и может оказать стабилизирующее действие (подобно введению производной), превращая неустойчивую замкнутую систему в устойчивую. Уменьшение коэффициента усиления может быть скомпенсировано за счет других звеньев системы.
При охвате отрицательной жесткой ОС интегрирующего звена, т.е. при 
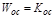, , получим:
,
где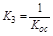 
, 
.
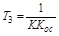Т.е. под действием жесткой обратной связи теряются интегрирующие свойства звена, и оно превращается в инерционное с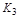 
, определяемым целиком ОС. 
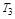будет мала при большом K звена.
Далее будут рассматриваться только отрицательные ОС.
Инерционная жесткая ОС, охватывающая интегрирующее звено.
При этом
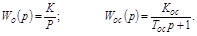
Тогда
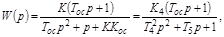
где 
Интегрирующее звено превращается в звено второго порядка с введением производной. 
и интенсивность введения производной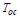 
целиком определяется ОС, и первичный 
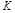влияет на новые постоянные 
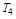и 
, которые будут тем меньше, чем больше 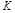. Поэтому при большом 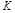охват интегрирующего звена инерционной жесткой ОС эквивалентен усилительному звену с введением производной. При этом
| |
Гибкая ОС.При охвате его колебательного звена, т.е
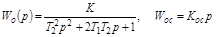
имеем
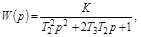
где 
При этом увеличивается демпфирующее свойство колебательного звена ( >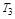 
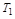), причем не меняется коэффициент усиления 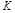. Процесс становится менее колебателеным и может привратится в апериодический (при 
).
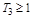Охват апериодического звена гибкой ОС увеличивает только его инерционность.
Дата добавления: 2016-02-04; просмотров: 686;