ОСНОВНЫЕ ЗАДАЧИ И ПРИНЦИПЫ УПРАВЛЕНИЯ 8 страница

Рисунок 4.7 – График вещественной частотной характеристики

Установившееся значение регулируемой величины в о.е. при 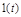на входе равно начальной ординате вещественной частотой характеристики: .

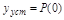Длительность переходного процесса тем меньше, чем больше интервал существенных частот. Имеет место неравенство 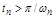, где - интервал положительности .

Если

в интервале до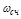

является положительной и невозрастающей, то

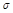в переходном процессе может не быть, а если будет, то не более 18%. В этом случае:

Переходный процесс будет монотонным 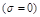, если в интервале имеет отрицательную, убывающую по абсолютному значению производную.

Склонность системы к колебаниям тем больше, чем выше пик 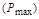у . 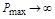, если система находится на колебательной границе устойчивости, что соответствует наличию пары чисто мнимых корней. При нахождении системы на апериодической границе устойчивости, соответствующей наличию одного нулевого корня, значение .

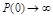4.6.2 Определение запаса устойчивости и быстродействия
по частотным характеристикам

Частотные показатели качества наиболее разработаны в отношении оценки запаса устойчивости, который определяется по удалению 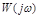АФЧХ разомкнутой системы от точки (-1; j0). Для этого вводятся понятия «запас устойчивости по амплитуде (модулю)» и «запас устойчивости по фазе».

Запас устойчивости по амплитуде определяется точками а и с (рис. 4.8) и соответственно двумя величинами в децибелах:

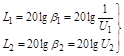Рисунок 4.8 – Определение запаса устойчивости и
быстродействия по АФЧХ разомкнутой системы

Запас устойчивости тем больше, чем больше и . Обычно в устойчивых системах они составляют 6-20 дб. В случае абсолютной устойчивости имеет смысл только величина , а .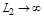

Запасом устойчивости по фазе называется запас по фаз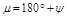е , где 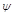- аргумент частотной передаточной функции разомкнутой системы, соответствующий модулю, равному единице (точка в) (рис. 4.8):

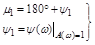В устойчивых системах 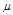составляет около 30-60°.

Иногда вместо дискретных точек, определяющих запас устойчивости системы (точки a, в, c на рис. 4.8) задают запретную область для АФЧХ разомкнутой системы, окружающую точку

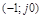. Она может быть построена по заданным значениям запасов устойчивости по фазе

и модулю

(рис. 4.9).

Рисунок 4.9 – Построение запретной области для АФЧХ разомкнутой системы

Недостатком рассмотренного критерия является то, что для определения запаса устойчивости необходимо задать два числа m и b.

Следующей частотной характеристикой является показатель колебательности – максимальное значение

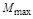АЧХ замкнутой системы, при начальной ординате, равной единице (рис. 4.10):

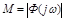Рисунок 4.10 – Определение показателя колебательности
системы по АЧХ замкнутой системы

Чем меньше запас устойчивости, тем больше склонность системы к колебаниям и тем выше резонансный пик. Допускаемое значение 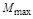для устойчивых систем составляет 1,1-1,5.

Величина 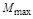может быть определена по виду частотной характеристики разомкнутой цепи данной системы :

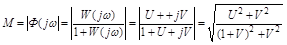Отсюда

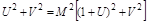
или

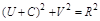где .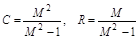

Значит, линии равных значений величины

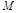, нанесенные на плоскости

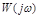, будут окружностями со смещающимся центром влево от начала координат на величину С и меняющимся радиусом R (рис. 4.11).

Рисунок 4.11 – Определение показателя колебательности
системы по виду АЧХ разомкнутой системы

Задаваясь

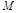от 1 до ¥ можно построить семейство таких окружностей. При

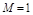окружность вырождается в прямую линию, параллельную оси ординат и проходящую слева от нее на расстоянии 0,5. При

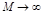окружность вырождается в точку

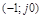При 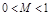получается семейство окружностей справа от линии 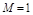и симметрично с первыми. При окружность вырождается в точку начала координат 0.

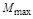Имея такую диаграмму линий , можно по заданной АФЧХ разомкнутой цепи легко определить замкнутой системы и построить всю АЧХ 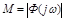замкнутой системы.

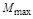определяется по наименьшей окружности 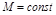, которой коснется АФЧХ. Для кривой 1 на рис. 4.11 это 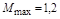. Точки пересечения АФЧХ разомкнутой цепи с окружностями будут определять точки АЧХ с соответствующими значениями ординат, равными .

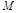Изображенные на рисунке 4.11 характеристики 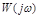1 и 2 соответствуют характеристикам 1 и 2 замкнутой системы 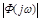(рис. 4.10).

Если необходимо иметь 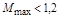, то характеристику 1 нужно скорректировать так, чтобы она не заходила внутрь круга 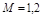. Окружность 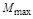является запретной зоной для 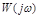. Эта зона окружает точку 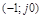и обеспечивает получение заданного запаса устойчивости.

Такие же запретные зоны можно получить и на плоскости ЛАЧХ.

Удобство показателя 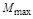в том, что запас устойчивости характеризуется одним числом.

Оценка быстродействия САУ может осуществляться по АЧХ замкнутой системы. Она определяется полосой пропускания, которая находится по частоте , при которой 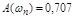(см. рис. 4.10). Чем больше , тем выше быстродействие.

Если переходный процесс заканчивается за 1-2 колебания, то

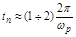где - резонансная частота, при которой .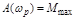

4.7 Определение запаса устойчивости и быстродействия по расположению корней характеристического уравнения [2,c.119-126; 4,c.216-223]

Вид корней характеристического уравнения определяет характер переходного процесса.

Корневыми оценками называются такие, которые основываются на расположении корней характеристического уравнения замкнутой системы, т.е. полюсов Ф(р) замкнутой системы, а также и нулей этой передаточной функции.

Простейшая корневая оценка качества – степень устойчивости h, определяемая расстоянием от мнимой оси (ординат) до ближайшего корня на плоскости корней р характеристического уравнения D(р)=0 замкнутой системы (рис. 4.12).

Если ближайшим является вещественный корень (рис. 4.12, а), то ему соответствует апериодическая составляющая решения для переходного процесса 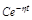(апериодическая степень устойчивости h).

Рисунок 4.12 – Оценка запаса устойчивости по расположению
корней характеристического уравнения

Время ее затухания 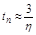характеризует общую длительность переходного процесса, т.е. все члены решения, соответствующие остальным корням, затухают быстрее.

Если ближайший к мнимой оси окажется пара комплексных корней (рис. 4.12, б), то доминирующая составляющая решения для переходного процесса:

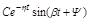
будет колебательной (колебательная степень устойчивости), а оценка 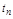остается прежней.

Процесс вычисления h разбивается на два этапа:

1) составление смещенного уравнения,

2) применение критерия устойчивости к смещенному уравнению.

При этом сдвигается мнимая ось влево так, чтобы она прошла через первый, ближайший к ней корень. Для этого в характеристическое уравнение САУ подставляется

и получается смещенное уравнение:

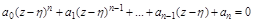. (4.14)

Раскрывая скобки и группируя подобные члены, получим:

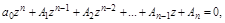(4.15)

где коэффициенты A_i являются функциями h:

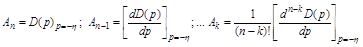Затем к смещенному уравнению (4.15) применяется условие границ устойчивости, например, по Гурвицу: апериодическая - ; колебательная - 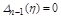, откуда и вычисляется .

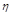Колебательность переходного процесса определяется величиной:

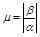где 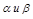-вещественная и мнимая части корней характеристического уравнения.

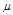характеризует быстроту затухания колебаний за каждый период. Паре комплексных корней 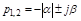соответствует составляющая переходного процесса:

Период колебаний равен: .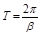

Через один период амплитуда 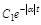уменьшается до величины:

Затуханием за период называют величину: . Тогда

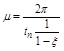Обычно в САУ при .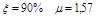

Чем больше величина 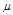, тем слабее затухание колебаний в переходном процессе. Линия образует центральный угол на комплексной плоскости (рис. 4.13).

Рисунок 4.13 – Изображение величины колебательности
на комплексной плоскости

Суммарное требование округленных значени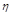й и 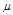приводит к области, изображенной на рис. 4.13, внутри которой должны лежать все корни характеристического уравнения замкнутой системы.

Для определения качества переходного процесса существенны не только корни 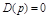, определяемые левой частью дифференциального уравнения системы, но и величины, характеризующиеся правой ее частью. Известно, что :

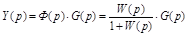где Ф(р) является дробно-рациональной функцией:

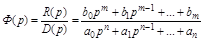Разложив числитель и знаменатель на множители, получим:

Корни числителя

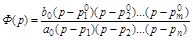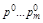называют нулями Ф(р) , т.е. в них она обращается в нуль. Корни знаменателя

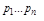являются корнями характеристического уравнения и называются полюсами передаточной функции. В полюсе Ф(р) обращается в бесконечность.

Полюсы характеризуют левую часть, нули - правую часть дифференциального уравнения.

Для уменьшения амплитуд отклонений в переходном процессе желательно, чтобы нули Ф(р) располагались вблизи ее полюсов.

4.8 Интегральные оценки качества

Это такие оценки,которые одним числом оценивают и величины отклонений, и время затухания переходного процесса.

Для монотонного процесса интегральной оценкой может служить площадь под кривой переходного процесса (рис. 4.15):

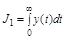Рисунок 4.15 – График монотонного переходного процесса

Процесс тем лучше, чем меньше

. Но для колебательного процесса такая оценка не годится, т.к. нижние площади будут вычитаться из верхних (рис. 4.16).

Рисунок 4.16 – Интегральная оценка колебательного процесса

По минимуму наилучшим оказался бы процесс с незатухающими колебаниями. Поэтому в общем случае принимают квадратичную интегральную оценку качества в виде:

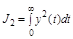Стремление

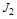к нулю приближает кривую процесса к скачку, при котором уменьшается квадратичная площадь под кривой. Но это вызывает значительное увеличение скорости в начальной части процесса (рывок скорости) (рис. 4.17).

Рисунок 4.17 – График переходного процесса при уменьшении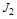

Чтобы получить быстрозатухающий, но достаточно плавный процесс, вводят улучшенную квадратичную интегральную оценку качества:

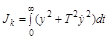где T определяется в соответствии с заданием желаемых свойств переходного процесса и называется постоянной времени.

При стремлении уменьшить оценку 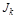кривая переходного процесса приближается к экспоненте с желаемой T. Преобразуем:

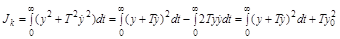Наименьшее возможное значение 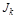будет при:

Решение этого уравнения 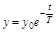и будет экспонентой (пунктирная линия), к которой приближается переходный процесс при стремлении уменьшить 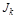(рис. 4.18).

Рисунок 4.18 – График переходного процесса при уменьшении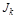

Применяют и другие виды интегральных оценок качества:

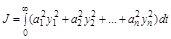где - переменные, характеризующие состояние системы.

Интегральные критерии применяются в теории оптимальных САУ.

4.9 Чувствительность систем регулирования [4,c.241; 1,c.239]

Действительные значения параметров САУ всегда отличаются от расчетных. Это может быть вызвано неточностью изготовления элементов, изменением параметров в процессе эксплуатации, хранения, изменением внешних условий и т.д. Изменение параметров может привести к изменению статических и динамических свойств САУ.

Чувствительностью называется некоторый показатель, характеризующий свойство системы изменять режим работы при отклонении того или иного ее параметра от номинального, или исходного значения. Оценка чувствительности, т.е. оценка влияния на работу САУ отклонения ее параметров от расчетных производится с помощью функций чувствительности. Поскольку качество САУ оценивается с помощью временных или частотных критериев качества, то используются соответственно функции чувствительности временных характеристик и функции чувствительности частотных критериев качества.

Функции чувствительности представляют собой частные производные i-й координаты системы по вариации (изменению) j-го параметра:

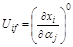или частные производные от используемого критерия качества 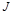по j-ому параметру:

Индекс «0» означает, что частные производные должны приниматься равными значениям, соответствующим номинальным (расчетным) параметрам.

4.9.1 Функции чувствительности временных характеристик

С помощью этой функции оценивают влияние малых отклонений параметров системы от расчетных на временные характеристики системы ( переходную, весовую функции и др.).

Пусть 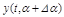- реакция выходной координаты системы на входное воздействие при отклонении параметра a от расчетного значения на величину 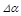. Представим эту реакцию в виде суммы двух слагаемых:

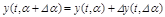, (4.16)

где 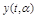- основное движение, соответствующее исходной системе, у которой все параметры равны расчетным значениям и не имеют вариаций;

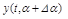- варьированное движение, соответствующее варьированной системе, у которой произошли вариации параметров;

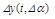- дополнительное движение системы, представляющей разность между варьированным и основным движением.

Разложим 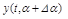в ряд Тейлора по 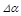относительно :

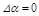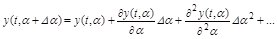(4.17)

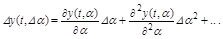
Из сравнения формул (4.16) и (4.17) видно, что дополнительное движение описывается выражением:

которое при малых отклонениях 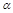от расчетного значения примет вид:

Функция:

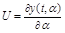
называется функцией чувствительности, с помощью которой можно легко оценить влияние изменения параметра системы на ее дополнительное движение, изменение временных характеристик системы.

Для определения функции чувствительности можно использовать передаточные функции системы. Изображение по Лапласу 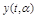имеет вид:

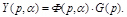
Тогда:

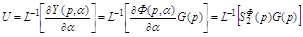, (4.18)

где 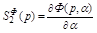- функция чувствительности передаточной функции. Это выражение справедливо лишь в случае, если отклонение 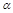от расчетного значения не изменит порядок характеристического уравнения системы. 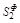характеризует изменение передаточной функции при изменении параметра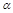

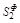От функции

можно перейти к функции чувствительности и с помощью обратного преобразования Лапласа (4.18).

4.9.2 Функции чувствительности частотных критериев качества

В соответствии с критериями качества (показатель колебательности, запас устойчивости по фазе или амплитуде) используют функции чувствительности показателя колебательности, запаса устойчивости по фазе и т.д. С помощью этих функций оценивают чувствительность САУ к изменению параметров.

Если в системе произошли изменения ряда параметров 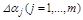, то результирующее изменение некоторого используемого показателя качества:

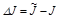где 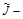варьированное значение показателя, а 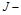исходное значение. Это изменение можно подсчитать по формуле полного дифференциала:

<4 5 6 789 10 >

Дата добавления: 2016-02-04; просмотров: 581;