ОСНОВНЫЕ ЗАДАЧИ И ПРИНЦИПЫ УПРАВЛЕНИЯ 5 страница

Рисунок 2.29 – Представление входного процесса в виде суммы скачков
Сумма 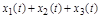 дает искомый процесс
дает искомый процесс
 .
.
Если функция x(t) непрерывна, то ее разбивают на элементарные участки (так называемая решетчатая функция) с шагом 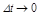 (рис. 2.30).
(рис. 2.30).

Рисунок 2.30 – График решетчатой функции
Кроме единичной ступенчатой функции используют ее производную:
| |

называемую единичной импульсной функцией или дельта-функцией Дирака. Ее определяют равенством:
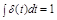
т.е. ее можно трактовать как бесконечно короткий по времени импульс бесконечно большой амплитуды, но с конечной, равной единице, площадью (рис. 2.31).

Рисунок 2.31 – График дельта-функции Дирака
 |
Иными словами, если взять прямоугольник площадью 1 и сжать его по оси t, то прямую бесконечной длины (рис. 2.32).
Рисунок 2.32 – Графическое изображение математического понятия дельта-функции
Если имеется скачок с амплитудой В, то его производная может быть выражена (рис. 2.33):
| |
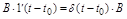 .
.

Рисунок 2.33 – График производной скачка амплитудой В
d-функция позволяет записать график производной в виде суммы d-функций, что позволяет дифференцировать разрывные графики. Так производная ступенчатой функции (2.29) будет описана выражением:

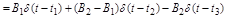 ,
,
а ее график изображен на рис. 2.34.
Воздействия такого типа встречаются в САР в виде кратковременного удара нагрузки (например, при коротком замыкании в электрической сети).

Рисунок 2.34 – График производной ступенчатой функции
2.10.2 Переходные характеристики
| |
Реакция звена (системы) на единичную ступенчатую функцию называется переходной функцией и обозначается h(t-t0) (рис. 2.35).
 |  |
Рисунок 2.35 – Переходная функция
Реакция звена (системы) на импульсную функцию называется импульсной переходной функцией или весовой функцией w(t-t0) (рис. 2.36).
 |  |
Рисунок 2.36 – Импульсная переходная функция
Так как  , то
, то  .
.
Переходная и импульсная переходная функции находятся путем решения дифференциального уравнения звена (системы) при подаче на вход 1(t) или d(t). Доказано, что найти эти характеристики можно более простым путем – по передаточной функции этого звена (системы), используя обратное преобразование Лапласа:

| |
Например:

Таким образом, для определения реакции звена (системы) на единичную или дельта-функции достаточно найти выражение для W(p) и осуществить обратное преобразование Лапласа.
2.11 Определение реакции звена (системы) на входное воздействие с помощью переходных характеристик
Если известны переходные характеристики звена h(t) или w(t) и входной процесс х(t), то можно найти выходной процесс y(t). Суть расчета заключается в том, что входной процесс представляется в виде суммы скачков. Находятся реакции звена (системы) на каждый скачок, а затем, на основании принципа суперпозиции, реакции суммируются. Реакция на скачок величиной D определяется: 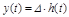 .
.
Упрощение состоит в том, что не решая дифференциального уравнения, реакция системы определяется по известной реакции на скачок .
Если входной процесс непрерывный, то он может быть представлен в виде суммы элементарных скачков через интервал времени  (рис. 2.37).
(рис. 2.37).

Рисунок 2.37 – Представление непрерывного процесса в виде суммы скачков
Так как Dt очень мал, то приращение функции в точке Di равно произведению производной в точке на Dt. Тогда
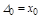 ;
;
| |
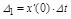 ;
;
 ;
;
а выходной процесс
 .
.
При 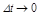 сумма переходит в интеграл, который называется интегралом Дюамеля. А переходный процесс на выходе звена (системы), т.е. реакция, определяется:
сумма переходит в интеграл, который называется интегралом Дюамеля. А переходный процесс на выходе звена (системы), т.е. реакция, определяется:
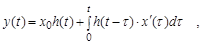
где интегрирование ведется по 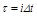 , а t – величина постоянная.
, а t – величина постоянная.
Можно записать это же выражение иначе:
 .
.
Таким образом, не решая дифференциального уравнения, можно получить реакцию системы (звена) на любое воздействие.
3 УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ АВТОМАТИЧЕСКИХ СИСТЕМ
3.1 Понятие устойчивости линейных АСУ
[1,c.107; 2,c.84-90; 3,c.107‑111; 4,c.119-126; 5,c.142-143]
Оценка устойчивости АСУ является центральной задачей при их исследовании. Устойчивость любой физической системы можно определить, как стремление этой системы возвратиться в исходное состояние после того, как она была выведена из него. Например, состояние равновесия шара может быть трех видов (рис. 3.1).

а) устойчивое; б) неустойчивое в) безразличное (нейтральное)
| |
Отклонение системы от установившегося состояния происходит под влиянием внешних воздействий (задающих и возмущающих).
Сформулируем понятие устойчивости, ее условия с математической точки зрения. Пусть АСУ описывается линейным дифференциальным уравнением (2.29).
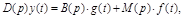 (3.1)
(3.1)
где g(t) и f(t) вызывают отклонение y(t) от ее установившегося значения.
Общее решение неоднородного уравнения (3.1) складывается из частного решения этого уравнения и общего решения соответствующего однородного, которые в ТАУ называются соответственно вынужденной и переходной составляющими
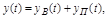 (3.2)
(3.2)
Необходимым и достаточным условием устойчивости линейной АСУ является:
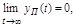
т.е. под устойчивостью линейной системы понимают свойство затухания переходного процесса с течением времени. Например, в системе регулирования напряжения при резком увеличении нагрузки напряжение уменьшится. Но система будет устойчивой, если с течением времени напряжение примет прежнее значение.
Для определения переходной составляющей решим уравнение (3.1) без правой части:
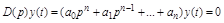 .
.
Решение этого уравнения может быть записано в виде суммы экспоненциальных членов
 (3.3)
(3.3)
где с1,…сn – постоянные интегрирования, а р1,…рn – корни алгебраического уравнения:
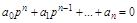 , (3.4)
, (3.4)
называемого характеристическим.
| |
Корни могут быть вещественными (p=a), комплексными p=(a+jb).
Линейная система будет устойчива, если вещественные части всех корней характеристического уравнения будут отрицательными (a<0). Это необходимое и достаточное условие устойчивости системы. Если имеется хотя бы один вещественный корень, или хотя бы одна пара комплексных сопряженных корней с положительной вещественной частью, то вся система становится неустойчивой.
Из (3.3) видно, что  если каждый из ее членов в отдельности при t ® ¥ стремится к 0. Пусть р1 = a1 – один из вещественных корней. Тогда составляющая
если каждый из ее членов в отдельности при t ® ¥ стремится к 0. Пусть р1 = a1 – один из вещественных корней. Тогда составляющая 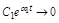 , если
, если  и неограниченно возрастает при
и неограниченно возрастает при  . То же справедливо и для комплексных сопряженных корней
. То же справедливо и для комплексных сопряженных корней 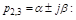
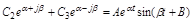 .
.
Эта сумма ®0 при a<0 и неограниченно возрастает при a>0.
Корни характеристического уравнения можно изобразить на комплексной плоскости (рис. 3.2). Для устойчивости системы необходимо и достаточно, чтобы все корни лежали в левой полуплоскости. Мнимая ось (j) представляет собой границу устойчивости.
 |
Рисунок 3.2 – Расположения корней характеристического уравнения
Различают три типа границы устойчивости.
Система находится на апериодической границе устойчивости, если в характеристическом уравнении (3.4) имеется один нулевой корень (на комплексной плоскости он расположен в начале координат), а все остальные корни имеют отрицательные вещественные части (располагаются в левой полуплоскости). Нулевой корень появляется в уравнении (3.4) только при равенстве нулю свободного члена аn=0. Тогда уравнение выглядит:
| |
 .
.
Система устойчива относительно скорости изменения управляемой величины 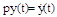 , а не относительно y(t), так как корни характеристического уравнения:
, а не относительно y(t), так как корни характеристического уравнения:
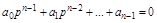
по условию имеют отрицательные вещественные части. Т.е. это нейтрально устойчивая система (см. случай в) с шаром), в котором y(t) может принимать произвольные значения.
Система находится на колебательной границе устойчивости, если в характеристическом уравнении (3.4) имеется одна пара чисто мнимых сопряженных корней, а все остальные корни имеют отрицательные вещественные части. В системе при этом устанавливаются незатухающие гармонические колебания (a=0):
 .
.
Границе устойчивости третьего типа соответствует наличие в характеристическом уравнении (3.4) бесконечного корня. Например, имеем характеристическое уравнение первого порядка:
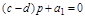 ,
,
корень которого 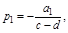 будет отрицательным при с>d (система устойчива) и положительным при c>d (система неустойчива). Значит, границе устойчивости соответствует равенство с=d, при котором корень р1=±¥. Условием границы устойчивости третьего типа является обращение в нуль коэффициента а0 в уравнении (3.4).
будет отрицательным при с>d (система устойчива) и положительным при c>d (система неустойчива). Значит, границе устойчивости соответствует равенство с=d, при котором корень р1=±¥. Условием границы устойчивости третьего типа является обращение в нуль коэффициента а0 в уравнении (3.4).
АСУ, находящиеся на границе устойчивости, неработоспособны, т.к. малейшее изменение параметров системы может привести к неустойчивости.
Все указанные выше условия устойчивости получены в предположении, что система описывается линейным дифференциальным уравнением (3.1), хотя все реальные АСУ не являются строго линейными.
| |
1) Если вещественные части всех корней характеристического уравнения линеаризированной системы отрицательны, то реальная система также устойчива и отброшенные при линеаризации малые нелинейные члены не могут сделать ее неустойчивой.
2) Если имеется хотя бы один корень с вещественной положительной частью, то реальная система неустойчива и отброшенные при линеаризации малые нелинейные члены не могут ее сделать устойчивой.
3) Если линеаризированная система находится на границе устойчивости, то отброшенные при линеаризации малые нелинейные члены могут сделать реальную систему устойчивой или неустойчивой.
Кроме того, линеаризация основана на предположении о малости отклонений входных и выходных звеньев от их установившихся значений. Поэтому приведенные выше условия характеризуют устойчивость системы при малых отклонениях.
Поскольку вычисление корней характеристического уравнения (3.4) оказывается часто затруднительным (особенно при n>3), в ТАУ применяют критерии устойчивости, позволяющие определить знаки вещественных частей без вычисления самих корней.
3.1.1 Необходимые условия устойчивости
Для устойчивости системы необходимо, но не достаточно, чтобы все коэффициенты характеристического уравнения (3.4) были положительными.
Т.е. если все а0, а1,…аn больше нуля, то система может быть устойчивой. Но если хотя бы один из них отрицателен или равен нулю, система неустойчива или неработоспособна, т.к. находится на границе устойчивости.
Представим уравнение (3.4) в виде произведения:
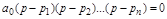 . (3.5)
. (3.5)
При этом будем считать а0>0 (это можно всегда выполнить, если умножить уравнение на –1). В устойчивой системе все корни р1…рn должны быть отрицательными. Если все корни вещественные, т.е. р1=-a1, р2=-a2 и т.д., уравнение (3.5) примет вид:
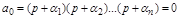 .
.
Если раскрыть скобки, то получим уравнение вида (3.4), все коэффициенты которого положительны, т.к. перемножаются и складываются положительные величины.
| |
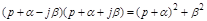
и всегда положительными. Значит и перемножение такого вида множителей дает только положительные коэффициенты характеристического уравнения (3.4).
3.2 Критерий устойчивости Гурвица [1,c.108-138; 2,c.91-95; 3,c.112-140]
Поскольку определение корней характеристического уравнения при большом n делается затруднительным, а положительные коэффициенты этого же уравнения не являются достаточным условием устойчивости систем, то встает задача отыскания критерия устойчивости системы описываемых дифференциальным уравнением любого порядка.
Швейцарским профессором А. Гурвицем в 1895 г. разработан алгоритм решения этой задачи, определяющий последовательность математических операций.
Для характеристического уравнения n-го порядка:
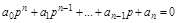
составляют квадратную матрицу (определитель Гурвица) коэффициентов, содержащую n строк и n столбцов:
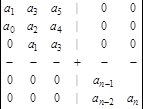 (3.6)
(3.6)
По главной диагонали записываются n коэффициентов, начиная с а1 и кончая аn. Каждый столбец дополняется вверх от диагонали коэффициентами с возрастающими индексами, а вниз – коэффициенты с убывающими индексами. При этом на место коэффициентов с индексами меньше нуля или больше n (отсутствующие коэффициенты) пишутся нули.
| |

 .
.
Определитель Dn включает в себя всю матрицу. Т.к. в последнем столбце матрицы все элементы, кроме нижнего, равны нулю, то этот определитель выражается через предпоследний:
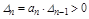 . (3.7)
. (3.7)
Согласно определению в устойчивой системе  должен быть положительным. Поэтому
должен быть положительным. Поэтому 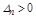 тогда, когда
тогда, когда 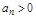 , т.е. свободный член характеристического уравнения должен быть положительным.
, т.е. свободный член характеристического уравнения должен быть положительным.
Границу устойчивости можно получить приравняв  при положительности остальных определителей. Это условие распадается на два (как видно из 3.7):
при положительности остальных определителей. Это условие распадается на два (как видно из 3.7):
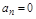 и
и  .
.
Первое условие соответствует апериодической границе устойчивости, второе – колебательной.
Рассмотрим частные случаи критериев устойчивости для систем первого, второго и более высоких порядков.
Уравнение первого порядка а0 р+а1=0;
 ;
;
 .
.
Единственный корень 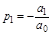 будет отрицательным, если при а0>0 выполняется условие а1>0. Т.е. для системы первого порядка достаточно выполнение необходимого условия устойчивости.
будет отрицательным, если при а0>0 выполняется условие а1>0. Т.е. для системы первого порядка достаточно выполнение необходимого условия устойчивости.
Уравнение второго порядка а0 р2+а1 р+а2=0.
Имеет главный определитель:
 .
.
| |

Третье условие выполняется при положительном а2>0. Т.е. и для системы второго порядка необходимое условие устойчивости является и достаточным. Апериодической границе устойчивости соответствует условие а2=0, а колебательной – а1=0.
Уравнение третьего порядка ао р3+а1 р2+а2 р+а3 = 0.
Имеет главный определитель:
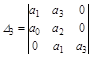
Для этого уравнения имеем четыре условия:
 ;
;
 ;
;
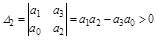 ; (3.8)
; (3.8)
 .
.
Четвертое условие сводится к условию 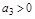 . Условие
. Условие  при
при  ;
; 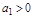 и
и 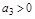 может выполняться только при
может выполняться только при  . Но, кроме того, должно выполняться уравнение четвертого порядка ао р4+а1 р3+а2 р2+а3 р+а4 = 0. Имеет главный определитель:
. Но, кроме того, должно выполняться уравнение четвертого порядка ао р4+а1 р3+а2 р2+а3 р+а4 = 0. Имеет главный определитель:
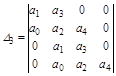 .
.
Условия устойчивости:
 ;
;
 ;
;
 ;
;
| |
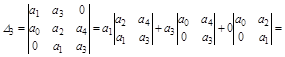
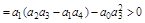 ;
;
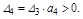
Кроме положительности всех коэффициентов необходимо выполнение условий
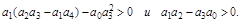
Для уравнения пятого порядка появляются еще дополнительные условия устойчивости, кроме положительности коэффициентов.
Как видно, уже для уравнений выше четвертой степени условия устойчивости по критерию Гурвица получаются громоздкими. Поэтому он используется для анализа уравнений четвертого порядка.
Недостатком алгебраических критериев (в т.ч. и критерия Гурвица) является то, что в случае неустойчивости АСУ они не дают ответа на вопрос, как надо изменить параметры системы, чтобы она стала устойчивой.
3.3 Критерий устойчивости Михайлова
[1,c.139-143; 2,c.95-102; 3,c.141-144; 4,c.131-137; 5,c.149-153]
Сформулирован А.В. Михайловым в 1936 г.
Возьмем характеристический многочлен линейной системы n-го порядка:
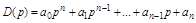 . (3.9)
. (3.9)
Подставим в этот полином чисто мнимое значение р=jw и получим характеристический комплекс:

где вещественная часть 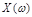 будет содержать четные степени параметра
будет содержать четные степени параметра 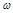 :
:
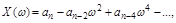 (3.10)
(3.10)
а мнимая часть  - нечетные:
- нечетные:
 (3.11)
(3.11)
| |
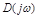 изобразится на комплексной плоскости в виде вектора с проекциями на вещественную и мнимую оси соответственно
изобразится на комплексной плоскости в виде вектора с проекциями на вещественную и мнимую оси соответственно 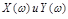 (рис. 3.3).
(рис. 3.3).
 |
Если значения
 менять непрерывно от 0 до
менять непрерывно от 0 до  , то вектор
, то вектор  своим концом опишет кривую (годограф), которая называется кривой Михайлова. Практически кривая Михайлова строится по точкам. Задаются различными значениями
своим концом опишет кривую (годограф), которая называется кривой Михайлова. Практически кривая Михайлова строится по точкам. Задаются различными значениями 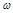 и по (3.10) и (3.11) вычисляются
и по (3.10) и (3.11) вычисляются 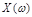 и
и  .
.
Рисунок 3.3 – Изображение кривой Михайлова на
комплексной плоскости
Для устойчивости системы n-го порядка необходимо и достаточно, чтобы вектор 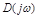 , описывающий кривую Михайлова, при изменении параметра
, описывающий кривую Михайлова, при изменении параметра 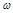 от 0 до
от 0 до  имел угол поворота
имел угол поворота 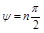 против часовой стрелки.
против часовой стрелки.
Для доказательства представим полином (3.9) в виде произведения сомножителей:
Дата добавления: 2016-02-04; просмотров: 653;
