ОСНОВНЫЕ ЗАДАЧИ И ПРИНЦИПЫ УПРАВЛЕНИЯ 7 страница
-  .
.
Критерием точности служит значение ошибки в установившемся режиме 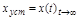 , причем учитывается как ошибка от входного воздействия
, причем учитывается как ошибка от входного воздействия 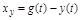 , так и от возмущения
, так и от возмущения 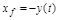 при
при 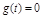 .
.
Критерий запаса устойчивости определяет отдаленность системы от границ устойчивости. Используются два подхода для оценки качества по этому критерию.
Первый основан на рассмотрении переходных процессов (переходных и весовых функций, расположения полюсов и нулей Ф(р) замкнутой системы и т.п.). При этом критериями запаса устойчивости служат величина s и m переходного процесса, его затухание и колебательность.
При втором подходе изучаются частотные характеристики системы, ее резонансные свойства. В качестве критериев запаса устойчивости используют запасы устойчивости по амплитуде и фазе, показатель колебательности и др.
При оценке быстродействия также используются временной и частотный подходы. Критерием быстродействия при временном подходе является время затухания переходного процесса системы tn, а при частотной – полоса пропускания амплитудной характеристики замкнутой системы.
| |
Существует связь между частотами и временными критериями качества процесса управления, которая в общем виде может быть получена только для простых систем второго порядка.
Частотные критерии более эффективные при оценке качества, т.к. вычисления в частотной области проще, чем во временной.
К комплексным критериям качества относятся обобщенные критерии, характеризующие одновременно точность, запас устойчивости и быстродействия. К ним относятся, прежде всего, интегральные оценки свойств кривой переходного процесса.
4.3 Точность при типовых воздействиях [2,c.67-75; 4,c.203-209]
Точность работы САУ в установившихся режимах оценивается по величине установившейся ошибки 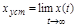 при типовых входных и возмущающих воздействиях. Чем меньше эта ошибка, тем выше качество САУ.
при типовых входных и возмущающих воздействиях. Чем меньше эта ошибка, тем выше качество САУ.
Простейшими типовыми режимами работы являются режимы при постоянной величине внешнего воздействия, при изменении внешнего воздействия с постоянной скоростью, с постоянным ускорением (воздействия в виде квадратичной функции), при гармоническом воздействии.
Величина ошибки может быть определена из общего дифференциального уравнения САУ относительно ошибки (см. п. 2.7).
 , (4.1)
, (4.1)
где D(p), C(p) и 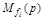 – многочлены; l – число действующих на систему возмущений. В установившемся режиме все производные равны нулю
– многочлены; l – число действующих на систему возмущений. В установившемся режиме все производные равны нулю 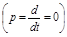 .
.
Преобразуя выражение (4.1) по Лапласу при нулевых начальных условиях, получим изображение ошибки:
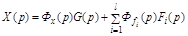 , (4.2)
, (4.2)
где 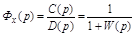 - передаточная функция замкнутой системы по ошибке;
- передаточная функция замкнутой системы по ошибке;
| |
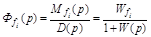 - передаточная функция замкнутой системы по возмущению;
- передаточная функция замкнутой системы по возмущению;
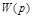 и
и  - передаточные функции разомкнутой системы по управляющему и возмущающему воздействиям.
- передаточные функции разомкнутой системы по управляющему и возмущающему воздействиям.
Исходя из теоремы о конечном значении:
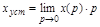 . (4.3)
. (4.3)
Подставив в (4.3) выражение (4.2) получим:
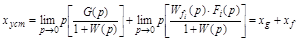 , (4.4)
, (4.4)
где  и
и 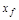 – составляющие установившейся ошибки от воспроизведения входного воздействия
– составляющие установившейся ошибки от воспроизведения входного воздействия 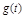 и от действия возмущения
и от действия возмущения  .
.
4.3.1 Постоянное ступенчатое воздействие
При этом 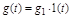 . Для простоты примем одно возмущение
. Для простоты примем одно возмущение 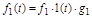 и
и 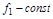 .
.
Установившаяся ошибка при этих воздействиях называется статической 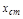 . Изображения воздействий при этом будут
. Изображения воздействий при этом будут
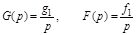 .
.
На основании (4.3) и (4.4) получим:
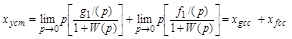 .
.
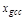 отлична от нуля только в статических системах с
отлична от нуля только в статических системах с 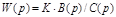 ,
,
где В(р) и С(р) не содержат множителя р, а свободные члены равны 1. Тогда 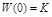 - коэффициенту усиления разомкнутой системы. Тогда
- коэффициенту усиления разомкнутой системы. Тогда
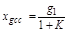 . (4.5)
. (4.5)
| |
 :
:
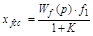 , (4.6)
, (4.6)
где 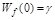 - коэффициент статизма системы с разомкнутой цепью управления, равный отношению
- коэффициент статизма системы с разомкнутой цепью управления, равный отношению 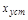 к постоянному возмущению.
к постоянному возмущению.
4.3.2 Воздействие, изменяющиеся с постоянной скоростью
При этом 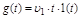 , где
, где 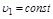 и
и 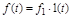 .
.
Такой режим применяется в следящих системах.
В этом случае:
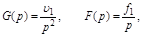
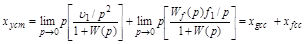 .
.
Второе слагаемое аналогично (4.6) дает статическую ошибку при 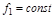 .
.
Первое слагаемое имеет смысл только в случае, когда многочлен С(р), входящий в 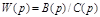 , не имеет свободного члена. Т.е. W(p) должно иметь нулевой корень и может быть представлено в виде:
, не имеет свободного члена. Т.е. W(p) должно иметь нулевой корень и может быть представлено в виде:
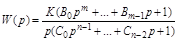 .
.
Тогда первая составляющая установившейся ошибки определяется
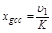 , (4.7)
, (4.7)
и называется скоростной ошибкой.
При постоянном задающем воздействии  в такой системе, обладающей нулевым полюсом в
в такой системе, обладающей нулевым полюсом в 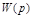 , статическая ошибка
, статическая ошибка 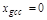 , а имеется постоянное значение скоростной ошибки
, а имеется постоянное значение скоростной ошибки 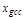 .
.
| |
Как видно из (4.5) и (4.7) для уменьшения величины ошибок нужно добиваться большого значения общего коэффициента К усиления разомкнутой цепи проектируемой системы.
Можно получить САУ с астатизмом второго и более высокого n-го порядка, при условии, что 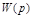 имеет двойной нулевой полюс или нулевой полюс n-го порядка.
имеет двойной нулевой полюс или нулевой полюс n-го порядка.
4.3.3 Воздействие изменяется с постоянным ускорением
При этом 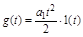 , где
, где  .
.  принимается, как и в предыдущих случаях постоянным. Для такой системы
принимается, как и в предыдущих случаях постоянным. Для такой системы 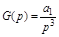 . Первое слагаемое в (4.4) имеет смысл только при астатизме второго порядка, когда:
. Первое слагаемое в (4.4) имеет смысл только при астатизме второго порядка, когда:
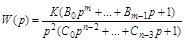 ,
,
и оно называется ошибкой от ускорения:
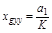 .
.
Аналогично можно говорить и об астатизме системы по отношению к возмущающему воздействию  , но нулевыми полюсами должна обладать
, но нулевыми полюсами должна обладать 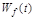 .
.
4.3.4 Гармоническое (синусоидальное) воздействие
При этом  Установившиеся ошибки в этом случае определяются частотными характеристиками замкнутой системы. Рассмотрим ошибку только от действия входного задающего воздействия:
Установившиеся ошибки в этом случае определяются частотными характеристиками замкнутой системы. Рассмотрим ошибку только от действия входного задающего воздействия:
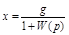 .
.
В линеаризированной системе ошибка в установившемся режиме будет меняться также по гармоническому закону 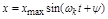 .
.
| |
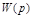 вместо р подставляем
вместо р подставляем  ):
):
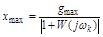 .
.
Так как предполагается, что 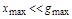 , то модуль знаменателя значительно больше единицы. Поэтому можно записать:
, то модуль знаменателя значительно больше единицы. Поэтому можно записать:
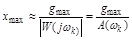 , (4.8)
, (4.8)
где 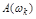 - модуль
- модуль 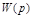 разомкнутой системы при
разомкнутой системы при  . Чтобы вычислить
. Чтобы вычислить 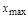 в установившемся режиме нужно знать аналитическое выражение для
в установившемся режиме нужно знать аналитическое выражение для 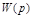 , либо АЧХ или АФЧХ экспериментальной разомкнутой системы.
, либо АЧХ или АФЧХ экспериментальной разомкнутой системы.
Выражение (4.8) позволяет сформулировать требования к ЛАЧХ 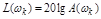 , при которых обеспечивается требуемое значение
, при которых обеспечивается требуемое значение 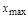 . Для этого необходимо по заданному значению
. Для этого необходимо по заданному значению  и допустимой
и допустимой 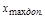 вычислить требуемое значение модуля
вычислить требуемое значение модуля 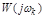 разомкнутой системы в децибелах:
разомкнутой системы в децибелах:
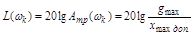 ,
,
 |
отложить его на логарифмической сетке при
 (рис. 4.3).
(рис. 4.3).
Рисунок 4.3 – Определение соответствия ЛАЧХ допустимому значению установившейся ошибки
По полученной контрольной точке  для ЛАЧХ определяют выполнение условия
для ЛАЧХ определяют выполнение условия 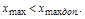 Если ЛАЧХ пройдет ниже точки
Если ЛАЧХ пройдет ниже точки  , то ошибка будет больше допустимой, если выше, то не превосходит допустимой.
, то ошибка будет больше допустимой, если выше, то не превосходит допустимой.
Если использовать основную АЧХ и ФЧХ
| |
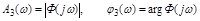
 |

 построенные по главной передаточной функции замкнутой системы, то они включат всю информацию об установившемся слежении за синусоидальным задающим воздействием (рис. 4.4).
построенные по главной передаточной функции замкнутой системы, то они включат всю информацию об установившемся слежении за синусоидальным задающим воздействием (рис. 4.4).
Рисунок 4.4 – Использование ЛАЧХ и ЛФЧХ замкнутой
системы для оценки установившейся ошибки
Установившаяся ошибка воспроизведения  определяется заштрихованными областями ординат. Ошибки в амплитуде при
определяется заштрихованными областями ординат. Ошибки в амплитуде при 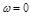 (на рис. 4.4, б) является статической ошибки для системы без астатизма. ФЧХ представляет установившуюся ошибку из-за сдвига фазы на выходе по отношению к
(на рис. 4.4, б) является статической ошибки для системы без астатизма. ФЧХ представляет установившуюся ошибку из-за сдвига фазы на выходе по отношению к 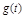 (рис. 4.4, в):
(рис. 4.4, в):
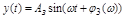 .
.
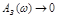 обычно при
обычно при 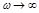 . В результате получается ограниченный диапазон частот
. В результате получается ограниченный диапазон частот  , в котором ошибка воспроизведения амплитуды
, в котором ошибка воспроизведения амплитуды
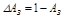
не превышает допустимого значения (рис. 4.4, а). Этот диапазон 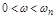 определяет полосу пропускания данной системы, являющуюся важным показателем точности системы. Она характеризует ограничение возможности системы в воспроизведении быстро меняющихся сигналов, что связано с ее инерционностью.
определяет полосу пропускания данной системы, являющуюся важным показателем точности системы. Она характеризует ограничение возможности системы в воспроизведении быстро меняющихся сигналов, что связано с ее инерционностью.
4.4 Точность при медленно произвольно меняющихся воздействиях. Коэффициенты ошибок [2,c.75-79; 4,c.209-211]
Для функции времени 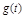 или
или  , имеющей произвольную, но достаточно плавную вдали от начальной точки процесса форму, через некоторое время имеет значение только конечное число
, имеющей произвольную, но достаточно плавную вдали от начальной точки процесса форму, через некоторое время имеет значение только конечное число 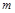 производных, например:
производных, например:
| |
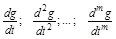 .
.
Изображение ошибки системы от входного задающего воздействия 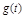 можно определить из (4.2)
можно определить из (4.2)
 .
.
Если разложить 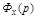 передаточную функцию по ошибке в ряд по возрастающим степеням
передаточную функцию по ошибке в ряд по возрастающим степеням 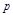 , то
, то
 , (4.9)
, (4.9)
сходящийся при малых значениях 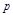 , т.е. больших значениях времени
, т.е. больших значениях времени 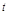 , что соответствует установившемуся процессу изменения
, что соответствует установившемуся процессу изменения  .
.
Перейдя к оригиналу, получим:
 . (4.10)
. (4.10)
Величины  называются коэффициентами ошибок. Они могут быть определены согласно общему правилу разложения передаточной функции
называются коэффициентами ошибок. Они могут быть определены согласно общему правилу разложения передаточной функции 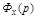 в ряд Тейлора по формулам:
в ряд Тейлора по формулам:
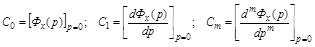 .
.
Так как 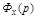 является отношением многочленов
является отношением многочленов 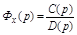 , то эти же коэффициенты ошибок можно получить делением многочлена числителя
, то эти же коэффициенты ошибок можно получить делением многочлена числителя 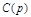 на многочлен знаменателя
на многочлен знаменателя 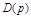 и сравнением получающегося ряда с выражением (4.9). После этого подставив значения коэффициентов в (4.10), получим выражение для
и сравнением получающегося ряда с выражением (4.9). После этого подставив значения коэффициентов в (4.10), получим выражение для 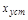 . Коэффициент С0 отличен от нуля только в статических системах. В системах с астатизмом первого порядка С0 = 0; второго порядка - С0 = 0 и С1 = 0, и т.д.
. Коэффициент С0 отличен от нуля только в статических системах. В системах с астатизмом первого порядка С0 = 0; второго порядка - С0 = 0 и С1 = 0, и т.д.
4.5 Определение запаса устойчивости и быстродействия по кривой переходного процесса [4,c.211-213]
Оценку запаса устойчивости и быстродействия можно произвести по виду кривой переходного процесса в САУ при типовом воздействии (входном или возмущающем), например, в виде единичного скачка 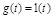 . При этом кривая будет являться переходной характеристикой системы
. При этом кривая будет являться переходной характеристикой системы 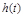 (рис. 4.5).
(рис. 4.5).
| |
 |
Рисунок 4.5 – Оценка запаса устойчивости и быстродействия
по графику переходного процесса
Запас устойчивости может быть охарактеризован перерегулированием
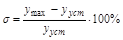 ,
,
допустимая величина которого обычно устанавливается на основании опыта эксплуатации той или иной САУ. В большинстве случаев считается запас устойчивости достаточным, если 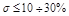 . Но в некоторых случаях требуется полное отсутствие
. Но в некоторых случаях требуется полное отсутствие 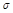 (монотонный переходный процесс), а может допускаться и 50-70%.
(монотонный переходный процесс), а может допускаться и 50-70%.
Быстродействие системы может определяться по длительности переходного процесса 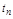 , после которого
, после которого
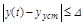 ,
,
где 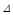 - допустимая ошибка, принимаемая обычно (0,01-0,05)
- допустимая ошибка, принимаемая обычно (0,01-0,05)  .
.
Иногда задается допустимое число колебаний 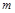 за
за 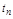 , которое допускается обычно 1-2. Но иногда требуется, чтобы
, которое допускается обычно 1-2. Но иногда требуется, чтобы 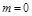 , а может и допускаться до 3-4.
, а может и допускаться до 3-4.
 |
Графически требования к запасу устойчивости и быстродействию сводятся к тому, чтобы
 при
при 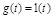 не выходила из области допустимых отклонений управляемой величины
не выходила из области допустимых отклонений управляемой величины  в переходном процессе (рис. 4.6).
в переходном процессе (рис. 4.6).
| |
К сожалению, способов точной оценки перечисленных показателей качества переходного процесса без решения соответствующих дифференциальных уравнений САУ не существует. Поэтому используются приближенные и косвенные методы оценки процессов управления не требующие построения кривой переходного процесса.
4.6 Приближенная оценка качества переходного процесса по частотным характеристикам [2,c.112-119; 4,c.213-216; 223-233]
Прежде чем говорить о частотных оценках, установим связь между частотными характеристиками системы и качеством переходного процесса.
Рассмотрим переходный процесс  при
при 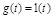 .
.
В изображении по Лапласу
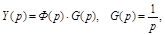
где  - главная передаточная функция замкнутой системы.
- главная передаточная функция замкнутой системы.
Подставив  , запишем выражение для обратного преобразования Фурье (интеграл Фурье):
, запишем выражение для обратного преобразования Фурье (интеграл Фурье):
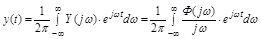 ,
,
где 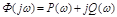 - АФЧХ замкнутой системы, имеющая вещественную
- АФЧХ замкнутой системы, имеющая вещественную  и мнимую
и мнимую 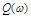 частотные характеристики замкнутой системы.
частотные характеристики замкнутой системы.
Установившиеся значения 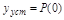 . Тогда
. Тогда
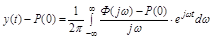 .
.
Заменив 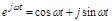 и подставив
и подставив 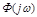 , получим выражение, предварительно отбросив мнимую часть (т.к.
, получим выражение, предварительно отбросив мнимую часть (т.к.  вещественно) его:
вещественно) его:
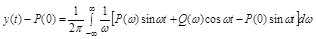 .
.
| |
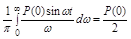 .
.
Тогда получаем:
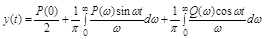 . (4.11)
. (4.11)
Поскольку даны нулевые начальные условия, то нулевые значения функции распространяются и на t<0. Поэтому подставив в (4.11) вместо t величину –t, получим:
 . (4.12)
. (4.12)
Складывая и вычитая (4.11) и (4.12) соответственно получим:
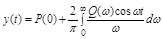 ,
,
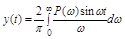 . (4.13)
. (4.13)
Последняя формула (4.13) и используется для частотных оценок качества переходного процесса.
Частотным способом можно определить и весовую (импульсную переходную) функцию замкнутой системы. Если переходной процесс  определен при
определен при 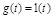 , то
, то 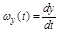 . Дифференцируя (4.13), найдем:
. Дифференцируя (4.13), найдем:
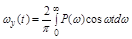 .
.
Существует приближенный способ вычисления по этой формуле. Аналогично находится 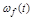 . Зная
. Зная  и
и 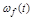 можно определить вынужденную часть процесса управления при любых воздействиях
можно определить вынужденную часть процесса управления при любых воздействиях 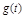 и
и  . Используя интеграл свертки:
. Используя интеграл свертки:
| |
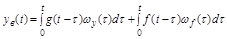 .
.
4.6.1 Приближенная оценка переходного процесса по вещественной частотной характеристике
Эта оценка возможна на основании известной связи (4.13):
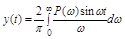 ,
,
где 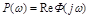 - вещественная частотная характеристика.
- вещественная частотная характеристика.
При этом предполагается, что переходный процесс  вызван скачком входного воздействия
вызван скачком входного воздействия 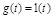 .
.
Анализ выражения (4.13) позволяет судить о переходном процессе по виду вещественной частотной характеристики  . Рассмотрим без доказательств некоторые признаки, по которым можно судить о переходном процессе по
. Рассмотрим без доказательств некоторые признаки, по которым можно судить о переходном процессе по  .
.
 |
Начальная часть
 в основном влияет на конец переходной характеристики, а хвост
в основном влияет на конец переходной характеристики, а хвост  - на начальную часть переходного процесса. При оценке переходного процесса рассматривают интервал существенных частот
- на начальную часть переходного процесса. При оценке переходного процесса рассматривают интервал существенных частот  , выше которого
, выше которого  имеет пренебрежимо малое значение (рис. 4.7).
имеет пренебрежимо малое значение (рис. 4.7).
Дата добавления: 2016-02-04; просмотров: 761;
