ОСНОВНЫЕ ЗАДАЧИ И ПРИНЦИПЫ УПРАВЛЕНИЯ 4 страница
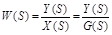 . (2.14)
. (2.14)
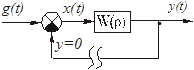
Рисунок 2.20 – Блок-схема при определении основной передаточной фунции
Выражение (2.14) называют основной передаточной функцией разомкнутой системы. Она характеризует динамические свойства передачи сигнала с основного входа на выход АС при разорванной ОС, хотя разомкнутая АС – это уже не АС, а нерегулируемая цепь (УУ-УО).
Если положить g(t) = 0 и разорвать цепь ОС, то получим передаточную функцию разомкнутой системы по возмущению:
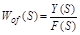 . (2.15)
. (2.15)
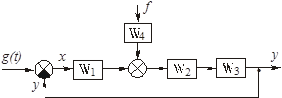
Иногда f(t) действует не на объект, а в любой точке замкнутой цепи (рис. 2.21). Тогда после разрыва главной ОС:
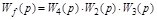 ,
,
 .
.
| |
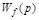 определяет динамические свойства передачи сигнала с возмущающего (не основного) входа на выход АС при разорванной главной ОС.
определяет динамические свойства передачи сигнала с возмущающего (не основного) входа на выход АС при разорванной главной ОС.
Кроме передаточных функций разомкнутой системы есть передаточные функции замкнутой АС.
Основная передаточная функция АС (главный оператор) определяется отношением изображений по Лапласу управляемой величины к задающему воздействию при нулевых начальных условиях и f(t) = 0:
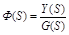 . (2.16)
. (2.16)
Замкнув главную ОС в схеме (рис. 2.20) получим выражение Ф(S) через W(S):
 . (2.17)
. (2.17)
Выражения (2.14) и (2.16) одинаковы по форме, но совершенно различны по содержанию. В (2.14) Y(S) является изображением не управляемой величины, а переменной, снимаемой с того же выхода, что и управляемая y(t). Ф(S) определяет динамические свойства не разомкнутой цепи (как W(S) ), а АС в передаче или обработке основного, задающего сигнала g(t).
Передаточная функция АС по возмущению:
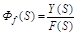 (2.18)
(2.18)
определяется отношением изображений по Лапласу управляемой величины к возмущению при нулевых начальных условиях и при g(t) = 0.
Выразим 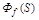 через W(S) и
через W(S) и  . Для этого в структурной схеме (рис. 2.19) сумматор 1 можно убрать (так как g= 0 и x = - y ), а сумматор 2 перенести с выхода на вход звена W(p). Получим структурную схему, показанную на рис. 2.22.
. Для этого в структурной схеме (рис. 2.19) сумматор 1 можно убрать (так как g= 0 и x = - y ), а сумматор 2 перенести с выхода на вход звена W(p). Получим структурную схему, показанную на рис. 2.22.
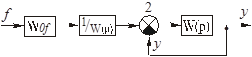
Рисунок 2.22 – Блок-схема при определении передаточной функции замкнутой системы по возмущению
Тогда передаточная функция определяется:
| |
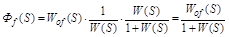 . (2.19)
. (2.19)
Если f (t) приложено в любой точке АС, то:
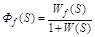 . (2.20)
. (2.20)
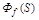 характеризует динамику проникновения возмущений на выход замкнутой АС, или влияние f (t) на y(t) в статическом и динамическом режимах работы АС. Внешнее сходство выражений (2.18) и (2.15) не говорит о сходстве их содержания.
характеризует динамику проникновения возмущений на выход замкнутой АС, или влияние f (t) на y(t) в статическом и динамическом режимах работы АС. Внешнее сходство выражений (2.18) и (2.15) не говорит о сходстве их содержания.
Передаточная функция АС относительно ошибки по задающему воздействию:
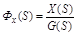 . (2.21)
. (2.21)
определяется отношением изображений по Лапласу ошибка к задающему воздействию при нулевых начальных условиях и при f (t) = 0.
Замкнув ОС в схеме (рис. 2.20) и перенеся узел с выхода на вход звена W(p), получим структурную схему (рис. 2.23), из которой:
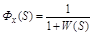 . (2.22)
. (2.22)
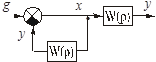
Рисунок 2.23 – Блок-схема при определении передаточной функции замкнутой системы по ошибке
Это выражение можно получить из выражения (2.16), подставив 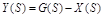 . Тогда
. Тогда 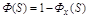 , откуда:
, откуда:
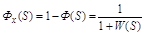 .
.
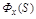 характеризует точность АС в отработке g(t) в статическом и динамическом режимах.
характеризует точность АС в отработке g(t) в статическом и динамическом режимах.
Аналогично можно определить передаточную функцию АС относительно ошибки по возмущению при g(t) = 0 :
| |
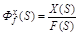 .
.
Если g= 0, то 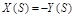 , а
, а
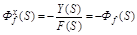 .
.
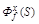 характеризует влияние f (t) на y(t) или точность работы АС при действии на нее возмущения.
характеризует влияние f (t) на y(t) или точность работы АС при действии на нее возмущения.
У передаточных функций (2.17), (2.19), (2.20) и (2.22) знаменатели одинаковы, что является хорошей проверкой правильности вывода этих формул.
Обычно передаточные функции представляют собой рациональную дробь, выраженную отношением двух многочленов от комплексной переменной р . Так передаточная функция УУ (2.11) после ее отыскания примет вид:
 ,
,
где 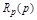 и
и 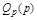 – многочлены (полиномы) относительно р.
– многочлены (полиномы) относительно р.
Так например, если  имеет вид:
имеет вид:
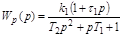 ,
,
то
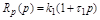 , а
, а 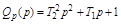 .
.
Передаточные функции УО, выраженные через полиномы от р, примут вид:
по управляющему воздействию
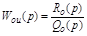
и по любому из возмущений
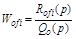 . (2.23)
. (2.23)
Дифференциальное уравнение объекта (2.12), выраженное через полиномы от р, примет вид:
| |
 .
.
Если возмущение приложено в любой точке АС, то:
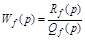 .
.
Передаточная функция разомкнутой системы (2.13) примет вид:
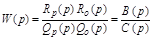 , (2.24)
, (2.24)
где 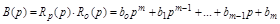 ;
;
 .
.
Коэффициенты полиномов B(p) и С(p) определяются параметрами звеньев АС. Для реальных систем 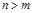 и
и 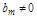 . Если
. Если 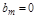 , то:
, то:
 ,
,
т.е. прямая цепь АС реагирует не на ошибку x(t), а на скорость изменения ошибки px(t). Значит в установившемся статическом процессе 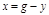 может принимать любые значения, а АС неработоспособна. Условие
может принимать любые значения, а АС неработоспособна. Условие 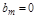 соответствует включению в прямую цепь дифференцирующего звена.
соответствует включению в прямую цепь дифференцирующего звена.
Многочлен С(р) называется характеристическим полиномом, а уравнение
С (р) = 0
характеристическим уравнением разомкнутой системы.
Если свободный член 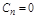 , что соответствует включению в прямую цепь интегрирующего звена, то АС обладает первым порядком астатизма. При двух последовательно включенных в прямую цепь интегрирующих звеньях
, что соответствует включению в прямую цепь интегрирующего звена, то АС обладает первым порядком астатизма. При двух последовательно включенных в прямую цепь интегрирующих звеньях 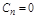 и
и 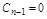 , и АС обладает вторым порядком астатизма. Если
, и АС обладает вторым порядком астатизма. Если 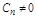 , то АС обладает нулевым порядком астатизма.
, то АС обладает нулевым порядком астатизма.
Зная передаточную функцию (2.24), найдем главный оператор системы (2.17):
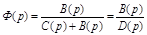 , (2.25)
, (2.25)
| |
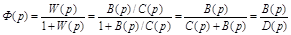 ,
,
где 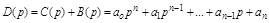 .
.
Многочлен D(p) называется характеристическим полиномом, а
D (p) = 0
или
1 + W (p) = 0
характеристическим уравнением АС.
Так как степень полинома В(p) меньше степени полинома D(p) , т.е. 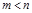 , то Ф(p) – это правильная рациональная дробь, выраженная полиномами.
, то Ф(p) – это правильная рациональная дробь, выраженная полиномами.
По (2.23) и (2.24) найдем передаточную функцию АС по возмущению (2.20):
 , (2.26)
, (2.26)
где 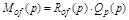 .
.
Чаще всего 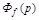 представляет собой правильную рациональную дробь, выраженную полиномами.
представляет собой правильную рациональную дробь, выраженную полиномами.
Передаточная функция АС по ошибке (2.22), выраженная через полиномы от р:
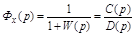 .
.
В 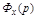 степени полиномов числителя и знаменателя равны, значит
степени полиномов числителя и знаменателя равны, значит 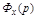 является неправильной рациональной дробью, выраженной полиномами.
является неправильной рациональной дробью, выраженной полиномами.
Зная все передаточные функции АС, можно записать ее дифференциальные уравнения.
На основании (2.16) и (2.25) дифференциальные уравнения АС относительно управляемой величины без учета возмущений:
 (2.27)
(2.27)
или
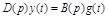 .
.
В соответствии с (2.18) и (2.26) дифференциальное уравнение АС относительно управляемой величины без учета задающего воздействия:
| |
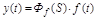 (2.28)
(2.28)
или
 .
.
На основании принципа наложения и выражений (2.27) и (2.28) дифференциальное уравнение АС:
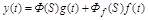
или
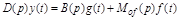 . (2.29)
. (2.29)
Дифференциальное уравнение (2.29) является уравнением движения АС при действии на нее задающего и возмущающего воздействий.
Уравнение движения АС относительно ошибки 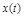 :
:
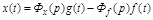 (2.30)
(2.30)
или
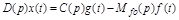 .
.
Ошибка состоит из двух составляющих, вызванных 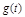 и
и 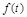 :
:
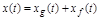
или
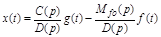 .
.
Уравнение замкнутой системы может быть записано в виде системы уравнений типа:
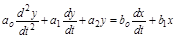 (2.31)
(2.31)
или в стандартном виде символической записи:
| |
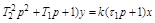 .
.
Эти уравнения обычно второго и первого порядка (но возможно и более высокого порядка). Но уравнение второго порядка всегда можно привести к двум уравнениям первого порядка. Например, положив в (2.31) для простоты 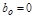 и обозначив
и обозначив
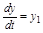 ,
,
получим
 .
.
Представив в аналогичном виде уравнения всех звеньев системы, получим систему уравнений первого порядка, описывающих динамику замкнутой АС:
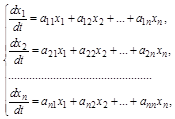 (2.32)
(2.32)
где  - переменные АС, которыми могут быть управляемая величина у и ее производные, ошибка х и ее производные, переменные отдельных звеньев и т.д.
- переменные АС, которыми могут быть управляемая величина у и ее производные, ошибка х и ее производные, переменные отдельных звеньев и т.д.
В правых частях необязательно входят все n переменных, поэтому многие коэффициенты будут равны нулю. В некоторые уравнения справа добавятся задающие 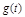 и возмущающие воздействия
и возмущающие воздействия 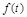 .
.
Запись дифференциальных уравнений вида (2.32) называется нормальной формой или формой Коши.
Характеристическое уравнение этой системы будет иметь вид (  - корни характеристического уравнения):
- корни характеристического уравнения):
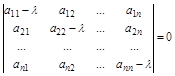 (2.33)
(2.33)
или в развернутом виде:
| |
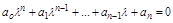 .
.
Система уравнений (2.32) может быть записана в матричной форме:
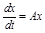 , (2.34)
, (2.34)
а характеристическое уравнение (2.33):
 , (2.35)
, (2.35)
где х – вектор столбец всех переменных (координат состояний системы);
А – матрица коэффициентов;
Е – единичная матрица, т.е.:
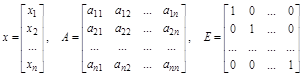 .
.
Краткая запись (2.34) подробно расшифровывается в виде (2.32), а запись (2.35) – в виде (2.33), что соответствует другой краткой записи 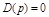 .
.
2.8 Частотные характеристики [1,с.46-53; 2,с.21-25; с.75-82; 4, с.141-143]
Как отмечалось ранее, к линейным системам применим принцип суперпозиции. Входной процесс x(t) можно представить в виде суммы процессов различными способами, одним из которых является представление x(t) (если это периодический процесс), в виде суммы синусоид (разложение в ряд или интеграл Фурье).
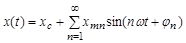 ,
,
где хс – среднее значение;
хmn и j n – амплитуда и фаза соответственно n-ой гармонической составляющей.
Для оценки воздействия входного процесса x(t) на звено достаточно изучить воздействия от каждой синусоиды (гармоники), а потом эти воздействия сложить, используя принцип суперпозиции. Для оценки воздействия установившегося входного процесса в виде гармонического сигнала (синусоиды) на звено используются частотные характеристики звена.
| |
Допустим на вход звена подается процесс в виде синусоиды :
 ,
,
где 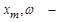 амплитуда и частота синусоиды.
амплитуда и частота синусоиды.
По окончании переходного процесса на выходе звена наступает стационарное (установившееся) состояние. Для линейных систем в стационарном состоянии на выходе устанавливается вынужденный выходной процесс y(t), имеющий ту же частоту w, но другую амплитуду Ym и фазу j (рис. 2.24):
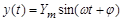 .
.
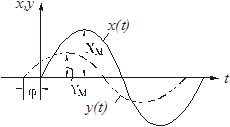
Рисунок 2.24 – Синусоидальный вынужденный выходной процесс
Обозначим через 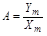 .
.
Если на вход звена подавать синусоиды одинаковой амплитуды 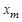 , но разной частоты
, но разной частоты  , то величины А и j будут на выходе звена разными, т.е. они зависят от частоты входного процесса.
, то величины А и j будут на выходе звена разными, т.е. они зависят от частоты входного процесса.
Зависимость 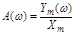 и является амплитудно-частотной характеристикой (АЧХ), которая показывает, как изменяется амплитуда выходного процесса в зависимости от частоты входного.
и является амплитудно-частотной характеристикой (АЧХ), которая показывает, как изменяется амплитуда выходного процесса в зависимости от частоты входного.
Фазочастотной характеристикой (ФЧХ) является зависимость фазы выходного процесса от частоты входного т.е. j(w).
| |
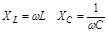 ). Но все эти методы определения АЧХ и ФЧХ громоздки, особенно если система состоит из множества звеньев.
). Но все эти методы определения АЧХ и ФЧХ громоздки, особенно если система состоит из множества звеньев.
Оказывается, что, не решая дифференциального уравнения системы, по ее передаточной функции можно найти частотные характеристики. Для этого необходимо в выражении для W(p) звена или системы заменить p на jw, где  . В результате получается комплексное выражение
. В результате получается комплексное выражение 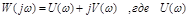 -называют вещественной частотной характеристикой ,
-называют вещественной частотной характеристикой , 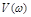 - мнимой. Это же комплексное выражение можно записать в показательной форме:
- мнимой. Это же комплексное выражение можно записать в показательной форме:
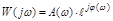
множитель перед 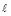 дает АЧХ, а множитель перед j-ФЧХ.
дает АЧХ, а множитель перед j-ФЧХ.
Все выражение W(jw) называется амплитудо-фазочастотной характеристикой (АФЧХ). Графически АФЧХ характеристика может быть построена в прямоугольных координатах (U,V) или изображаться на комплексной плоскости в полярных координатах (A,j), как годограф функции W(jw) (рис. 2.25).

Рисунок 2.25 – Амплитудно-фазочастотная характеристика
Для определения величины вектора А необходимо определить модуль выражения W(jw):
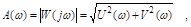
| |
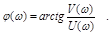
При определении АЧХ можно пользоваться тем условием, что модуль дроби равен отношению модулей числителя и знаменателя. При определении ФЧХ необходимо избавляться от j (мнимых частей) в знаменателе выражения W(jw).
Графики АЧХ и ФЧХ тоже изображаются отдельно графически, причем АЧХ является четной функцией, т.е. 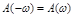 , а ФЧХ – нечетной , т.е.
, а ФЧХ – нечетной , т.е. 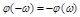 .
.
На практике, в инженерных расчетах чаще применяют логарифмические частотные характеристики. Для построения логарифмической АЧХ (ЛАЧХ) по оси ординат откладывают величину:

измеряющейся в децибелах (рис. 2.26, а). По оси абсцисс откладывается частота w [1/с] в логарифмическом масштабе. Равномерной единицей на оси абсцисс является декада – отрезок, на котором значение w увеличивается в десять раз. Ось абсцисс (Lm=0) соответствует значению А=1, т.е. прохождению сигнала через звено в натуральную величину 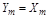 . Верхняя полуплоскость ЛАЧХ соответствует значениям А>1 (усилению амплитуды), а нижняя – значениям А<1 (ослаблению амплитуды). Начало координат обычно помещают в точке w=1 (точка w=0 лежит в -¥), хотя может быть и в другой точке (w=0.1 или w=10 и т.д.).
. Верхняя полуплоскость ЛАЧХ соответствует значениям А>1 (усилению амплитуды), а нижняя – значениям А<1 (ослаблению амплитуды). Начало координат обычно помещают в точке w=1 (точка w=0 лежит в -¥), хотя может быть и в другой точке (w=0.1 или w=10 и т.д.).

Рисунок 2.26 – Логарифмические частотные характеристики
Логарифмическая ФЧХ (ЛФЧХ) имеет ось абсцисс ту же, что и у ЛАЧХ, а по оси ординат отсчет j идет в угловых градусах (рис. 2.26, б).
Частотные характеристики удобны для описания установившихся процессов.
При последовательном соединении звеньев их АЧХ перемножаются (аналогично передаточным функциям), а фазы суммируются.
Частотные характеристики широко используются в электроснабжении при расчете уровней высших гармоник напряжения и тока.
2.9 Воздействие периодических процессов на звено
Предположим, задан периодический входной процесс x(t), поступающий на линейное звено (рис. 2.27).

Рисунок 2.27 – График входного периодического процесса
Т.е. для определения процесса на выходе этого звена можно использовать его частотные характеристики, которые можно определить по передаточной функции (см. п. 2.9).
Процесс x(t) можно разложить в ряд Фурье на гармонические составляющие. Обозначим через 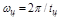 основную частоту; m - номер гармоники; Xmm и ym - амплитуду и фазу гармоники; xc – среднее значение:
основную частоту; m - номер гармоники; Xmm и ym - амплитуду и фазу гармоники; xc – среднее значение:
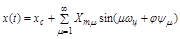 .
.
Чтобы найти все вышеперечисленные величины нужно рассчитать коэффициенты ряда Фурье, определяемые по формулам:
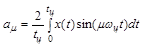 ,
,
| |
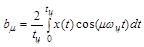 .
.
Тогда:

Амплитудное значение m-ой гармоники на выходе звена определяется как :
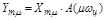 ,
,
а среднее
 .
.
Используя принцип суперпозиции, процесс на выходе звена определяется как:
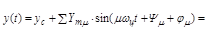
 ,
,
где 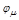 – значение ФЧХ для m-ой гармоники.
– значение ФЧХ для m-ой гармоники.
Таким образом, не решая дифференциального уравнения звена можно получить процесс на выходе звена.
2.10 Переходные характеристики звена
[1,с.65-80; 2,с.20-21; 25-40; 3,с.39-42; 4,с.159-162]
Как уже отмечалось, частотные характеристики позволяют находить решения для стационарного состояния звена или системы. Но в некоторых случаях возникает необходимость исследования работы системы в переходных режимах.
Переходный процесс в САР вызывается приложением задающего или возмущающего воздействия, а также наличием ненулевых начальных условий.
При нахождении кривой переходного процесса в САР имеется трудность, заключающаяся в том, что в реальных САР воздействия носят случайный характер. Поэтому для описания переходных процессов используют некоторые типовые входные воздействия.
2.10.1. Типовые входные воздействия
| |
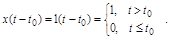
Она определяет собой единичный скачок (единичная функция Хэвисайда) (рис. 2.28).

Рисунок 2.28 – График единичной функции Хэвисайда
Если уровень скачка имеет амплитуду В, то он может быть записан через единичную функцию:
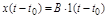 .
.
Воздействие такого типа встречается в САР в виде внезапного скачка задающего или возмущающего воздействия на некоторую постоянную величину (например, внезапное включение или отключение электрической нагрузки в электрических сетях).
С помощью ступенчатой функции можно любой процесс представить как сумму скачков (рис. 2.29):
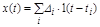 , (2.36)
, (2.36)
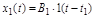 ,
,
 ,
,
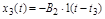 .
.
| |



Дата добавления: 2016-02-04; просмотров: 935;
