ОСНОВНЫЕ ЗАДАЧИ И ПРИНЦИПЫ УПРАВЛЕНИЯ 2 страница

.

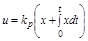Иногда этот закон называют пропорциональным законом с интегральной коррекцией. При этом П-регулирование быстро компенсирует большие по величине возмущения, а И-регулирование осуществляет точную настройку выходной управляемой величины y.

ПИ регуляторы являются астатическими.

1.5.4 Пропорционально-дифференциальный закон (ПД-регулирование)

Алгоритм управления описывается уравнением:

.

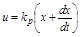При управлении по производной от ошибки вносится опережение в процесс управления, благодаря которому происходит предварение отклонений y от заданного значения.

1.5.5 Пропорционально-интегрально-дифференциальный
закон (ПИД-регулирование)

,

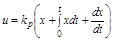при котором регулирование будет астатическим, а производная dx/dt вводится в закон регулирования с целью повышения качества процесса регулирования.

1.5.6 Позиционное регулирование (релейное)

при котором задается верхний и нижний пределы изменения y. Примером такой системы регулирования может служить электронагревательные аппараты с терморегулятором.

1.6 Виды систем автоматического регулирования
[1,с.29-39; 2,с.13-14; 4,с.34-59]

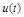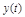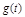АС с замкнутой цепью (с ОС), в которой вырабатывается в результате сравнения действительного значения с называется САР. Автоматическое УУ САР называется автоматическим регулятором.

Сложные АСУ, как правило, состоят из многочисленных замкнутых цепей, т.е. САР, выполняющих отдельные функции регулирования по отдельным параметрам. Например, ракета или самолет имеют несколько САР различных физических величин (скорости, высоты, угловых движений и т.д.), составляющих в целом САР.

По основным видам уравнений динамики процессов управления:

- линейные системы;

- нелинейные системы.

Каждый из этих основных классов делится на:

- системы с постоянными параметрами (уравнения с постоянными коэффициентами);

- системы с переменными параметрами (уравнения с переменными коэффициентами);

- системы с распределенными параметрами (уравнения в частных производных);

- системы с запаздыванием (уравнения с запаздывающим аргументом).

По характеру передачи сигнала:

- непрерывные;

- дискретные (импульсные и цифровые);

- релейные.

По характеру процессов управления:

- детерминированные (определенные параметры и процессы);

- стохастические (случайные параметры и процессы).

По характеру функционирования:

- обычные;

- адаптивные (самонастраивающиеся, саморегулирующиеся, экстремальные);

- терминальные.

Каждый из этих основных классов систем в свою очередь делится по ряду признаков на различные типы и разновидности.

1.6.1 Стабилизирующие, программные, следящие АС

Стабилизирующая – это АС, алгоритм функционирования которой содержит пред­пи­сание поддерживать управляемую величину постоянной при произвольно изменяющихся возмущениях. Задающее воздействие является величиной постоянной:

.

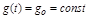Поэтому для этих систем статический режим является наиболее вероятным.

В технике широко используются САР физических величин различных объектов: стабилизация направления, частоты электрической сети, температуры, давления, скорости и т.п.

.

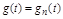Один из примеров систем с программным управлением – система встречного регулирования напряжения в системе электроснабжения, регулирование мощности компенсирующих устройств по времени суток.

Следящая – АС, алгоритм функционирования которой содержит предписание изменять 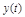в зависимости от неизвестной заранее случайной функции. Задающее воздействие 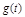изменяется по заранее неизвестному случайному закону:

.

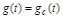Следящие системы применяют для дистанционного управления различными объектами, для телеуправления. При телеуправлении пульт управления отстоит на большое расстояние от УО. В этом случае между задатчиком величины 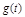и УО вводится радиолиния или другая линия связи. По этому же принципу работают радиолокационные системы сопровождения самолетов, радиокомпас и т.п.

Очевидно, что деление САР на системы стабилизации, программные и следящие условно и зависит в основном от закона изменения задающего воздействия.

1.6.2 Автоматические системы прямого и непрямого регулирования

В АС прямого регулирования отсутствуют устройства, усиливающие по мощности сигналы измерительных или чувствительных элементов. Система прямого регулирования – система, у которой измерительный элемент непосредственно связан с регулирующим органом (ОР).

Мощность ИЭ в такой системе должна быть достаточной для перемещения РО.

Для этого обычно увеличивают вес и габариты ИУ, снижая этим их чувствительность и точность работы. Поэтому для улучшения качества работы ИЭ делают миниатюрными, а слабую мощность их выходных сигналов увеличивают за счет ввода дополнительных устройств в цепь регулирования (например, усилители, двигатели, генераторы и т.п.). Эти устройства или звенья, содержащие источники энергии или использующие для своей работы энергию посторонних источников, называются активными. Мощность выходного сигнала активных звеньев всегда больше мощности входного.

Звенья, не содержащие источников энергии и не использующие для своей работы энергию посторонних источников, называются пассивными (например, системы рычагов, электрические цепи, редукторы и др.). Мощность выходного сигнала пассивных звеньев не больше мощности входного.

1.6.3 Статические и астатические системы регулирования

Если объект и регулятор линейные, то в установившемся процессе значения переменных можно связать уравнениями статики:

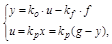
где 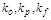– постоянные коэффициенты, называемые соответственно

коэффициентами передачи объекта (по управляющему сигналу и возмущению)

и регулятора.

Подставив из второго уравнения выражение для u в первое, получим:

,

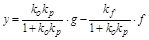т.е. у (регулируемая величина) убывает с ростом возмущения f. Статическая ошибка регулирования:

.

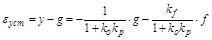Относительную крутизну характеристики:

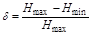
называют статизмом регулирования. Т.е. наибольшая статическая ошибка статического регулятора.

Объекты с жесткой статической характеристикой не нуждаются в автоматическом регулировании. Автоматическое регулирование и сводится к тому, чтобы сделать статическую характеристику объекта жесткой.

Почти все системы прямого регулирования являются статическими.

Когда статическая ошибка недопустима, то переходят к регулированию, в котором установившаяся ошибка при постоянном возмущении равна нулю в силу структуры системы, т.е. астатическому регулированию. АС, в которых отсутствует составляющая статической ошибки по одному из воздействий, называются астатическими.

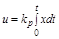, или .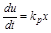

Регулятор будет в равновесии лишь при 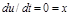, т.е. когда 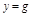. Элементы, реализующие интегральную связь, называются астатическими.

В астатических системах нет позиционной связи между ИЭ и РО.

Позиционная связь сохраняется между значениями выходной величины ИЭ или ошибки х(t) и скоростью изменения управляющего воздействия регулятора .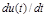

Эта связь линейна, то

,

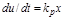откуда

.

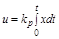Статические характеристики астатических систем абсолютно жесткие, т.е. являются горизонтальными линиями (рис. 1.16).

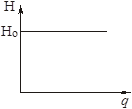
Рисунок 1.16 – Жесткая статическая характеристика астатической АСУ

Однако при высокой статической точности астатических систем качество их динамических свойств низкое. За счет интегральной связи между ИЭ и РО возрастают колебательность и длительность переходного процесса. Поэтому для улучшения статических свойств и неухудшения динамических свойств систем прямого регулирования между ИЭ и РО ставят активное устройство, но с сохранением позиционной связи между ними.

1.6.4 Линейные и нелинейные системы

Все существующие типы уравнений, а значит и АС, можно разделить на линейные и нелинейные.

Линейными называются системы, динамика всех звеньев которых описывается линейными уравнениями (алгебраическими, дифференциальными и др.). Линейные системы делятся на обыкновенные и особые.

Обыкновенными линейными системами называются такие, динамика всех звеньев которых описывается линейными дифференциальными уравнениями с постоянными коэффициентами. Параметры обыкновенных АС постоянны во времени и сосредоточены в пространстве (индуктивность катушки, сопротивление резистора и др.).

К особым относятся такие линейные системы, как:

- АС с переменными параметрами (нестационарные системы), в которых хотя бы одно звено имеет переменные параметры (переменная масса ракеты и др). Описываются они линейными дифференциальными уравнениями с переменными коэффициентами;

- АС с распределенными параметрами, в которых хотя бы одно звено имеет распределенные в пространстве параметры (распределенные индуктивность и емкость линий электропередач). Описываются линейными уравнениями в частных производных;

- АС с запаздыванием, в которых имеется хотя бы одно звено с временной задержкой (трубопроводы, транспортеры, длинные линии передач информации и др.). Описываются линейными уравнениями с запаздывающим аргументом.

АС, содержащие хотя бы одно нелинейное звено, называются нелинейными системами. Нелинейные звенья – это устройства, динамика которых описывается нелинейными уравнениями, в которые входят переменные и их производные не в первой степени, или имеются произведения переменных и их производных, или любые другие нелинейные связи переменных и их производных. Пример – звено с нелинейной статической характеристикой, отражающей связь переменных.

1.6.5 Непрерывные и дискретные АС

Значительным фактором, влияющим на процессы управления или регулирования АС, является характер протекания сигналов во времени. Он может быть непрерывным и дискретным (прерывным).

Сигналы в АС могут быть дискретными из-за того, что задающее или возмущающее воздействие дискретно само по себе или в цепи АС имеется хотя бы одно звено, преобразующее непрерывные сигналы в дискретные. Устройство, осуществляющее такое преобразование, называется звеном прерывистого действия, а процесс преобразования величины в дискретную – квантованием.

Различают квантование по уровню (б) и по времени (в) (рис. 1.17).

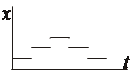
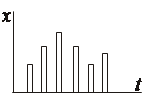
а) б) в)

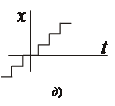
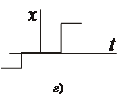
Рисунок 1.17 – Квантование сигнала

Устройство квантования по уровню имеют релейные с зоной нечувствительности (г) или многоступенчатые (д) статичесике характеристики. Все они являются нелинейными.

Устройства, осуществляющие квантование по времени, называются импульсными (рис. 1.18).

Обычно импульсные элементы устроены так, что один из параметров импульсов (h, t_u, T) изменяется в зависимости от значения входной величины. Такое изменение называется модуляцией. Квантование по времени вместе с модуляцией называется импульсной модуляцией. Она является линейной.

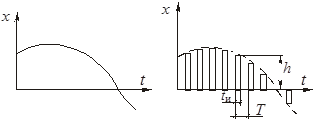
Рисунок 1.18 – Модуляция сигнала

Одновременное квантование сигнала по уровню и по времени осуществляется в цифровых вычислительных машинах. Квантование по уровню связано с тем, что цифровое устройство выдает результат вычисления дискретно, т.е. в виде импульсов через промежутки времени, необходимые для производства вычисления.

2 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕМЕНТОВ И
СИСТЕМ УПРАВЛЕНИЯ

Для аналитического исследования АС необходимо сделать математическое описание отдельных звеньев и всей системы в целом, т.е. выразить существующие связи между переменными и их производными с помощью формул и уравнений. По полученным формулам и уравнениям можно судить о поведении системы, о ее статических и динамических свойствах, в т.ч. и на стадии проектирования.

Математическое описание АСУ и ее элементов часто называют математической моделью.

Прежде чем иметь математическое описание всей системы, необходимо сделать математическое описание каждого звена в отдельности. Из-за сложности физических связей переменных в реальных устройствах (звеньях) обычно прибегают к упрощенному описанию всех звеньев АС. При этом, в зависимости от условий работы устройства, конкретных целей исследования, выбираются необходимые переменные, учитываются наиболее характерные связи между выбранными переменными и их производными и отбрасываются второстепенные.

В большинстве случаев математическим описанием отдельных устройств являются дифференциальные или алгебраические уравнения. Поэтому сделать описание звена означает составить его дифференциальное уравнение.

При поэлементарном описании АС получают уравнения для отдельных входящих в систему элементов и связей, объединяющих эти элементы в систему. В левые части уравнений включают выходные переменные элементов и их производные по времени, в правые части – входные переменные – воздействия на элементы.

Некоторые переменные будут входными для одного элемента и выходными для другого. Число переменных при таком описании оказывается большим, чем число управляемых переменных, т.к. оно включает «промежуточные» переменные (перемещение РО, входные и выходные величины усилителей, преобразователей и т.п.).

Для получения описания системы в целом необходимо исключить все не интересующие исследователя промежуточные переменные и в уравнениях оставить только регулируемые величины и их производные, записываемые в левых частях уравнения, и возмущающие и управляющие воздействия на систему в правых частях.

В общем виде статические линейные системы могут быть описаны алгебраическими уравнениями вида:

,

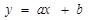которому соответствует прямолинейная статическая характеристика.

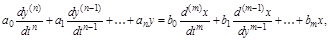
где a_n и b_m – постоянные коэффициенты.

Допустим, что в результате составления уравнения динамики звена получилось линейное дифференциальное уравнение второго порядка:

.

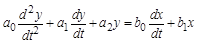В ТАУ принято приводить уравнения звена к стандартному виду в символической записи, введя оператор дифференцирования:

,
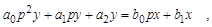
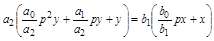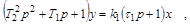(2.1)

где 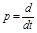– оператор дифференцирования;

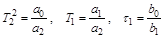- постоянные времени;

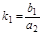- коэффициент усиления звена.

Размерности T₁ и t₁ [с], 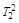[c²], .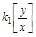

В установившемся состоянии, когда x=const и y=const из (2.1) получим уравнение:

,

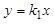соответствующее линейной статической характеристике звена в виде прямой (рис. 2.1), крутизну которой определяет .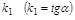

В зависимости от конкретных условий задачи одно и тоже звено может описываться по разному. Например, звено в виде идеальной индуктивности L или емкости С. Входной величиной будем считать подаваемое напряжение U, а выходной –ток, протекающий через звено i. В случае, если напряжение является регулярным воздействием , изменяющимся по синусоиде с постоянной угловой частотой w и действующим значением U. Тогда звено можно рассматривать как статическую систему, а выходная величина I связана с входной U функциональной зависимостью

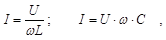
имеющей прямолинейную статическую характеристику.

Если рассматривать то же звено при динамическом процессе, при изменении входной величины U, то уравнения будут другими:

.

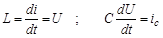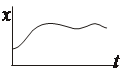
На участке t_и входная величина U меняется, а выходная i остается постоянной, т.е. нет однозначной функциональной связи и зная U нельзя определить значение i (рис. 2.2).

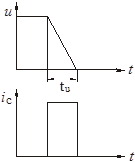
Рисунок 2.2 – Динамические характеристики звена в виде идеальной емкости

В общем случае при составлении уравнения динамики звена или системы они оказываются нелинейными, описывающимися нелинейным дифференциальным уравнением. Например, дифференциальное уравнение второго порядка в общем виде:

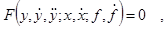
Одним из примеров нелинейного звена может быть электролампа, если рассматривать подаваемое на нее напряжение U как входную, а световой поток Ф- выходную величину, которые будут связаны нелинейным статическим уравнением:

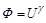при медленных изменениях U. Величина показателя g зависит от типа лампы.

Если уравнения звеньев нелинейные, то их исследование, решение и даже исключение промежуточных переменных, сильно затрудняется. Поэтому при исследовании нелинейных систем их заменяют приближенной линейной моделью, т.е. линеаризируют исходные уравнения, если это возможно.

2.1 Линеаризация уравнений звена [1,с.85; 2,с.16-18; 3,с.29-33; 4,с.61-75]

При линеаризации звена нелинейные связи заменяют приближенными линейными, чтобы облегчить процесс исследования регулирования. Естественно, что всякое упрощение в составлении уравнений и их линеаризацией приводит к описанию, отражающему неполные связи переменных, но оказывающихся практически достаточными.

Линеаризация нелинейного дифференциального уравнения основывается на пред­положении о достаточной малости отклонений всех переменных звена от их установившихся состояний. Это объясняется тем, что замкнутая АС, работающая на принципе отклонений, стремится уменьшить всякие отклонения переменных от требуемых значений.

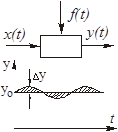
Если переменные x, f, y в статическом режиме характеризуются установившимися значениями: x₀ = const; f₀ = const; y₀ = const, то в динамическом режиме эти переменные можно представить в виде

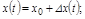
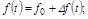
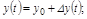
где 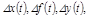обозначены отклонения в процессе регулирования, которые малы (рис. 2.3).

Пусть звено, имеющее входную величину х, выходную – у и возмущающее воздействие – f, описывается нелинейным дифференциальным уравнением 2-го порядка, которое в общем виде записывается:

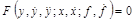. (2.2)

Символом F обозначена нелинейная функция с нелинейными связями переменных:

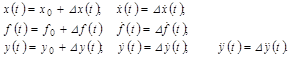
Уравнение установившегося статического состояния звена:

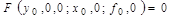. (2.3)

Разложим нелинейную функцию F в ряд Тейлора относительно точки с координатами 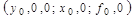. Формула разложения функции 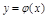в ряд Тейлора в общем виде выглядит:

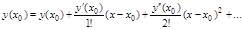
Тогда

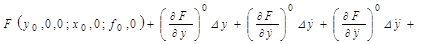
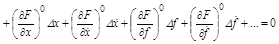, (2.4)

где индекс «0» при частных производных означает, что после взятия производной в ее выражение подставляются установившиеся значения всех переменных: 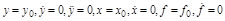. Значит все частные производные в ряде (2.4) представляют собой постоянные коэффициенты. В состав членов высшего порядка малости уравнения (2.4) входят высшие частные производные и квадраты, кубы и более высокие степени отклонений.

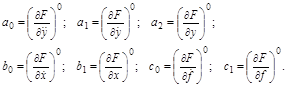
Учтя выражение (2.3), отбросив члены высшего порядка, получим:

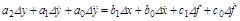. (2.5)

В полученном уравнении (2.5) все переменные и их производные первой степени и произведения переменных. Поэтому оно является линейным (линеаризованным) дифференциальным уравнением с постоянными коэффициентами. А это и было целью линеаризации.

Если дифференциальное уравнение (2.4) равносильно исходному (2.2), но записано в другой форме, то дифференциальное уравнение (2.5) отличается от исходного следующим:

- является приближенным, так как не учтены малые величины высшего порядка;

- описывает динамический процесс лишь в малой окрестности установившихся значений переменных (x₀, y₀, f₀), а не во всей области их изменения;

- является линейным лишь относительно отклонений переменных ( ).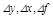

Для представления уравнения (2.5) в символическом виде, принятом в ТАУ , введем оператор дифференцирования 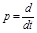. Тогда уравнение (2.5)

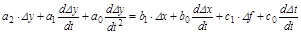
примет вид:

.

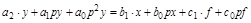Здесь знак D перед переменными с целью удобства опущен. Разделим обе части уравнения на a₂:

.

.

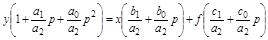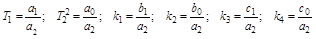Подставив принятые обозначения и выполнив небольшие преобразования, получим символическую запись уравнения:

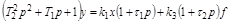, (2.6)

где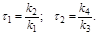

Определим размерность и физический смысл входящих в уравнение величин.

.

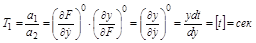Аналогично величины T₂, t₁ и t₂ имеют размерность сек. T₁ и T₂ называются постоянными времени звена и характеризуют его динамические свойства, т.к. проявляются лишь в динамических процессах.

t₁ и t₂ проявляют себя когда входные воздействия x и f изменяются во времени, а значит они также характеризуют динамические свойства звена.