ОСНОВНЫЕ ЗАДАЧИ И ПРИНЦИПЫ УПРАВЛЕНИЯ 6 страница
где 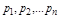 - корни характеристического уравнения.
- корни характеристического уравнения.
Тогда характеристический комплекс примет вид:
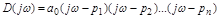 . (3.12)
. (3.12)
Т.е. 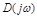 является произведением n комплексных чисел
является произведением n комплексных чисел
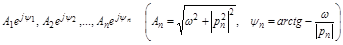 ,
,
| |
 при перемножении складываются. Поэтому результирующий угол поворота вектора
при перемножении складываются. Поэтому результирующий угол поворота вектора 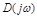 будет равен сумме углов поворота отдельных сомножителей (3.12) при изменении
будет равен сумме углов поворота отдельных сомножителей (3.12) при изменении 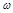 от 0 до
от 0 до 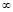 :
:
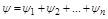 . (3.13)
. (3.13)
Пусть корень вещественный 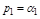 . Тогда аргумент сомножителя
. Тогда аргумент сомножителя 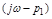 равен
равен 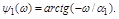 При изменении
При изменении 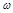 от 0 до
от 0 до 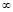 результирующий угол поворота
результирующий угол поворота 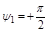 при
при  и
и 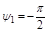 при
при 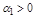 .
.
Пусть два корня 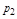 и
и 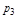 - комплексные сопряженные
- комплексные сопряженные 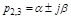 . Тогда аргумент пары сомножителей
. Тогда аргумент пары сомножителей 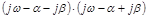 равен
равен
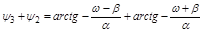 .
.
При изменении 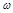 от 0 до
от 0 до 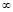 результирующий угол поворота
результирующий угол поворота 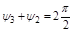 при
при 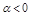 и
и  при
при  .
.
Если характеристическое уравнение будет иметь l корней вещественных или комплексных с положительной вещественной частью, то им будет соответствовать сумма углов поворотов, равная 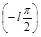 . Остальным (n-l) корням с отрицательной вещественной частью, будет соответствовать сумма углов поворотов, равная
. Остальным (n-l) корням с отрицательной вещественной частью, будет соответствовать сумма углов поворотов, равная 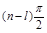 . Общий угол поворота вектора
. Общий угол поворота вектора 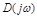 при изменении
при изменении 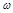 от 0 до
от 0 до 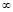 согласно (3.13):
согласно (3.13):
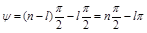 . (3.14)
. (3.14)
Согласно требованию устойчивости необходимо и достаточно, чтобы все корни имели отрицательные вещественные части 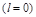 . Поэтому в устойчивой системе на основании (3.14)
. Поэтому в устойчивой системе на основании (3.14) 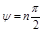 .
.
Для устойчивой системы кривая Михайлова всегда имеет плавную спиралевидную форму, конец которой уходит в  в квадранте, номер которого равен степени n характеристического уравнения (рис. 3.4). Это позволяет сформулировать критерий Михайлова в следующем виде. Для устойчивости автоматической системы необходимо, чтобы кривая Михайлова проходила последовательно столько квадрантов, какова степень n характеристического уравнения, окружая начало координат против хода часовой стрелки.
в квадранте, номер которого равен степени n характеристического уравнения (рис. 3.4). Это позволяет сформулировать критерий Михайлова в следующем виде. Для устойчивости автоматической системы необходимо, чтобы кривая Михайлова проходила последовательно столько квадрантов, какова степень n характеристического уравнения, окружая начало координат против хода часовой стрелки.
| |
 |
Рисунок 3.4 – Виды кривых Михайлова для устойчивых систем n-го порядка
При этом корни уравнений 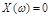 и
и 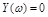 должны чередоваться. Так как кривая Михайлова всегда начинается с точки
должны чередоваться. Так как кривая Михайлова всегда начинается с точки 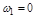 , расположенной на вещественной оси, где мнимая часть обращатся в нуль
, расположенной на вещественной оси, где мнимая часть обращатся в нуль 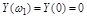 , то при увеличении
, то при увеличении 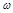 от 0 до
от 0 до 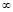 должна обращаться в нуль вещественная часть
должна обращаться в нуль вещественная часть 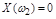 , затем мнимая
, затем мнимая 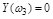 , затем опять вещественная
, затем опять вещественная 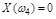 и т.д., причем
и т.д., причем 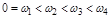 . Поэтому для исследования устойчивости системы достаточно определить ее качественный вид по токам пересечения с осями координат.
. Поэтому для исследования устойчивости системы достаточно определить ее качественный вид по токам пересечения с осями координат.
При четной n кривая 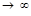 параллельно оси Х, а при нечетной - параллельно оси У ( всегда в n-ом квадранте).
параллельно оси Х, а при нечетной - параллельно оси У ( всегда в n-ом квадранте).
По кривой Михайлова может быть определено наличие границ устойчивости (рис. 3.5).
При апереодической границе устойчивости (нулевом корне) 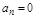 , и кривая Михайлова идет из начала координат (рис. 3.5, а). При колебательной границе устойчивости D(р) обращается в нуль при подстановке
, и кривая Михайлова идет из начала координат (рис. 3.5, а). При колебательной границе устойчивости D(р) обращается в нуль при подстановке 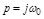 :
:
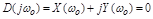 .
.
 |
а) б) в)
| |
системы на границах устойчивости
Отсюда вытекает два равенства :
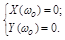 (3.15)
(3.15)
Это значит, что точка 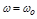 на кривой попадает в начало координат (рис. 3.5, б). При этом
на кривой попадает в начало координат (рис. 3.5, б). При этом 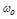 есть частота незатухающих колебаний системы.
есть частота незатухающих колебаний системы.
Для границы устойчивости третьего типа (бесконечный корень) конец кривой перебрасывается в другую сторону. При этом 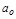 будет проходить через нулевые значения, меняя знак плюс на минус (рис. 3.5, в).
будет проходить через нулевые значения, меняя знак плюс на минус (рис. 3.5, в).
 |
Важно отметить следующее. На границе устойчивости системы все остальные корни характеристического уравнения должны иметь отрицательные вещественные части. Поэтому, кроме условия (3.15), требуется, чтобы кривая проходила бы все остальные квадранты, кроме пропущенного из-за прохождения через начало координат (как показано на рисунках 3.5, а и б). Если же кривая имеет вид, показанный на рис. 3.6, то система находится не на границе устойчивости, а является неустойчивой. Т.е. очертания кривой Михайлова на границе устойчивости должно быть таким, чтобы после малой деформации ее в начале координат (случаи а и б) и при малом
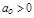 (случай в) можно было удовлетворить критерию устойчивости.
(случай в) можно было удовлетворить критерию устойчивости.
Рисунок 3.6 – Пример кривой Михайлова неустойчивой системы
3.4 Определение границ устойчивости [4,c.137-141]
При расчетах и проектировании АСУ необходимо бывает исследовать влияние ее параметров на устойчивость. Для этого строят область устойчивости, т.е. определяют области значений параметров, при которых система оказывается устойчивой.
| |
Для построения границ устойчивости используются три признака существующих типов границ устойчивости:
апериодической устойчивости 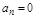 ;
;
третьего типа устойчивости 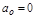 ;
;
для получения условия колебательной границы устойчивости у систем не выше четвертого порядка может применяться критерий Гурвица. При этом  . Для систем более высокого порядка удобнее пользоваться критерием Михайлова, в соответствии с которым
. Для систем более высокого порядка удобнее пользоваться критерием Михайлова, в соответствии с которым 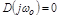 , т.е. прохождение кривой Михайлова через начало координат.
, т.е. прохождение кривой Михайлова через начало координат.
Если интересующие нас два параметра А и В входят линейно в характеристический комплекс, то для границ устойчивости колебательного типа уравнение 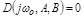 распадается на два:
распадается на два:
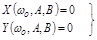 (3.16)
(3.16)
где 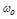 дает значение чисто мнимого корня, т.е. частоту гармонических колебаний системы.
дает значение чисто мнимого корня, т.е. частоту гармонических колебаний системы.
Выражение (3.16) является параметрическим уравнением границы устойчивости при соблюдении дополнительного условия отрицательности вещественных частей всех остальных корней. Это уравнение изображается в виде некоторых кривых на плоскости параметров А и В. Задаваясь разными значениями 
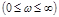 из уравнений (3.16) определяют значения параметров А и В, и по полученным точкам строятся границы устойчивости на плоскости А и В.
из уравнений (3.16) определяют значения параметров А и В, и по полученным точкам строятся границы устойчивости на плоскости А и В.
Для упрощения выделения границ области устойчивости вводится штриховка полученных кривых. При перемещении вдоль кривой в сторону увеличения 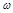 надо штриховать ее с левой стороны, если будет положительным определитель, составленный из частных производных (3.16):
надо штриховать ее с левой стороны, если будет положительным определитель, составленный из частных производных (3.16):
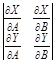 (3.17)
(3.17)
Если определитель (3.17) отрицателен, то кривая штрихуется справа.
| |
3.5 Критерий устойчивости Найквиста [2,c.102-110; 3,c.133-141; 4,c.141-153]
Сформулирован в 1932 г. американским ученым Найквистом. В отличие от критериев Гурвица и Михайлова позволяет судить об устойчивости замкнутой АС по виду АФЧХ разомкнутой системы.
Передаточная функция разомкнутой системы:
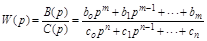 .
.
При подстановке  получим частотную передаточную функцию разомкнутой системы (АФЧХ):
получим частотную передаточную функцию разомкнутой системы (АФЧХ):
 ,
,
где АЧХ 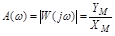 является модулем
является модулем 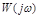 , а сдвиг фаз
, а сдвиг фаз  - ее аргументом (фазой).
- ее аргументом (фазой).
Если изменять  от
от 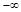 до
до 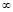 , то вектор
, то вектор 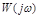 своим концом опишет на комплексной плоскости кривую, которая и называется АФЧХ (рис. 3.7). Ветвь для отрицательных
своим концом опишет на комплексной плоскости кривую, которая и называется АФЧХ (рис. 3.7). Ветвь для отрицательных 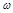 является зеркальным отражением относительно вещественной оси для положительных
является зеркальным отражением относительно вещественной оси для положительных 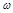 . Поскольку в реальных системах
. Поскольку в реальных системах 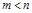 , то при
, то при 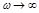 ,
, 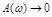 и точка АФЧХ, соответствующая частоте
и точка АФЧХ, соответствующая частоте 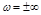 , попадает в начало координат.
, попадает в начало координат.
 |
Рисунок 3.7 – График АФЧХ разомкнутой системы
3.5.1 Общая формулировка критерия Найквиста
| |
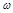 от 0 до
от 0 до 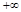 охватывала точку с координатами
охватывала точку с координатами 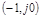 на угол
на угол 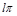 против часовой стрелки, где l – число корней характеристического уравнения разомкнутой системы, имеющих положительные вещественные части. Если АФЧХ проходит через точку
против часовой стрелки, где l – число корней характеристического уравнения разомкнутой системы, имеющих положительные вещественные части. Если АФЧХ проходит через точку 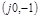 , то замкнутая система находится на колебательной границе устойчивости.
, то замкнутая система находится на колебательной границе устойчивости.
Для доказательства введем вспомогательную функцию:
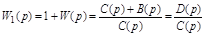 , (3.18)
, (3.18)
где 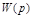 - передаточная функция разомкнутой системы;
- передаточная функция разомкнутой системы;
D(p) и С(р) – соответственно характеристические полиномы замкнутой
и разомкнутой системы.
Найдем комплекс:
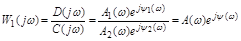
и определим угол поворота (аргумент) вектора  при изменении
при изменении 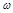 от 0 до
от 0 до 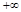 . Этот угол по правилу деления комплексных чисел равен разности аргументов числителя
. Этот угол по правилу деления комплексных чисел равен разности аргументов числителя 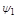 и знаменателя
и знаменателя 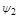 :
:
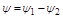 .
.
В п. 3.3 было показано, что в устойчивой замкнутой системе угол поворота вектора 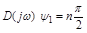 .
.
Если в характеристическом уравнении разомкнутой системы имеется l корней с положительной вещественной частью, а остальные (n – l) корней имеют отрицательные вещественные части, то согласно (3.14):
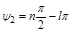 .
.
Отсюда разность углов:
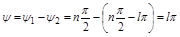 .
.
| |
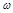 от 0 до
от 0 до 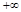 вектор
вектор  должен повернуться вокруг начала координат на угол
должен повернуться вокруг начала координат на угол 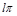 против часовой стрелки. Но
против часовой стрелки. Но  согласно (3.18) отличается от
согласно (3.18) отличается от  на –1. Поэтому в устойчивой замкнутой системе вектор
на –1. Поэтому в устойчивой замкнутой системе вектор 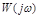 при изменении
при изменении 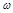 от 0 до
от 0 до 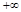 должен повернуться вокруг точки
должен повернуться вокруг точки 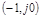 на угол
на угол 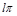 против часовой стрелки. Т.е.
против часовой стрелки. Т.е. 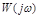 должна охватить точку
должна охватить точку 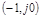 на угол
на угол 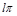 против часовой стрелки, что и требовалось доказать.
против часовой стрелки, что и требовалось доказать.
Если АФЧХ строится для диапазона частот от 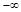 до
до 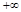 , то угол
, то угол 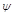 должен быть вдвое больше, т.е.
должен быть вдвое больше, т.е. 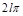 .
.
3.5.2 Частная формулировка Найквиста
В случае устойчивости разомкнутой системы (что чаще всего и бывает) l=0.
Для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой устойчивой системы не охватывала точку 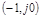 .
.
При l=0 исходя из общей формулировки Найквиста охват точки 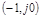 составит угол
составит угол 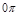 , что фактически означает неохват ее.
, что фактически означает неохват ее.
3.6 Использование логарифмических частотных характеристик для
оценки устойчивости [2,c.108; 4,c.150]
Для устойчивости замкнутой системы необходимо и достаточно, чтобы ЛФЧХ устойчивой разомкнутой системы не пересекала ось частот (1) или пересекало бы ее четное число раз при ЛАЧХ 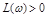 (рис. 3.8 и 3.9).
(рис. 3.8 и 3.9).
Колебательной границе устойчивости соответствует случай, когда ЛАЧХ ЛФЧХ пересекают ось частот в одной точке (3).
 |
Рисунок 3.8 – Определение устойчивости системы по АФЧХ
1 – абсолютно устойчивая система;
2 – неустойчивая система;
| |
 |
Рисунок 3.9 – Определение устойчивости системы по АФЧХ
1 – абсолютно устойчивая система.
4 ОЦЕНКА КАЧЕСТВА ПРОЦЕССОВ УПРАВЛЕНИЯ
4.1 Требования к качеству процесса управления. Показатели качества
[2,c.111-112; 4,c.25-28; 200-203]
Устойчивость АСУ обеспечивает затухание переходных процессов с течением времени, т.е. обеспечивается возможность прихода системы в установившееся состояние при любом внешнем воздействии.
Но, кроме этого требуется, чтобы установившееся состояние было близко к заданному и, чтобы затухание переходного процесса было достаточно быстрым, а отклонения (колебания) при этом были бы невелики.
Поэтому после обеспечения устойчивости системы необходимо обеспечить требуемое качество процесса управления, в понятие которого входят:
- качество переходного процесса;
- точность системы в установившемся состоянии.
Показатели качества переходного процесса чаще всего определяются по реакции АС на ступенчатое изменение входного воздействия (рис. 4.1).
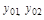 и
и 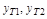 - установившиеся и требуемые значения управляемой величины до и после момента
- установившиеся и требуемые значения управляемой величины до и после момента 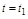 изменения входного воздействия.
изменения входного воздействия.
К показателям качества переходного процесса (динамическим показателем качества АС) относятся:
- динамическая ошибка 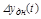 - разность между требуемым и действительным значением управляемой величины, возникающая в процессе управления (показана на рисунке штриховкой)
- разность между требуемым и действительным значением управляемой величины, возникающая в процессе управления (показана на рисунке штриховкой)
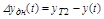 ,
,
| |
 |
Рисунок 4.1 – Определение показателей качества по графику переходного процесса
которая характеризует точность работы АС в динамическом режиме;
- перерегулирование (максимальное отклонение управляемой величины 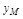 )
)
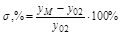 .
.
Теоретически 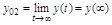 . Но в реальных АС из-за потерь переходные процессы затухают за небольшое конечное время;
. Но в реальных АС из-за потерь переходные процессы затухают за небольшое конечное время;
- время переходного процесса 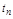 определяемое длительностью переходного процесса от момента приложения воздействия
определяемое длительностью переходного процесса от момента приложения воздействия 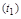 до момента, после которого имеет место неравенство
до момента, после которого имеет место неравенство
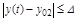 ,
,
где 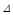 - заданная постоянная величина (1¸5% от
- заданная постоянная величина (1¸5% от 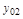 ).
). 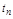 характеризует степень быстродействия АС.
характеризует степень быстродействия АС.
| |
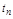 . Оно характеризует меру колебательности АС.
. Оно характеризует меру колебательности АС.
 |
Чем меньше числовые значения показателей качества переходного процесса, тем лучше динамические свойства АС. Все эти показатели взаимосвязаны, и изменение одного из них ведет к изменению других. Поэтому достижение одновременного минимума всех показателей – задача очень трудная. При проектировании АС важно, чтобы они не выходили за определенные границы (рис. 4.2).
Рисунок 4.2 – График допустимых границ изменения показателей качества
Точность системы характеризуется такими показателями, как: статические и скоростные ошибки, возникающие при различных типовых воздействиях; коэффициенты ошибок при произвольном внешнем воздействии и др.
Для оценки точности (статических свойств) АС используют так называемые статические ошибки по задающему и возмущающим воздействиям. Статической ошибкой 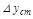 называется отклонение управляемой величины y(t) от требуемого значения yT в статическом режиме, т.е. при постоянных значениях входных воздействий.
называется отклонение управляемой величины y(t) от требуемого значения yT в статическом режиме, т.е. при постоянных значениях входных воздействий.
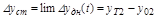
В общем виде статическая ошибка АС:
 ,
,
где 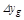 и
и 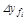 – составляющие от постоянных
– составляющие от постоянных 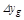 и
и 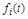 . Чем меньше статическая ошибка, тем выше точность и статические свойства АС.
. Чем меньше статическая ошибка, тем выше точность и статические свойства АС.
4.2 Критерии качества [4,c.200-203]
Любая АСУ должна управлять объектом или процессом с определенной точностью. В конечном счете качество управления зависит от мгновенных величин ошибки, равных разности
| |
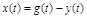
между заданным g(t) и фактическим y(t) значениями регулируемой величины. Ошибка определяется характером изменения g(t) и y(t), которые изменяются чаще всего случайным образом. Поэтому оценка качества управления по мгновенным значениям ошибкам x(t) не используется, а применяются вероятностные оценки ошибки.
В ТАУ применяют также методы, позволяющие оценивать качество систем по их поведению в типовых режимах, когда случайные воздействия апроксимируются заданными (типовыми) функциями времени. Оценка качества САУ ведется по критериям качества, которые можно разделить на :
- критерии точности;
- критерии запаса устойчивости;
- критерии быстродействия;
- комплексные критерии.
Критерии точности используют для оценки величин ошибок, возникающих в различных типовых установившихся режимах, а также при плавном, медленном изменении g(t) и f(t). К типовым режимам относятся такие, при которых:
- 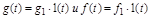 , где
, где 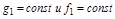 ;
;
- 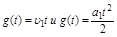 при
при 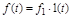 , где
, где 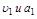 - скорость и ускорение изменения входного воздействия;
- скорость и ускорение изменения входного воздействия;
Дата добавления: 2016-02-04; просмотров: 639;
