ОСНОВНЫЕ ЗАДАЧИ И ПРИНЦИПЫ УПРАВЛЕНИЯ 3 страница
В установившемся процессе, когда все производные равны нулю (в уравнении (2.6) р=0), получим уравнение статического режима:
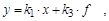
являющееся линеаризированной статической характеристикой звена в малых отклонениях.
Коэффициент 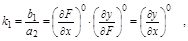 т.е. равен углу наклона a касательной к кривой
т.е. равен углу наклона a касательной к кривой 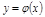 при f=f0 и в точке (x0, y0) (рис. 2.4).
при f=f0 и в точке (x0, y0) (рис. 2.4).
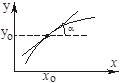
| |
Размерности коэффициентов к1 и к3 равны отклонению размерностей выходной величины к входной (к1) и к возмущающему воздействию(к3).Они характеризуют статические свойства звена и называются коэффициентами передачи.
2.2 Принцип суперпозиции
Существенное упрощение при изучении линейных систем состоит в том, что к ним применим принцип суперпозиции (принцип наложения). В соответствии с этим принципом общая реакция (изменение выходной величины) звена (системы) на несколько входных воздействий равна сумме реакций на каждое из этих воздействий. Т.е. можно определить сначала реакцию на каждое воздействие отдельно (рис. 2.5). При этом математическое описание звена будет одно и то же для всех воздействий.
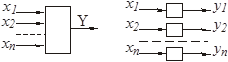
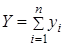 .
.
Рисунок 2.5 – Принцип суперпозиции
Это особенно важно при решении вопросов управления и регулирования в системах электроснабжения.
Кроме того, принцип суперпозиции позволяет ограничиться изучением реакции звена только на простые возмущения, а реакцию на сложные возмущения изучать как сумму реакций на простые. Чаще всего в качестве простых возмущений используют два вида воздействий: гармоническое колебание и скачок. В принципе, любой сложный по форме процесс изменения входной величины x(t) или f(t) можно представить как сумму простых.
2.3 Передаточная функция звена [2,с.18-19; 3,с.42-43; 4,с.68-71]
| |
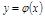 , например, алгебраическим выражением
, например, алгебраическим выражением 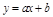 . Формально у можно выразить через х и для динамических звена или системы. Наиболее полное математическое описание динамической системы осуществляется дифференциальным уравнением. Например, дифференциальное уравнение с постоянными коэффициентами (при f=0):
. Формально у можно выразить через х и для динамических звена или системы. Наиболее полное математическое описание динамической системы осуществляется дифференциальным уравнением. Например, дифференциальное уравнение с постоянными коэффициентами (при f=0):
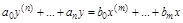 .
.
Введя оператор дифференцирования, получим символическую запись уравнения:
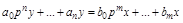 .
.
Условно выносим у и х за скобки:
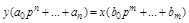 .
.
Откуда
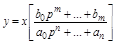 .
.
Выражение в квадратных скобках называется передаточной функцией W(p) звена (системы). С помощью передаточной функции получается самая простая форма записи дифференциального уравнения:
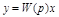 .
.
W(p) не имеет физического смысла. Это “функция” от оператора р. Но эта функция позволяет очень просто решать практические задачи и характеризует динамические и статические звенья (системы).
Для нахождения W(p) необходимо составить дифференциальное уравнение звена (системы) в операторной форме и выразить выходную величину через входную. Потом
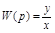 .
.
Рассмотрим уравнение вида (2.6):
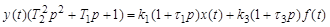 .
.
Поделив уравнение на трехчлен от р левой части получим дифференциальное уравнение относительно выходной величины:
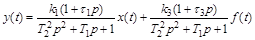 .
.
| |
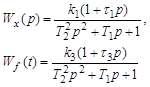
будут являться передаточными функциями звена по входной величине Wx(p) и по возмущению Wf(p). Тогда форма записи дифференциального уравнения будет иметь вид:
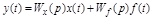 . (2.7)
. (2.7)
Передаточные функции в отличии от k1 и k3 характеризуют свойства передачи сигнала звеном в динамическом режиме (р¹0). При статическом режиме (р=0) 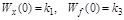 и
и
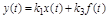 .
.
Передаточную функцию Wx(p), характеризующую статические и динамические свойства звена по входному сигналу, считают основной или главной.
Более строго передаточную функцию определяют через изображение Лапласа. Если найти изображение по Лапласу переменных величин звена
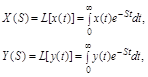
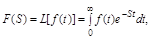
где S – комплексное число S = c+jw, то выражение
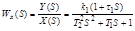
будет основной передаточной функцией звена, которое справедливо при нулевых начальных условиях.
Передаточной функцией по выбранному входному воздействию называется отношение изображения выходной величины к изображению выбранного входного воздействия при нулевых начальных условиях и при других воздействиях, равных нулю.
Уравнение примет вид:
| |
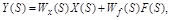
которое похоже по форме на (2.7), но оно уже алгебраическое, а не дифференциальное и описывает звено не во временной, а в комплексной области.
Пользуясь передаточными функциями, дифференциальное уравнение можно представить структурной схемой (рис. 2.6) и наоборот, по структурной схеме записать дифференциальное уравнение.
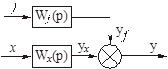
Рисунок 2.6 – Структурная схема
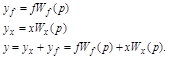
2.4 Передаточные функции типовых (элементарных) звеньев
[1,с.67-80; 2,с.25-40; 3,с.86-103]
Сложные АСУ и САР можно представить в виде соединения элементарных (типовых) звеньев, которые описываются простейшими передаточными функциями. По виду передаточных функций (или дифференциальных уравнений) и различают типы звеньев АСУ и САР. Основные типы звеньев делятся на позиционные, дифференцирующие и интегрирующие.
Знание характеристик (в т.ч. и W(p) ) типовых звеньев столь же необходимо для расчетов систем управления, как знание таблицы умножения в арифметике.
2.4.1 Позиционные звенья
Безынерционное звено. Описывается уравнением и передаточной функцией:
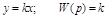 ,
,
где k – коэффициент передачи (усиления).
| |
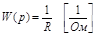 , которая не зависит от р и имеет размерность электрической проводимости.
, которая не зависит от р и имеет размерность электрической проводимости.
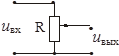
Рисунок 2.7 – Электрический аналог позиционного звена
В этом звене нет переходных процессов. Выходная величина полностью повторяет процесс изменения входной с коэффициентом k. Безынерционность звена – это идеализация, т.к. практически невозможно получить полную безынерционность. Поэтому это звено называют еще идеальным.
Инерционное (апериодическое звено первого порядка).
Описывается дифференциальным уравнением первого порядка:
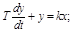
где T – постоянная времени (инерции), k – коэффициент передачи.
В символической записи:
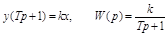 .
.
Примером апериодического звена можно считать электродвигатель, если х – управляющее напряжение, y – угловая скорость вращения вала. Это звено моделирует инерцию объектов, т.е. сглаживающее действие звена. Применяется для моделирования нагрева, изменения частоты напряжения в сети и т.д.
Звенья второго порядка. Описываются дифференциальными уравнениями второго порядка:
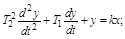
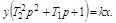 .
.
Передаточная функция:
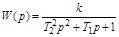
| |
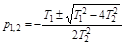 .
.
Разложив знаменатель в выражение для W(p) на сомножители можно записать:
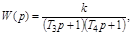
где
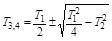 .
.
Постоянная времени T1, как и в звене первого порядка, моделирует инерцию. Чем больше T1, тем больше демпфирующее (сглаживающее) действие звена на выходную величину. Постоянная T2 характеризует раскачивающее действие звена. От их соотношения зависит вид переходного процесса на выходе.
Если 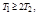 то корни р1,2 будут вещественными. В этом случае на выходе звена колебаний выходной величины не будет даже при изменении входной величины скачком. Такое звено называется апериодическим звеном второго порядка.
то корни р1,2 будут вещественными. В этом случае на выходе звена колебаний выходной величины не будет даже при изменении входной величины скачком. Такое звено называется апериодическим звеном второго порядка.
Если 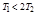 , то корни р1,2 будут комплексные.В этом случае получается колебательное звено, на выходе которого будет протекать колебательный процесс.
, то корни р1,2 будут комплексные.В этом случае получается колебательное звено, на выходе которого будет протекать колебательный процесс.
Примером таких звеньев могут быть измерительные приборы и датчики.
2.4.2 Интегрирующие звенья
Идеальное интегрирующее звено описывается дифференциальным уравнением:
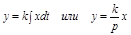 ,
,
откуда
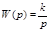 .
.
Электрическим аналогом является индуктивность с выходом по току (рис. 2.10).
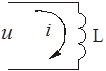
| |
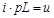 ;
; 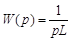 ;
; 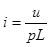 .
.
Если на индуктивность подать напряжение u скачком, то ток будет интегрироваться (нарастать) от 0до 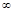 .
.
Примером может служить электродвигатель постоянного тока, выходной величиной корого которого является угол поворота, при условии безынерционности двигателя.
Инерционное интегрирующее звено описывается уравнением и передаточной функцией вида:
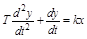
или
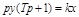 ;
;
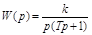 .
.
2.4.3 Дифференцирующие звенья
Идеальное дифференцирующее звено описывается:
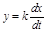
или
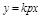 ;
;
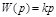 .
.
Электрический аналог – идеальный конденсатор с выходом по току (рис. 2.11).
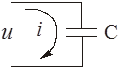
| |
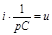 ;
; 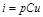 ;
; 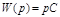 .
.
Идеальный конденсатор производит дифференцирование. Примером такого звена может служить тахогенератор, преобразующий входную величину – угол поворота вала в выходную – напряжение.
Инерционное (реальное) дифференцирующее звено.
Поскольку идеальной емкости практически не бывает, т.к. она обладает инерцией, то реальная емкость (конденсатор) описывается дифференциальным уравнением
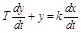
или
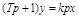 .
.
Откуда
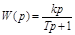 .
.
Электрическим аналогом является RC – цепь с выходом 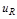 (рис. 2.12).
(рис. 2.12).
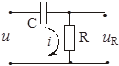
Рисунок 2.12 – Электрический аналог реального дифференцирующего звена
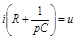 ;
; 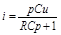 ;
;
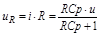 ;
; 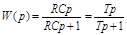 ,
,
где 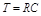 .
.
| |
2.5 Соединения звеньев и передаточные функции этих соединений
[2,с.44-47; 4,с.76-78]
Из элементарных (типовых) звеньев можно составить любую сложную систему и наоборот, зная W(p) типовых звеньев, можно найти W(p) сложной системы, а значит и записать дифференциальное уравнение системы.
Существует три основных типа соединения звеньев: последовательное, параллельное, с обратной связью и смешанное соединение.
2.5.1 Последовательное соединение
Рассмотрим вначале два звена (рис. 2.13):
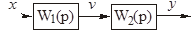
Рисунок 2.13 – Последовательное соединение звеньев
Даны 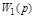 и
и 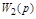 .
.
v – выходной процесс для первого звена
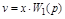
является одновременно входным для второго:
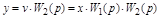 .
.
Отсюда:
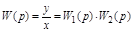 .
.
Если последовательно соединены n звеньев, то
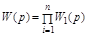 . ( 2.8)
. ( 2.8)
Таким образом, при последовательном соединении звеньев передаточные функции перемножаются.
Для цепи из последовательно соединенных звеньев общий коэффициент усиления (передачи):
| |
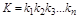 .
.
2.5.2 Параллельное соединение
Рассмотрим два звена (рис. 2.14). а и б – узлы (точки разветвления).
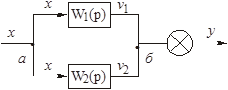
Рисунок 2.14 – Параллельное соединение звезьев
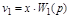 ;
;
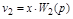 ;
;
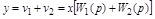 .
.
Откуда:
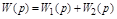 .
.
При параллельном соединении звеньев их передаточные функции складываются:
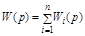 . (2.9)
. (2.9)
Общий коэффициент передачи (усиления):
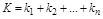 .
.
2.5.3 Звенья с обратными связями
Схема такого соединения показана на рис. 2.15.
| |
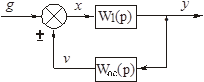
Рисунок 2.15 – Звено с обратной связью
О.С. называется отрицательной, если x = q – v и положительной, если x = q + v.
Для звена ОС входной величиной является у. Тогда выходная 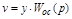 . На вход звена прямой цепи с
. На вход звена прямой цепи с 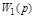 поступает процесс
поступает процесс 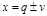 .
.
Тогда на входе:
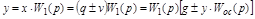 .
.
Перенесем у в левую часть:
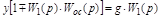 .
.
Откуда передаточная функция звена, охваченного ОС будет:
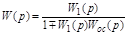 . (2.10)
. (2.10)
Знак “ – ” относится к положительной ОС, а “ + ” – к отрицательной ОС.
Общий коэффициент усиления в этом случае:
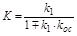 .
.
2.5.4 Смешанное соединение звеньев
В смешанном соединении могут встречаться все типы соединений звеньев (рис. 2.16). С помощью формул (2.8 - 2.10) можно найти W(p) смешанного соединения звеньев, но без перекрестных связей. Перекрестными называются связи, когда в отдельных цепях смешанного соединения звеньев присутствуют узлы и сумматоры, без переноса которых невозможно выделить обособленные типы соединений.
| |
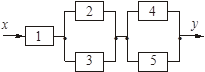
Рисунок 2.16 – Смешанное соединение звеньев
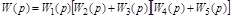 .
.
2.6 Структурные преобразования систем [2,c.50-54; 4,c.78-85]
Для удобства расчетов АС бывает необходимо преобразовать структурную схему системы к какому-либо желаемому виду. Существуют правила структурных преобразований, позволяющие формально видоизменить структурные схемы, что позволяет облегчить и упростить задачи анализа линейных АС. Формальное преобразование структурных схем заключается в их замене другими, равноценными или эквивалентными.
Любое преобразование структурной схемы сводится к перемещению или перестановке различных соседних элементов (узлов, сумматоров и звеньев). Используется при преобразовании инвертор – звено с W(p) = -1, которое изменяет знак переменной величины на противоположный и обозначается на схемах :
|
В основу правил преобразования схем положено требование сохранения неизменными входных и выходных величин преобразуемого участка схемы. Это обеспечивает эквивалентность исходной и преобразованной структурных схем в том смысле, что они соответствуют одному и тому же дифференциальному уравнению.
Приведем некоторые правила преобразования структуры разомкнутой цепи АСУ (табл. 2.1).
Пользуясь приведенными правилами, можно освободиться от перекрестных связей в составляемых структурных схемах с помощью переноса узлов и сумматоров.
2.7 Передаточные функции и дифференциальные уравнения замкнутых АС [2,с.54-59, 4,с.85-99]
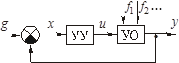
Рассмотрим функциональную схему одномерной АС, которая может состоять из цепи звеньев любой сложности (рис. 2.17).
| |
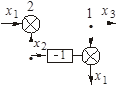
Таблица 2.1 – Правила структурных преобразований систем
| Назначение преобразования | Исходная схема | Эквивалентная схема | ||
| Перестановка узлов Перестановка сумматоров Перестановка звеньев Перенос узла с выхода на вход сумматора Перенос узла со входа на выход сумматора Перенос узла с выхода на вход звена (перенос параллельной цепи) |
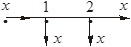
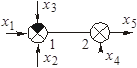
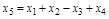

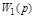 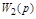
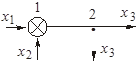
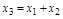
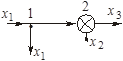
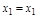
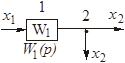
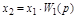
|
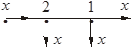
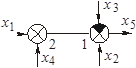
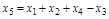

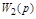 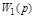
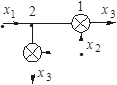
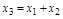
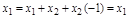
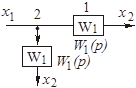
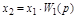
|
Продолжение таблицы 2.1
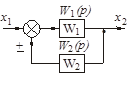
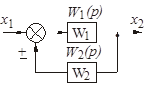
| Перенос узла со входа на выход звена (перенос параллельной цепи) Перенос сумматора со входа на выход звена (перенос воздействия) Перенос сумматора с выхода на вход звена (перенос воздействия) Замена звеньев прямой и обратной цепей Замена звена обратной связи на единичную обратную связь | 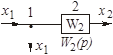
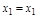
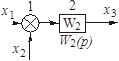
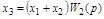
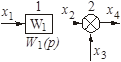
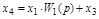
| 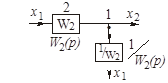
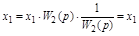
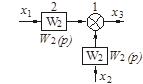
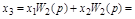
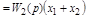
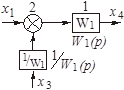
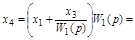
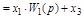
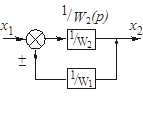 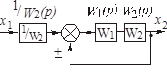
|
Получается замкнутая система с одиночной ОС, которую называют главной в отличие от местных ОС, которые могут быть внутри в составе разомкнутой цепи звеньев.
После составления дифференциальных уравнений звеньев можно найти  УУ или регулятора, а также
УУ или регулятора, а также 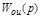 управляемого (регулируемого) объекта по управляющему воздействию и
управляемого (регулируемого) объекта по управляющему воздействию и 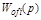
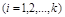 по возмущающим воздействиям.
по возмущающим воздействиям.
Дифференциальные уравнения УУ и УО
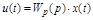 , (2.11)
, (2.11)
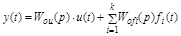 ,
,
где 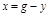 .
.
Учитывая принцип наложения, можно все возмущения заменить одним результирующим f(t).
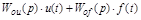 (2.12)
(2.12)
Структурная схема АС с учетом уравнений (2.11) и (2.12) будет иметь вид, показанный на рис. 2.18.
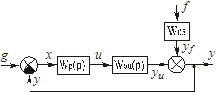
Рисунок 2.18 – Структурная блок-схема замкнутой АС
Заменив передаточные функции УУ и УО одной
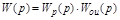 , (2.13)
, (2.13)
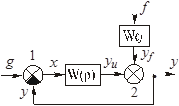
получим более компактную структурную схему (рис. 2.19).
| |
Если положить f(t) = 0 и разорвать цепь главной ОС ( y = 0 на входе АС) (рис. 2.20), то можно определить W(p) (2.13) как отношение изображений по Лапласу управляемой величины к ошибке или к задающему воздействию (так как x = g – y = g) при нулевых начальных условиях
Дата добавления: 2016-02-04; просмотров: 656;
