Обработка результатов многократных измерений
Точечная оценка результатов измерений.В практике многократных измерений наибольшее распространение получили точечные и интервальные оценки результатов измерений.
Оценку 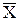 – числовой характеристики закона распределения случайной величины Xi изображаемую точкой на числовой оси, называют точечной оценкой. В отличие от числовых характеристик, оценки являются случайными величинами, значения которых зависят от числа измерений.
– числовой характеристики закона распределения случайной величины Xi изображаемую точкой на числовой оси, называют точечной оценкой. В отличие от числовых характеристик, оценки являются случайными величинами, значения которых зависят от числа измерений.
Для производственных условий наиболее характерными являются однократные измерения либо многократные измерения, причем количество многократных измерений одной и той же величины невелико (n = 5–6 измерений).
Можно говорить лишь о точечной оценке результата измерения. Число измерений невелико, поэтому отделить случайную погрешность от систематической не представляется возможным. Поскольку измерения осуществляют, как правило, в нормальных условиях, то вероятность промахов можно считать достаточно малой.
Результат измерения или среднее значение неоднократно измеряемой величины (при n = 5–6 измерений) принимается в качестве истинного, а решение о годности размера выбирают исходя из условия, что результат измерения не выходит за предел некоторой заранее заданной величины, например допуска на изготовление. При этом предельная погрешность средства измерения ±Δlim не должна превышать допускаемой погрешности измерения δ, задаваемой ГОСТ 8.051–81 в зависимости от допуска на измеряемую величину ±Δlim ≤ δ. К точечным оценкам предъявляются требования состоятельности, несмещенности и эффективности.
Оценка называется состоятельной, если при увеличении числа измерений она приближается (сходится по вероятности) к значению оцениваемого параметра, X → 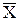 при n → ∞.
при n → ∞.
Оценка называется несмещенной, если ее математическое ожидание равно оцениваемой величине, т.е. X = 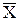 .
.
Оценка называется эффективной, когда её дисперсия является наименьшей S2 = min.
Из теории вероятностей известно, что среднее арифметическое значение измерений является несмещенной оценкой истинного значения, а СКО среднего арифметического значения – S 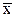 – состоятельной и эффективной и определяется по формуле (2.4).
– состоятельной и эффективной и определяется по формуле (2.4).
В этом случае точечная оценка результата измерения должна быть представлена в виде:
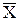 = …; S
= …; S 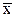 = …; n = …,
= …; n = …,
что позволяет сделать определенные, хотя и достаточно приближенные выводы о точности проведенных измерений.
Пример 3. При измерении размера вала Ø55u8 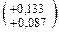 получены следующие результаты, мм:
получены следующие результаты, мм:
X1 = 55,01; Х2 = 55,13; Х3 = 55,12; Х4 = 55,12; Х5 = 55,12.
Провести точную оценку результатов измерений:
 мм;
мм;
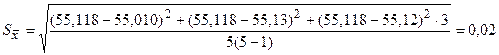 мм.
мм.
Таким образом, результат измерений
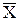 = 55,12 мм; σ
= 55,12 мм; σ 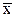 = 0,02 мм; n = 5.
= 0,02 мм; n = 5.
Результат измерения представляем в форме: 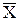 ± S
± S 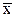 = (55,12 ± 0,02) мм.
= (55,12 ± 0,02) мм.
Интервальные оценки результатов наблюдений. Действительный размер – это размер, полученный в результате измерения с допустимой погрешностью измерения. Точечные оценки результатов измерения не позволяют в должной мере оценить достоверность измерения. Формулы (2.1) – (2.3) определяют статистические оценки размеров, т.е. приближенные значения их истинных величин, имеющих место в действительности. Степень приближения истинных величин, или точность каждой из оценок, определяется половиной ширины построенного для нее доверительного интервала.
Доверительным интервалом параметра X основной совокупности, т.е. совокупности всех возможных значений погрешности, называется интервал вида
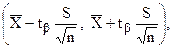
где 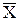 – математическое ожидание параметра X, определяемое по формуле (2.1);
– математическое ожидание параметра X, определяемое по формуле (2.1);
S – СКО, определяемое по формуле (2.2);
n – число измерений; tβ – коэффициент, определяемый из таблиц распределения Стьюдента при n ≤ 30 при заданной доверительной вероятности Р и k = n –1, называемым числом степеней свободы.
Результат измерений в этом случае записывается в виде:
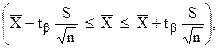
при доверительной вероятности Р.
Значения доверительных интервалов увеличиваются с увеличением доверительной вероятности Р и уменьшаются с увеличением количества наблюдений.
Пример 4. В результате измерений вала, выполненного по Ø50b10 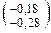 получены следующие результаты, мм:
получены следующие результаты, мм:
X1 = 49,72; Х2 = 49,74; Х3 = 49,79; Х4 = 49,80; Х5 = 49,82.
Определить доверительный интервал результатов измерений с доверительной вероятностью Р = 0,95.
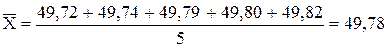 мм;
мм;
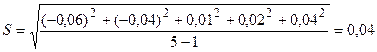 мм;
мм;
tβ = 0,27 – при k = 4, Р = 0,95.
Граница доверительного интервала
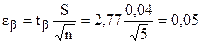 мм.
мм.
Результат измерений записывают в виде:
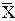 ± εβ = (49,78 ± 0,05) мм (при n = 5; Р = 0,95).
± εβ = (49,78 ± 0,05) мм (при n = 5; Р = 0,95).
Это означает, что истинное значение измеряемого размера с вероятностью 0,95 находится в пределах от 49,73 до 49,83 мм при заданном числе измерений.
Методы проверки нормального закона распределения случайных величин. При статистической обработке результатов измерений особую роль играет проверка соответствия распределения случайных величин нормальному закону, которому чаще всего подчиняются результаты большинства случайных измерений, что необходимо для обоснованного выбора доверительных границ результатов измерений и оценки точности измерений. В наибольшей степени этой цели соответствует критерий χ2 (критерий Пирсона).
При использовании критерия Пирсона количество измерений должно быть не менее 40.
Обычно принимается следующий порядок решения задачи.
1) Диапазон полученных результатов измерений делят на г интервалов шириной ΔXj (i = 1, 2, ..., г).
2) Для каждого интервала подсчитывают частоты mi, равные количеству результатов, лежащих в каждом i-м интервале.
3) Определяют частость появления величин Рi* в каждом интервале:
Рi* = mi / n,
где n – общее количество измерений, индекс «*» означает статическую оценку.
4) Находят оценку средней плотности распределения рi* случайной величины Xi в каждом интервале Δ Xi:
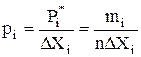 ,
,
где ni – количество измерений в i – м интервале.
5) Строят гистограмму распределения величины Xi откладывая по оси абсцисс результаты наблюдений в виде интервалов Δ Xi в порядке возрастания индекса i, а по оси ординат – оценку средней плотности распределения рi, получая тем самым прямоугольник с высотой рi*.
Естественно, что площадь всех построенных прямоугольников равна единице, поскольку в нее входят все 100 % наблюдений
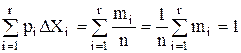 .
.
При построении гистограммы число интервалов г выбирают в зависимости от числа измерений и исходя из соотношений: при n = 40...100 г = 7...9, а при n = 100...500 г = 8...12, а масштабы по осям гистограммы рекомендуется принимать такими, чтобы отношение ее высоты к основанию составляло 5:8.
6) Соединяя середины отрезков, получают полигон распределения. Характер ломаной линии позволяет сделать предположение о виде распределения, что дает возможность с большей долей вероятности подобрать соответствующую кривую распределения.
Если СКО и математическое ожидание полигона распределения близки к значениям СКО и математическому ожиданию кривой нормального распределения, то этот вид распределения можно положить в основу гипотезы о правомерности такого предположения.
Поскольку предположение основано на результатах опытных данных случайных величин, оно должно быть подтверждено обычными методами математической статистики по критериям согласия. При числе наблюдений более 40 рекомендуется принимать критерий согласия χ2 – Пирсона.
При этом возможны два вида ошибок: ошибка первого рода, состоящая в том, что в силу случайного характера результатов измерений отвергают верную гипотезу. Вероятность ошибки первого рода называют уровнем значимости q = 1 – α., где α – уровень доверительной вероятности, и выбирают в пределах 0,05…0,10.
Принимая неверную гипотезу, совершают ошибку второго рода, – qi, значение которой колеблется в пределах 0,95…0,9 соответственно. Физический смысл которой состоит в том, что принимают ошибочное решение о несоответствии распределения случайной величины Xi правильно выбранному теоретическому распределению.
Пример 5. При контроле размера Ø 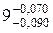 было сделано 100 измерений, причем все они оказались лежащими в диапазоне 8,911...8,927, т.е. зона разброса размера составляет 8,911 – 8,927 = 0,016 мм. В этом случае весь диапазон целесообразно распределить на 8 интервалов равной длины через 0,002 мм.
было сделано 100 измерений, причем все они оказались лежащими в диапазоне 8,911...8,927, т.е. зона разброса размера составляет 8,911 – 8,927 = 0,016 мм. В этом случае весь диапазон целесообразно распределить на 8 интервалов равной длины через 0,002 мм.
Значения величин, полученных при вычислениях, представлены в виде табл. 2.5.
Таблица 2.5
Результаты расчётов
| i | x, мм | xi+1, мм | mi | Pi* | Pi*, мм-1 |
| 8,911 | 8,913 | 0,01 | |||
| 8,913 | 8,915 | 0,05 | |||
| 8,915 | 8,917 | 0,14 | |||
| 8,917 | 8,919 | 0,27 | |||
| 8,919 | 8,921 | 0,24 | |||
| 8,921 | 8,923 | 0,18 | |||
| 8,923 | 8,925 | 0,09 | |||
| 8,925 | 8,927 | 0,02 |
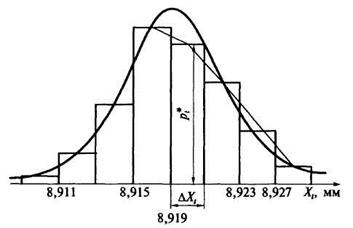
По результатам расчетов строим гистограмму и полигон распределений.
Характер распределения позволяет высказать предположение о нормальном законе распределения, однако эта гипотеза должна быть проверена по критерию χ2 – Пирсона. С этой целью:
проводят группировку данных измерений аналогично ранее описанному принципу. Если в интервале оказывается менее 5 измерений, его объединяют с соседним;
определяют среднее арифметическое значение 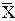 и оценку СКО S, которые принимают за параметры теоретического нормального распределения с плотностью вероятности РХ(Х);
и оценку СКО S, которые принимают за параметры теоретического нормального распределения с плотностью вероятности РХ(Х);
находят вероятность попадания в интервал результатов измерений по формуле
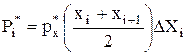 ,
,
где хi и хi+1 – результаты измерений в i-м и (i +1)-м интервалах;
вычисляют величину χi2 (i = 1, 2, …, r) для каждого интервала, затем меру расхождения χ2 при числе степеней свободы k = r – 3.
Задавая уровень значимости q = 1 – α, значения 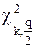 и
и 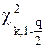 находят по таблицам интегральной функции распределения χk2 (таблицы интегральной функции χ2 – распределения Пирсона, значения χ2х, Р для различных k и P).
находят по таблицам интегральной функции распределения χk2 (таблицы интегральной функции χ2 – распределения Пирсона, значения χ2х, Р для различных k и P).
Если расчётное значение оказывается в найденных пределах – распределение результатов измерений принимают нормальным.
Пример 6. Проверить на соответствие нормальному закону полученное распределение в предыдущем примере (табл. 2.5) и представленного гистограммой (рис.2.2). Статистические характеристики наблюдений:
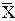 = 8,91936 мм и S = 0,0028 мм.
= 8,91936 мм и S = 0,0028 мм.
Вычисления запишем в табл. 2.6. Плотности нормированного нормального распределения Р(ti) взяты из таблицы дифференциальной функции нормированного нормального распределения, а число степеней свободы k = 8 – 2 –3 = 3, поскольку два первых и два последних интервала объединены в один (в первом и последнем частота наблюдений mi < 5).
Задавая уровень значимости q = 0,10, находим по таблице интегральной функции χ2
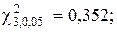

Поскольку соблюдается соотношение 0,352 < 1,1252 < 7,815, то опытное распределение можно считать нормальным.
|
|
Дата добавления: 2016-02-04; просмотров: 5371;
