Погрешности измерений
Общие положения. Процесс измерения неизбежно сопровождается ошибками, которые вызываются несовершенством измерительных средств, нестабильностью условий проведения измерений, несовершенством самого метода и методики измерений, недостаточным опытом и несовершенством органов чувств человека, выполняющего измерения, а также другими факторами.
Погрешностью измерения называется отклонение результата измерения от истинного значения измеряемой величины:
ΔХизи = Хi – Хи,
где Xj – i-е значение результата измерения;
Хи – истинное значение измеряемой величины.
Поскольку истинное значение измеряемой величины всегда остается неизвестным, за него при многократных измерениях принимается среднее арифметическое значение 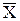 :
:
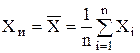 , (2.1)
, (2.1)
где n – количество проведенных измерений.
Погрешность измерения (ΔХизи), выраженная в единицах измеряемой величины, называется абсолютной. Она не всегда является информативной. Например, абсолютная погрешность 0,01 мм может быть достаточно большой при измерениях величин в десятые доли миллиметра и малой при измерениях величин, размеры которых превышают несколько метров.
Более информативной величиной является относительная погрешность, под которой понимают отношение абсолютной погрешности измерения к её истинному значению (или математическому ожиданию), %:
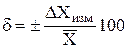 .
.
Именно относительная погрешность используется для характеристики точности измерения.
По своему характеру (закономерностям проявления) погрешности измерения подразделяются на систематические, случайные и грубые промахи.
Систематические погрешности. К систематическим погрешностям относят погрешности, которые при повторных измерениях остаются постоянными или изменяются по какому-либо закону. Систематические погрешности при измерении одним и тем же методом и одними и теми же измерительными средствами всегда имеют постоянные значения. К причинам, вызывающим их появление, относят:
– погрешности метода или теоретические погрешности;
– инструментальные погрешности;
– погрешности, вызванные воздействием окружающей среды и условий измерения.
Погрешности метода происходят вследствие ошибок или недостаточной разработанности метода измерений. Сюда же можно отнести неправомерную экстраполяцию свойства, полученного в результате единичного измерения, на весь измеряемый объект. Например, принимая решение о годности вала по единичному измерению, можно допустить ошибку, поскольку не учитываются такие погрешности формы, как отклонения от цилиндричности, круглости, профиля продольного сечения и др. Поэтому для исключения такого рода систематических погрешностей в методике измерений рекомендуется проведение измерений в нескольких местах деталей и взаимно-перпендикулярных направлениях.
К погрешностям метода относят также влияние инструмента на свойства объекта (например, значительное измерительное усилие, изменяющее форму тонкостенной детали) или погрешности, связанные с чрезмерно грубым округлением результата измерения.
Инструментальные погрешности связаны с погрешностями средств измерения, вызванными погрешностями изготовления или износом составных частей измерительного средства.
К погрешностям, вызванным воздействием окружающей среды и условий измерений, относят температуру (например, измерения ещё не остывшей детали), вибрации, нежёсткость поверхности, на которую установлено измерительное средство, и т. п.
Одним из методов обнаружения систематической погрешности может быть замена средства измерений на аналогичное в случае, если оно предположительно является источником систематической погрешности. Подобным образом можно обнаружить систематическую погрешность, вызванную внешними условиями: например, замена поверхности, на которую установлено измерительное средство, на более жёсткую.
Появление систематической погрешности можно обнаружить статистически, нанося с заданной периодичностью результаты измерений на бумагу с заданными границами (например, предельными размерами). Устойчивое движение результата измерений в сторону одной из границ будет означать появление систематической погрешности и необходимости вмешательства в технологический процесс.
Для исключения систематической погрешности в производственных условиях проводят поверку средств измерений, устраняют те причины, которые вызваны воздействиями окружающей среды, а сами измерения проводят в строгом соответствии с рекомендуемой методикой, принимая в необходимых случаях меры по ее совершенствованию.
Постоянные систематические погрешности не влияют на значения случайных отклонений измерений от средних арифметических, поэтому их сложно обнаружить статистическими методами. Анализ таких погрешностей возможен только на основании априорных знаний о погрешностях, получаемых, в частности, при поверке средств измерений. Например, при поверке средств измерений линейных величин измеряемая величина обычно воспроизводится образцовой мерой (концевой мерой длины), действительное значение которой известно. Систематические погрешности приводят к искажению результатов измерений и потому должны выявляться и учитываться при оценке результатов измерений. Полностью систематическую погрешность исключить практически невозможно; всегда в процессе измерения остается некая малая величина, называемая неисключенной систематической погрешностью. Эта величина учитывается путем внесения поправок.
Разность между средним арифметическим значением результатов измерения и значением меры с точностью, определяемой погрешностью при ее аттестации, называется поправкой. Она вносится в паспорт аттестуемого средства измерения и принимается за искомую систематическую погрешность.
Случайные погрешности. Случайные погрешности – это погрешности, принимающие при повторных измерениях различные, независимые по знаку и величине значения, не подчиняющиеся какой-либо закономерности. Причин, вызывающих случайные погрешности, может быть много; например колебание припуска на обработку, механические свойства материалов, посторонние включения, точность установки деталей на станок, точность средства измерения заготовки, изменение измерительного усилия крепления детали на станке, силы резания и др.
Как правило, индивидуальное влияние каждой из этих причин на результаты измерения невелико и не поддается оценке, тем более, что, как всякое случайное событие, оно в каждом конкретном случае может произойти или нет.
Для случайных погрешностей характерен ряд условий:
– малые по величине случайные погрешности встречаются чаще, чем большие;
– отрицательные и положительные относительно средней величины измерений, равные по величине погрешности, встречаются одинаково часто;
– для каждого метода измерений есть свой предел, за которым погрешности практически не встречаются (в противном случае эта погрешность будет грубой).
Выявление случайных погрешностей особенно необходимо при точных, например, лабораторных измерениях. Для этого используют многократные измерения одной и той же величины, а их результаты обрабатываются методами теории вероятностей и математической статистики. Это позволяет уточнить результаты выполненных измерений.
Влияние случайных погрешностей выражается в разбросе полученных результатов относительно математического ожидания, поэтому количественно наличие случайных погрешностей хорошо оценивается среднеквадратическим отклонением (СКО).
Для оценки рассеяния результатов измерений физической величины Xi относительно среднего 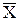 , определяемого по (2.1), СКО определяется по формуле
, определяемого по (2.1), СКО определяется по формуле
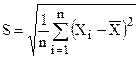 при n ≥ 20 (2.2)
при n ≥ 20 (2.2)
или
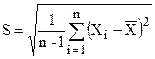 при n ≤ 20, (2.3)
при n ≤ 20, (2.3)
где n – число измерений.
Поскольку среднее значение серии измерений 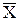 является случайным приближением к истинному значению измеряемой величины, то для оценки возможных отклонений среднего значения используется опытное СКО – S
является случайным приближением к истинному значению измеряемой величины, то для оценки возможных отклонений среднего значения используется опытное СКО – S 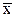 :
:
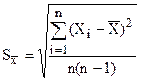 . (2.4)
. (2.4)
Величина S 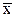 применяется при оценке погрешностей окончательного результата.
применяется при оценке погрешностей окончательного результата.
Случайные погрешности измерения, не изменяя точности результата измерений, тем не менее, оказывают влияние на его достоверность.
При этом дисперсия среднего арифметического ряда измерений всегда имеет меньшую погрешность, чем погрешность каждого определенного измерения. Из формул (2.2) и (2.3) следует, что если необходимо повысить точность результата (при исключенной систематической погрешности) в 2 раза, то количество измерений надо увеличить в 4 раза.
Грубые погрешности (промахи). Грубые погрешности – это погрешности, не характерные для технологического процесса или результата, приводящие к явным искажениям результатов измерения. Наиболее часто они допускаются неквалифицированным персоналом при неправильном обращении со средством измерения, неверным отсчетом показаний, ошибками при записи или вследствие внезапно возникшей посторонней причины при реализации технологических процессов обработки деталей. Они сразу видны среди полученных результатов, так как полученные значения отличаются от остальных значений совокупности измерений.
Если в процессе измерений удается найти причины, вызывающие существенные отличия, и после устранения этих причин повторные измерения не подтверждают подобных отличий, то такие измерения могут быть исключены из рассмотрения. Но необдуманное отбрасывание резко отличающихся от других результатов измерений может привести к существенному искажению характеристик измерений. Иногда при обработке результатов измерений учёт всех обстоятельств, при которых они были получены, не представляется возможным. В таком случае при оценке грубых погрешностей приходится прибегать к обычным методам проверки статистических гипотез.
Проверяемая гипотеза состоит в утверждении, что результат измерений Xi не содержит грубой погрешности, а является одним из значений случайной величины. Обычно проверяют наибольшее Хmах и наименьшее Xmin значения результатов измерений. Для проверки гипотез используются следующие критерии.
1) Если число измерений n ≤ 10, то может быть использован критерий Шовине. В этом случае грубой ошибкой (промахом) считается результат Хi если разность 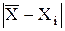 превышает значения S, определяемые в зависимости от числа измерений:
превышает значения S, определяемые в зависимости от числа измерений:
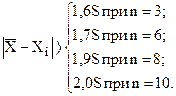
где σх – СКО, полученное по формуле (2.3).
2) Критерий Романовского, используемый при числе измерений 10 < n < 20. При этом вычисляют отношение
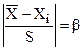
и полученное значение β сравнивают с теоретическим βт при выбираемом уровне значимости q (см. табл. 2.4). Напомним, что уровень значимости – это вероятность отвергнуть верную гипотезу при статистической проверке гипотезы. Обычно при обработке результатов измерений её значение принимают в пределах 0,05...0,1. Если β превышает βт то результат Хi считается грубой ошибкой.
Таблица 2.4
Таблица значений βт = f(n)
| Уровень значимости q | Число измерений n | ||||||
| 0,01 | 1,73 | 2,16 | 2,43 | 2,62 | 2,75 | 2,90 | 3,08 |
| 0,02 | 1,72 | 2,13 | 2,37 | 2,54 | 2,66 | 2,80 | 2,96 |
| 0,05 | 1,71 | 2,10 | 2,27 | 2,41 | 2,52 | 2,64 | 2,78 |
| 0,10 | 1,69 | 2,00 | 2,17 | 2,29 | 2,39 | 2,49 | 2,62 |
3) Критерий 3S – наиболее распространённый. Он используется, когда количество измерений n ≥ 20…50. В этом случае считается, что результат, полученный с вероятностью Р = 0,003, маловероятен и его можно квалифицировать как промах, т. е. сомнительный результат Хi должен быть исключён из измерений, если
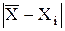 > 3S.
> 3S.
Пример 1. При измерении отверстия Ø20Н13(+0,33) получены следующие результаты:
Ø20,32; Ø20,18; Ø20,26; Ø20,21; Ø20,28; Ø20,42 мм.
Необходимо проверить является ли размер Ø20,42 мм промахом.
Поскольку n = 6, применяется критерий Шовине:
из уравнения (2.1) найдём 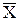
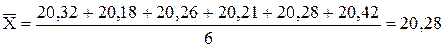 мм;
мм;
по уравнению (2.3) найдём S
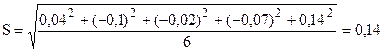 мм;
мм;
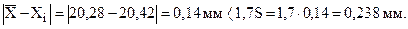
Это означает, что хотя результат и выходит за заданный предельно допустимый размер, его нельзя считать промахом. Поэтому деталь следует забраковать.
Пример 2. При измерении вала Ø40h12(-0,25) получены следующие результаты: 39,72; 39,75; 39,76; 39,80; 39,81; 39,82; 39,82; 39,83; 39,85; 39,87; 39,88; 39,88; 39,90; 39,91; 39,92; 39,92; 39,93; 39,94; 39,96; 39,98; 39,99 мм.
Поскольку результат 39,72 мм выходит за пределы наименьшего предельного размера и деталь может быть забракована, следует определить, не является ли этот размер промахом.
Так как число измерений превышает 20, можно воспользоваться критерием S. После обработки результатов измерений получаем:
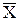 = 39,91 мм, S =0,12 мм,
= 39,91 мм, S =0,12 мм,
тогда 3S = 3·0,12 = 0,36 мм
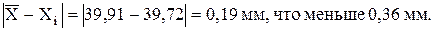
Следовательно, результат измерения 39,72 мм не может быть признан промахом и деталь должна быть забракована.
Дата добавления: 2016-02-04; просмотров: 4190;
