Виды измерений и их характеристика

В настоящее время существует множество видов измерений, различаемых физическим характером измеряемой величины и факто­рами, определяющими разнообразные условия и режимы измерений. Основными видами измерений физических величин, в том числе и линейно-угловых (ГОСТ 16263–70), являются прямые, косвен­ные, совокупные, совместные, абсолютные и относительные.

Наиболее широко используются прямые измерения, состоящие в том, что искомое значение измеряемой величины находят из опытных данных с помощью средств измерения. Линейный размер можно установить непосредственно по шкалам линейки, рулетки, штангенциркуля, микрометра, действующую силу – динамометром, температуру – термометром и т. д.

Уравнение прямых измерений имеет вид:

Q = X,

где Q – искомое значение измеряемой величины; X – значение измеряемой величины, полученное непосредственно по показа­ниям измерительных средств.

Косвенные – такие измерения, при которых искомую величину определяют по известной зависимости между этой величиной и другими величинами, полученными прямыми измерениями.

Уравнение косвенных измерений имеет вид:

Q = f (х₁, х₂, х₃, ...),

где Q – искомое значение косвенно измеряемой величины; х₁, х₂, х₃, ... – значения величин, измеряемых прямым видом измерений.

Косвенные измерения применяют в тех случаях, когда иско­мую величину невозможно или очень сложно измерить непосред­ственно, т.е. прямым видом измерения, или когда прямой вид из­мерения дает менее точный результат.

Примерами косвенного вида измерения являются установле­ние объема параллелепипеда перемножением трех линейных вели­чин (длины, высоты и ширины), определенных с использованием прямого вида измерений, расчёт мощности двигателя, определе­ние удельного электрического сопротивления проводника по его сопротивлению, длине и площади поперечного сечения и т. д.

Примером косвенного измерения явля­ется также измерение среднего диаметра наружной крепёжной резьбы методом «трех проволочек». Этот метод основан на наи­более точном определении среднего диа­метра резьбы d₂ как диаметра условного ци­линдра, образующая которого делит про­филь резьбы на равные части Р/2 (рис. 2.1):

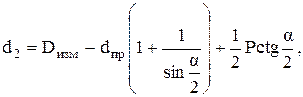
где D_изм – расстояние, включая диаметры проволочек, полученное прямыми измерениями;

d₂ – диаметр проволочки, обеспечивающий контакт с профилем резьбы в точках, лежащих на образующей d₂;

α – угол профиля резьбы;

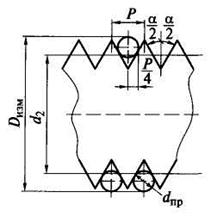Р – шаг резьбы.

Совокупные измерения осуществляют одновременным измерением нескольких одноименных величин, при которых искомое значе­ние находят решением системы уравнений, получаемых при пря­мых измерениях различных сочетаний этих величин. Примером совокупных измерений является калибровка гирь набора по извест­ной массе одной из них и по результатам прямых сравнений масс различных сочетаний гирь.

Например, необходимо произвести калибровку гарь массой 1; 2; 5; 10 и 20 кг. Образцовой принимается гиря 1 кг, обозначенная 1_об.

Проведем измерения, меняя каждый раз комбинацию гирь:

1 = 1₀₆ + а; 1 + l_об = 2 + b; 2 = 2 + с; 1+2 + 2 = 5 + d и т. д.

Буквы а, b, с, d – неизвестные значения грузиков, которые приходится прибавлять или отнимать от массы гири. Решив систе­му уравнений, можно определить значение каждой гири.

Совместные измерения – одновременные измерения двух или нескольких неодноимённых величин для нахождения зависимости между ними, например измерения объема тела, производимые с измерениями различных температур, обусловливающих изменение объема этого тела.

К числу основных видов измерений, по признаку характера результатов измерения для разнообразных физических величин, относятся абсолютные и относительные измерения.

Абсолютные измерения основаны на прямых измерениях одной или нескольких физических величин. Примером абсолютного из­мерения может служить измерение диаметра или длины валика штангенциркулем или микрометром, а также измерение темпера­туры термометром.

Абсолютные измерения сопровождаются оценкой всей измеря­емой величины.

Относительные измерения основаны на измерении отношения измеряемой величины, играющей роль единицы, или измерении величины по отношению к одноименной величине, принимаемой за исходную. В качестве образцов часто используют образцовые меры в виде плоскопараллельных концевых мер длины.

Примером относительных измерений могут служить измерения калибров пробок и скоб на горизонтальном и вертикальном опти­метрах с настройкой измерительных приборов по образцовым ме­рам. При использовании образцовых мер или образцовых деталей относительные измерения позволяют повысить точность результа­тов измерений по сравнению с абсолютными измерениями.

Помимо рассмотренных видов измерения по основному при­знаку – способу получения результата измерения виды измерений классифицируют также по точности результа­тов измерения – на равноточные и неравноточные, по числу изме­рений – на многократные и однократные, по отношению к изме­нению измеряемой величины во времени – на статические и ди­намические, по наличию контакта измерительной поверхности сред­ства измерения с поверхностью изделия – на контактные и бес­контактные и др.

В зависимости от метрологического назначения измерения де­лят на технические – производственные измерения, контрольно-поверочные и метрологические – измерения с предельно возмож­ной точностью с использованием эталонов с целью воспроизведе­ния единиц физических величин для передачи их размера рабочим средствам измерения.

Методы измерений

В соответствии с РМГ 29–99, к числу основных методов изме­рений относят метод непосредственной оценки и методы сравне­ния: дифференциальный, нулевой, замещения и совпадений.

Непосредственный метод – метод измерений, в котором значе­ние величины определяют непосредственно по отсчетному устрой­ству измерительного прибора прямого действия, например измере­ния вала микрометром и силы – механическим динамометром.

Методы сравнения с мерой – методы, при которых измеряемая величина сравнивается с величиной, воспроизводимой мерой:

дифференциальный метод характеризуется измерением разности между измеряемой величиной и известной величиной, воспроиз­водимой мерой. Примером дифференциального метода может слу­жить измерение вольтметром разности двух напряжений, из кото­рых одно известно с большой точностью, а другое представляет собой искомую величину;

нулевой метод – при котором разность между измеряемой ве­личиной и мерой сводится к нулю. При этом нулевой метод имеет то преимущество, что мера может быть во много раз меньше изме­ряемой величины, например взвешивание на весах, когда на од­ном плече находится взвешиваемый груз, а на другом – набор эталонных грузов;

метод замещения – метод сравнения с мерой, в котором изме­ренную величину замещают известной величиной, воспроизводимой мерой. Метод замещения применяется при взвешивании с поочередным помещением измеряемой массы и гирь на одну и ту же чашу весов;

метод совпадений – метод сравнения с мерой, в котором раз­ность между измеряемой величиной и величиной, воспроизводи­мой мерой, измеряют, используя совпадение отметок шкал или периодических сигналов. Примером использования данного мето­да может служить измерение длины при помощи штангенциркуля с нониусом.

В зависимости от типа, применяемых измерительных средств, различают инструментальный, экспертный, эвристический и органолептический методы измерений.

Инструментальный метод основан на использовании специальных технических средств, в том числе автоматизированных и автоматических.

Экспертный метод оценки основан на использовании суждений группы специалистов.

Эвристические методы оценки основаны на интуиции.

Органолептические методы оценки основаны на использовании органов чувств человека. Оценка состояния объекта может проводиться поэлементными и комплексными измерениями. Поэлементный метод характеризуется измерением каждого параметра изделия в отдельности. Например, эксцентриситета, овальности, огранки цилиндрического вала. Комплексный метод характеризуется измерением суммарного показателя качества, на который оказывают влияние отдельные его составляющие. Например, измерение радиального биения цилиндрической детали, на которое влияют эксцентриситет, овальность и др.; контроль положения профиля по предельным контурам и т. п.