Соотношения неопределенностей Гейзенберга. Двойственная природа частиц и статистический смысл волновой функции y(х, у, z, t), заданием которой определяется состояние частицы в пространстве

Двойственная природа частиц и статистический смысл волновой функции y(х, у, z, t), заданием которой определяется состояние частицы в пространстве, ставит вопрос о границе применимости классической физики.

В классической физике также есть границы применимости, например, понятие температуры не применимо к одной молекуле или понятие о точечной локализации не может быть применимой к определенному положению в пространстве электромагнитной волны.

В квантовой механике невозможно одновременно характеризовать микрообъект его координатами (радиус-вектором) и импульсом.

Для этого Гейзенберг ввел соотношения неопределенностей

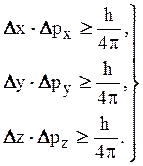(3.18)

Пример 1. Рассмотрим движение электрона в атоме.

Его положение может быть определено с точностью до размеров атома,

т. е. Dх » 10^-10 м. Скорость движение электрона в атоме v » 10⁶ м/c, его масса покоя m = 9, 11×10^-31 кг.

Тогда из соотношений неопределенностей Гейзенберга имеем

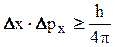или .

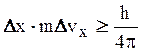Абсолютная ошибка скорости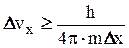

или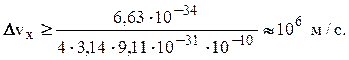

Следовательно, неопределенность нахождения скорости оказывается такого же порядка, что и сама скорость электрона в атоме.

Поэтому нельзя говорить о перемещении электрона в атоме по траектории, с точно заданной в каждой точке пространства скоростью.

Пример 2. Траектория электрона находится по следу, который фиксируется на фотопластинке.

Если размеры зерна фотоэмульсии имеют порядок Dх »10^-6 м, то положение электрона может быть найдено с точностью, определяемой линейными размерами этих зерен фотоэмульсии (классический случай).

Согласно соотношениям неопределенностей Гейзенберга (3.18) имеем

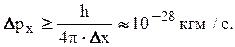
Ошибка в определении скорости электрона Dv_x = ,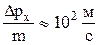

а скорость электрона v » 10⁶ .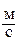

Следовательно, в этом случае можно говорить о движении электрона по траектории с точно заданной в каждой точке скоростью.

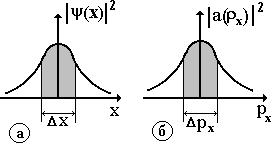Рис. 3.2

Для энергии и времени соотношение неопределенностей Гейзенберга

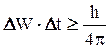(3.19)

отличается по смыслу от (3.18), поскольку время t не является динамической переменной и должно рассматриваться как параметр.

Для нестационарных состояний с характерным разбросом энергии DW под величиной Dt в (3.19) следует понимать промежуток времени, в течение которого существенно (на величину соответствующей дисперсии) изменяется среднее значение физических величин, характеризующих систему.

Вывод: Для состояния, в котором частица локализована в области пространства Dх (рис. 3.2, а), возможен разброс значений ее импульса около его среднего значения в области Dр_х (рис. 3.2, б), определяемый соотношением

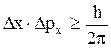. (3.20)

Таким образом, монохроматическая волна с заданным импульсом (Dр_х®0) должна заполнять полностью все пространство (Dх ® ¥).

Состояния системы, соответствующие минимуму соотношения неопределенностей, т. е. отвечающие знаку равенства в (3.20), называют когерентными состояниями, а характеристикой монохроматичности квантовых полей служит квантовая когерентность.

Соотношения неопределенностей (3.18) играют большую эвристическую роль, т. к. многие результаты задач, рассматриваемые в квантовой механике, могут быть получены и поняты на основе комбинации законов классической физики с соотношениями неопределенностей. Однако некоторые физические величины могут быть точно определены одновременно. Например, можно одновременно выполнить условия: Dх ® 0, если Dр_х ® ¥ и Dр_у ® 0, если Dу ® ¥, т. е. можно точно и одновременно измерить координату (х) и проекцию импульса на ось у (Dр_у).

Совокупность всех физических величин, которые могут быть точно и одновременно определены в данной квантомеханической системе, называют полным набором одновременно измеряемых величин.

Важный вопрос - проблема устойчивости атома. Например, электрон движется вокруг ядра атома водорода (протона) по круговой орбите радиусом r со скоростью v. По закону Кулона сила притяжения электрона к ядру 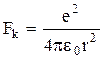, где е =½q_e½= q_p - заряд электрона и протона по абсолютной величине. Центростремительное (нормальное) ускорение электрона на орбите 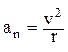. По второму закону Ньютона 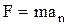, где m - масса электрона.

Роль центростремительной силы выполняет кулоновская сила,

т. е. 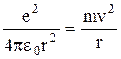. Тогда радиус орбиты 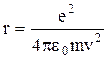может быть сколь угодно малым, если v достаточно высокая. Согласно квантовой теории должно выполняться соотношение неопределенностей.

Если принять неопределенность положения электрона в пределах радиуса его орбиты за r, а неопределенность скорости - в пределах v, т. е. неопределенность импульса в пределах Dр = mv, то mvr ³ .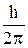

Следовательно, 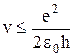и ,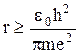

т. е. движение электрона по орбите r £ а_Б = 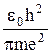» 5,5×10^-11 м невозможно.

Значит, электрон не может упасть на ядро, - атом устойчив.

Величина а_Б и является радиусом атома водорода (боровским радиусом).

Таким образом, квантовомеханические представления впервые дали возможность теоретически оценить размеры атома, выразив его через мировые постоянные.