Природа волн де Бройля

Волны де Бройля

При возрастании частоты света его волновые свойства обнаружить все труднее. Де Бройль предположил, что двойственная природа света характерна не только для света (поток фотонов), но и для всех элементарных частиц: электронов, протонов, нейтронов и др. Если импульс фотона

р_ф = h/l, (3.1)

имеет универсальный характер для любых волновых процессов, происходящих с частицами, то можно найти длину волны частиц (волну де Бройля)

l = h/p = h/mv, (3.2)

где m - масса частицы; v - ее скорость (v < c).

Если частица имеет кинетическую энергию

W_k = mv²/2 = p²/(2m), (3.3)

то ее импульс 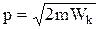. (3.4)

Поэтому формула (8.2) принимает вид

l = h / 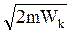. (3.5)

Например, для электрона (заряд |q_e|) ускоренного в электрическом поле с разностью потенциалов Dj, согласно закону сохранения энергии, имеем

mv²/2 =½q_e½Dj. (3.6)

С учетом этого длину волны электрона [формула (8.5)] можно найти по выражению l = h / 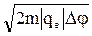. (3.7)

Формула де Бройля была подтверждена в опытах Дэвиссона и Джермера, которые наблюдали дифракцию электронов при их рассеянии на монокристаллическом никеле (фольга) 2dsinq = nl, (3.8)

Рис. 3.1

где d - период кристаллической решетки никеля; q - угол рассеяния электронов; n = 1, 2, 3, ... - порядок дифракционного максимума; l - длина волны электрона.

При Dj = 54 В [по формуле (3.7)] электрон имеет длину волны l = 1,67×10^-10 м. При n = 1 [по формуле (3.8)] имеем l = 1,65×10^-10 м, что подтверждает справедливость теории. При облучении пучком электронов тонких поликристаллических пленок (h = 10^-7 м) на экране наблюдалась дифракционная картина в виде чередующихся концентрических колец максимумов и минимумов (рис. 3.1). Позднее наблюдали дифракцию нейтронов, протонов и др. элементарных частиц, что убедительно доказывает справедливость формулы де Бройля.

Природа волн де Бройля

При движении свободного электрона с длиной волны l он характеризуется энергией

e = W = hn. (3.9)

В векторной форме формулу де Бройля запишем в виде

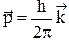, (3.10)

где 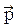- вектор импульса электрона; 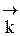- волновой вектор (модуль k = ).

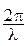При наличии у среды дисперсии необходимо учитывать фазовую v_ф и групповую u скорости, связь между которыми определяется формулой

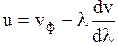, (3.11)

где .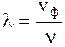

Используя формулы

W = hn, k = , ,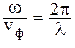

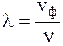имеем для фазовой скорости частицы

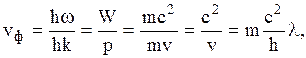(3.12)

где W - полная энергия частицы; v - скорость движения частицы; w = 2pn - циклическая частота.

Следовательно, любые волны де Бройля испытывают дисперсию, т. к. v_ф ~l.

Групповую скорость волн де Бройля найдем по формуле

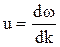, т. е.

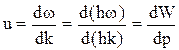. (3.13)

Для свободной частицы формула

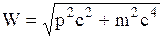(3.14)

связывает полную энергию W частицы с ее импульсом p и массой m частицы.

Следовательно, групповая скорость волн де Бройля

,

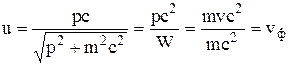т. е. u = v_ф , (3.15)

Установлено, что распространение волн де Бройля не связано с распространением в пространстве электромагнитных волн, каких-либо других, известных ранее. Волны де Бройля (волны материи), связанные с движением частиц вещества, имеют квантовую природу, не знающую аналогов в классической физике.

Ответ на вопрос о природе волн, вызванных движением частиц материи, можно найти из физического смысла амплитуды этих волн. Для этого рассматривают интенсивность J, которая пропорциональна квадрату модуля амплитуды, т. е. J ~ |A²|. (3.16)

С волновой точки зрение наличие максимума частиц в некоторых направлениях (например, дифракция электронов), обусловлено наибольшей интенсивностью волн де Бройля.

Следовательно, как показал Борн, интенсивность волн де Бройля в данной точке пространства определяет число частиц (электронов) n, попавших в эту точку за единицу времени, т. е. J ~ |A²| ~ n. (3.17)

Это положение послужило основанием для статистического, вероятностного истолкования существования волн де Бройля, а именно:

квадрат модуля амплитуды (интенсивность) волн де Бройля в данной точке пространства является мерой вероятности того, что частица находится в данной точке.