Пространственная когерентность

Формулы максимума и минимума интерференции не налагают никаких ограничений на величину оптической разности хода.

Однако интерференционную картину можно наблюдать лишь при некоторых значениях оптической разности хода d.

С увеличением d интерференционная картина ухудшается и затем исчезает совсем.

Причина заключается в том, что реальные источники света не дают идеального монохроматического излучения, а испускают лишь квазимонохроматические волны, которые обладают некоторой шириной спектральных линий: 2(dw) = 2p(dn), где n- частота световых колебаний.

Для получения интерференционной картины от двух когерентных источников монохроматического света необходимо, чтобы размеры источников не превосходили определенного предела, зависящего от расстояния между ними, взаимного расположения их и от положения экрана.

Когерентность колебаний, совершаемых в один и тот же момент времени в различных точках плоскости, перпендикулярной направлению распространения волны, называют пространственной когерентностью.

Расстояние между точками, в которых случайные изменения разности фаз достигают значения равного p, называют длиной пространственной когерентности.

Два источника, размеры и взаимное расположение которых позволяют наблюдать интерференцию от монохроматического света, называют пространственно когерентными.

Например, в опыте Юнга источником света может быть прямоугольная светящая щель шириной 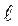. Из каждой точки щели лучи падают на щели

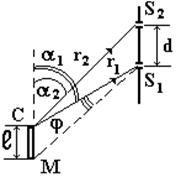Рис. 7.8

S₁ и S₂ под углами a₁ и a₂ (рис. 7.8), где сosa₁ - сosa₂ = 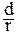(r₁ » r₂ » r); d - расстояние между щелями. Тогда j £ l / (2d), где

j = l / r (7.34)

- угловой размер источника СМ.

Следовательно, возникновение интерференционной картины зависит от степени углового расхождения лучей, освещающих щели S₁ и S₂.

Если источник света - диск, плоскость которого параллельна плоскости экрана, то при угловом размере диска j интерференция будет наблюдаться при закрытии щелей S₁ и S₂ кругом, имеющим диаметр d = λ/j.

В этом случае световые лучи, проходившие сквозь щели S₁ и S₂ - пространственно когерентны.

Минимальное сечение пучка лучей s удовлетворяющее этим условиям, называют площадью пространственной когерентности, где

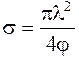. (7.35)

Когда свет строго монохроматичен, то все нарушения когерентности носят чисто пространственный характер, т. е. обусловлены различием в направлении световых лучей.

Для строго плоских волн все направления лучей одинаковы (j = 0), так как площадь когерентности s становится бесконечной.

По мере удаления от источника света угловое расхождение лучей, падающих в прибор, уменьшается, а их пространственная когерентность повышается.

Например, несмотря на большие размеры звезд свет, идущий от них, имеет высокую степень пространственной когерентности.

Световые лучи лазерного излучения, кроме того, характеризуются высокой направленностью.

Для наблюдения интерференции света используют: опыт Юнга; зеркала и бипризму Френеля; зеркало Ллойда; опыт Меслина; опыт Поля и др.

Например, в опыте Поля толщина пластинки слюды d должна быть очень мала, поэтому мнимые источники S₁ и S₂ сдвинуты друг относительно друга на величину 2d, которая во много раз меньше размеров источника света 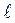. При l =5×10^-7 м, d =5×10^-7 м, r =8 м, b=30⁰

по формуле

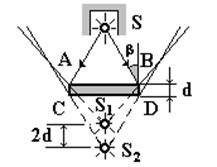Рис. 7.9

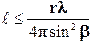, (7.36)

где r×n - оптический путь луча света (в вакууме n = 1); b - угол падения луча в т. В (рис. 7.9) находим, что 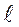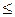8 см.

Следовательно, для получения контрастности интерференционных полос источник света должен имеет вполне разумные размеры, т. е. его можно считать светосильным.

В этом состоит основное преимущество установки.

Другое преимущество - большие апертуры интерференционных пучков, позволяющие получать интерференцию в виде цветных колец на большой площади при освещении слюды белым светом, что позволяет показать интерференцию света для большой аудитории слушателей.

Щели Юнга

Проведем расчет интерференционной картины, полученной методом Юнга (пример пространственной когерентности).

В опыте Юнга источниками когерентных световых волн являются две щели S₁ и S₂ в непрозрачном экране. Эти щели, в свою очередь, освещаются щелью S от протяженного источника света (рис. 7.10, источник света не показан).

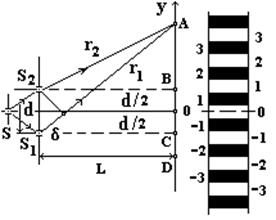Рис. 7.10

Результат интерференции в некоторой точке А на экране (рис. 7.10) будет зависеть от оптической разности хода d = Dr = (r₂ - r₁)n и длины волны падающего света l. Условия максимума и минимума интерференции, независимо от метода наблюдения, известны.

Запишем их в виде

d^мах = 2m ,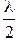

d^min = (2m+1) .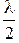

Наша задача состоит в том, чтобы, используя метод щелей Юнга, найти оптическую разность хода в интересующей нас точке на экране, например в точке А.

Если известны расстояние от щелей до экрана L, расстояние между щелями d, длина волны падающего монохроматического света l и абсолютный показатель среды n, то можно найти координаты максимума или минимума интерференционной картины в т. А.

Из треугольников S₂АВ и S₁АC, имеем

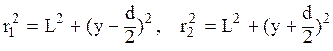(7.37)

или

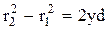. (7.38)

Из математики известно, что

,

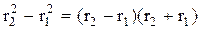где разность r₂ - r₁ = d,

а сумма

r₂ + r₁ = 2L (r » L, d << L),

т. е.

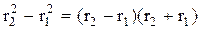= 2Ld. (7.39)

Решив совместно (7.38) и (7.39), получим

2уd » 2Ld

или у @ 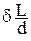. (7.40)

При d^мах = 2m 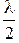получаем, что координата максимума интерференции в точке наблюдения

у^мах = m l 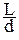, (7.41)

где m = 0, ±1, ±2, ..., - порядок интерференции.

При d^min = (2m + 1) находим, что координата минимума интерференции в точке наблюдения

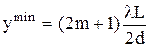. (7.42)

Таким образом, на экране будет наблюдаться интерференционная картина в виде чередующихся светлых (максимум) и темных (минимум) полос (рис. 7.10).

Распределение интенсивности света, описываемое формулой

J = 2J₀(1 + cos 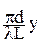), (7.43)

которая при у << L, d << L, представляет собой серию максимумов одинаковой высоты.

Это положение основано на том, что каждая щель одна равномерно освещает весь экран, что в действительности не выполняется.

Найдем ширину интерференционной полосы.

Например, максимум первого порядка (m = 1) располагается между соседними минимумами первого и второго порядков, т. е.

Dу^мах = у₂^min - у₁^min = 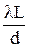, (7.44)

где

у₁^min = 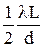, (m = 1);

у₂^min = 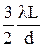, (m = 2).

Аналогично можно определить ширину интерференционного минимума, т. е. минимум любого порядка находится между соседними максимумами.

Вывод: Ширина максимума и минимума интерференции в методе щелей Юнга одинакова.

Если щели освещаются белым светом, то на экране все максимумы образуют цветной спектр от красного до фиолетового, причем внутренний цвет - фиолетовый, а внешний - красный, кроме максимума нулевого порядка, где все цвета, складываясь, образуют белый свет.