Понятие случайного события и вероятности

Опасность – это такая ситуация, при которой возникают опасные факторы, которые оказывают негативное воздействие на природные объекты и/или население. Появлению опасных ситуаций способствуют какие-то процессы и явления, связанные с деятельностью человека, или природные явления. Опасные факторы являются следствием деятельности человека или природных явлений и могут накапливаться постепенно (как, например, загрязнение химическими веществами) или проявляться внезапно, например, при взрыве. В любом случае и опасности, и опасные ситуации и опасные факторы возникают и действуют в пространстве и во времени и их возникновение связано с множеством разных случайных событий и процессов. Опасность, связанная с конкретным событием или процессом, представляет собой вероятность проявления данного события или процесса в данном месте и в данное время. Поэтому основным математически аппаратом, используемым при анализе опасностей и риска, является теория вероятностей (Бронштейн И.Н., Семендяев К.А., 1986).

Основными понятиями в теории вероятностей являются случайное событие и вероятность.

Случайное событие – это такое событие, которое может произойти или не произойти при осуществлении определенной совокупности условий. Каждое осуществление совокупности условий, которые могут вызвать совершение случайного события, называют испытанием (опытом).

Несколько событий образуют полную группу, если в результате каждого испытания обязательно должно произойти одно из них.

События называют совместимыми (совместными), если они могут произойти одновременно.

Несколько событий называются попарно несовместимыми, если никакие два из них не могут произойти одновременно.

Противоположными называются два несовместимых события, образующих полную группу. Событие, противоположное событию А, обозначается 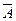(т.е. «не А»). Например, при метании монеты возможны два события – выпадение или орла или орешки. Эти два результата в данном примере составляют полную группу событий, так как являются несовместимыми и противоположными.

Несколько событий называются равновозможными, если по условиям симметрии есть основания считать, что ни одно из этих событий не является более возможным, чем другое. При метании монеты выпадение орла или орешки выступают равновозможными событиями.

Если полная группа состоит из N равновозможных попарно несовместимых случайных событий, то каждому из событий приписывают вероятность, равную 1/N.

Классическое определение вероятности формулируется в следующем виде:

Если результаты испытания можно представить в виде полной группы N равновозможных попарно несовместимых событий, и если некоторое событие А появляется в M случаях, то вероятность события А равна

P(A)=M/N. (2.12.1)

Вероятность достоверного события A (т.е. события, которое в результате любого испытания должно произойти обязательно) равна 1: P(A)=1. Можно сказать, что вероятность достоверного события A принимается за единицу измерения вероятности. Если P(A)=0 , то событие наверняка не произойдёт.

В разделе 2.11 было показано, что все возможные события могут быть представлены в виде карт. Карта на языке теории вероятностей представляет собой выборочное пространство. Полное выборочное пространство или генеральная совокупность есть множество всех возможных подмножеств или комбинаций рассматриваемых событий. Следовательно, если все события выборочного пространства объединены в одно событие, обозначенное S, с помощью операции ИЛИ, то его появление становится достоверным, т.е.

P(S) = 1. (2.12.2)

Это соотношение часто называют второй аксиомой теории вероятностей.

Таким образом, из классического определения, следует, что вероятность любого случайного события всегда заключена между 0 и 1:

О ≤Р(А) ≤ 1. (2.12.3)

При проведении статистических испытаний в науке (физике, биологии, медицине и т.д.) или технике, число испытаний A, как правило, ограничено. Поэтому в таких случаях определяют частость событий f(A) по формуле

f(A)=m/n, (2.12.4)

где m – число появления события А, n – общее число проведенных испытаний.

Пусть A – булевское событие, т.е. событие, могущее иметь два исхода. Определение частости f(A) может бать получено применение частости в форме

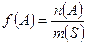, (2.12.5)

где N(A) и N(S) числа появления событий A и S соотстветственно, S – полное выборочное пространство.

При увеличении количества испытаний n до бесконечности частость появления события A стремится к вероятности Р(А) этого события, т.е.

f(A) ® Р(А), при n®¥.

При малом числе испытаний частость носит случайный характер и может сильно меняться от одной серии испытаний к другой. Если же в результате многочисленных испытаний установлено, что частость события колеблется около некоторой постоянной величины, то можно утверждать, что рассматриваемое событие имеет вероятность равную этой величине.

Применительно к задачам алгебры логики каждой логической переменной ставится в соответствие некоторая частость (относительная частота), с которой ожидается появление связанного с ней события. Если каждой логической переменной приписывать только два возможных значения 0 или 1 , то теперь частость каждого из них может иметь конкретную величину, лежащую в диапазоне между 0 и 1. По определению, данному выше, вероятность описывается частостью.

Существует два метода предсказания вероятностей: 1 – априорный, по характеру самой системы; 2 – эмпирический, по наблюдениям за прошлыми исходами. Оба метода предусматривают измерение частости, с которой ожидается появление события. В обоих случаях предполагается случайность и неизменность условий, при которых измеряется частость.

Анализируя разные опасные события и связанные с ними риски, на практике приходится складывать и умножать вероятности случайных событий. При этом, правила сложения и умножения зависят от того являются ли события совместимыми или несовместимыми, зависимыми или независимыми.