Теорема умножения вероятностей

При рассмотрении вопроса об умножении вероятностей необходимо принимать во внимание являются ли рассматриваемые события независимыми или зависимыми.

Событие А называется независимым от события В, если вероятность события не меняется от того, произошло ли событие В, или нет. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло ли событие В, или нет.

Для анализа таких событий используется понятие условной вероятности.

Условной вероятностью события А называется вероятность, вычисленная при условии, что имело место другое событие В, и обозначается Р(А/В).

По определению события А и В независимы, если появление события А не влияет на В и появление события В не влияет на появление события А. Математически это выражается следующим образом

Р(А/В) = Р(А), (2.12.19)

Р(В/А) = Р(В). (2.12.20)

Теорема умножения вероятностей формулируется следующим образом:

Вероятность произведения двух событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие произошло:

P(АВ) = P(B/A) P(A). (2.12.21)

и P(АВ) = P(A/В) P(B). (2.12.22)

Доказательство теоремы производится на основе классического определения вероятности. Пусть N – полное число всех возможных испытаний (случаев), из которых К исходов благоприятствуют событию А, а L исходов – событию В. События А и В могут быть совместимыми, поэтому возможны случаи, благоприятные им одновременно. Пусть М – число таких случаев, т.е. тех, в которых появляется событие (АВ). Тогда P(A)=K/N и P(АВ)=M/N. Вычислим условную вероятность Р(В/А). Раз известно, что событие А произошло, то из всех ранее возможных случаев остаются только те К, которые благоприятствовали этому событию. Из них М случаев благоприятны и событию В, следовательно, Р(В/А)=М/К. Если подставить полученные выражения для Р(А), Р(АВ)и Р(В/А) в формулу (2.12.21), то получим тождество: M/N=(K/N) (M/K), что и требовалось доказать.

Можно доказать, что если событие А не зависит от события В, то и событие В не зависит от события А. Это является следствием теоремы умножения вероятностей и означает, что если Р(А/В)=Р(А), то Р(В/А)=Р(В). Иными словами, зависимость или независимость событий всегда взаимны. Легко показать, что для независимых событий теорема умножения упрощается: вероятность произведения двух независимых событий равна произведению вероятностей этих событий:

Р(АВ) = Р(А) Р(В). (2.12.23)

Отсюда следует, что формула (2.12.10) теоремы сложения вероятностей для независимых событий А и В может иметь вид:

Р(А+В) = Р(А) + Р(В) - Р(А) Р(В). (2.12.24)

Теорема умножения вероятностей может быть обобщена для любого числа событий.

Расчет вероятности Р(АВ упрощается, если А и В независимы. Комбинируя выражения (2.12.19) и (2.12.22) можно получить соотношение

Р(АВ) = Р(А) (В), (2.12.25)

которое справедливо только при независимости А и В.

Можно показать, что, если A₁ и A₂ и …..A_n являются независимыми событиями, т.е. попарно независимы в смысле формул (2.12.19) и (2.12.20), то

Р(А₁ А₂…А_n)= 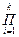P(A_i) (2.12.26)

С другой стороны, если события нельзя считать независимыми, то справедливо более сложное выражение:

Р(А₁ А₂…А_n)= P(A₁) P(A₂/A₁) P(A₃/A₁ A₂)…P(A_n/A₁ A₂…A_n-1) (2.12.27)

Условные вероятности в формуле (2.12.27) определить либо трудно, либо вообще невозможно. Поэтому необходимо доводить преобразования до такой степени, чтобы можно было использовать формулу (2.12.26).