Теоремы сложения вероятностей

Суммой нескольких случайных событий называется событие, состоящее в совершении хотя бы одного из этих событий. Если, например, событие А – выпадение орла, а событие В – выпадение орешки, то событие (А+В) состоит в том, что фиксируется любой результат. Для обозначения суммы случайных событий чаще всего используют обозначение (А+В), а также (А или В) и (АÈВ).

Произведением нескольких случайных событий называется событие, состоящее в совместном появлении всех этих событий. Помимо обозначения (А*В) или просто (АВ), используют обозначения (А и В) и (АÇВ).

Сумму и произведение случайных событий можно интерпретировать графически как показано на рис. 2.35.

Для несовместимых событий А и В в соответсвии с уравнением (2.12.1) можно написать: 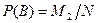, где M₁ – число случаев, благоприятствующих событию A, M₂ – число случаев, благоприятствующих событию В, N – общее число случаев.

Тогда сумма случайных несовместимых событий может быть определена как:

Р(А)+Р(В) = 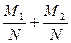= = 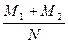Р(А+В)

или Р(А+В) = Р(А)+Р(В). (2.12.6)

Формула (2.12.6) легко обобщается для любого числа несовместимых событий:

Р(А+В+C+...) = Р(А)+Р(В)+P(C)+... (2.12.7)

Из правила сложения несовместимых событий (2.12.6) вытекает третья аксиома теории вероятностей «взаимного исключения» или несовместимости. Любые два события являются несовместимыми тогда и только тогда, когда представления их на карте оказываются неперекрывающимися выборочными пространствами. Это значит, что два события не должны иметь общих подмножеств. Если два события A₁ и A₂ несовместимы, то

P(A₁+A₂) = P(A₁) + P(A₂).
Это правило будет очень часто использоваться при расчете надёжности систем.

В разделе 2.11 введено понятие двоичного или биномиального события, называемого также булевским событием. Очевидно, что если рассматривается выборочное пространство события A, то

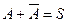(2.12.8)

Это соответствует правилам табл. 2.13. События A и 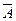не могут перекрываться. Поэтому, применяя 2.12.7, запишем

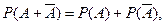
а из 2.12.8 следует, что

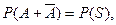
что равно единице согласно 2.12.2. Следовательно

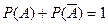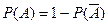и . (2.12.9)

Таким образом, если вероятность некоторой булевской переменной известна, то вероятность ее дополнения легко определяется вычитанием из 1.

Сумма случайных совместимых событий А и В определяется формулой

Р(А+В) = Р(А) + Р(B) - Р(АВ). (2.12.10)

А В А В

АА

(А+В) (А*В)

Рис. 2.36. Графическая интерпретация суммы (А+В) и произведения (А*В)

случайных событий

Действительно, обозначим через М' число случаев, в которых события А и В появляются совместно, т. е. Когда имеем их произведение (А*В). Тогда 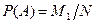, , 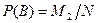Р(АВ)= М'/N . Событию (А+В) благоприятны M₁ случаев, в которых появляется событие А и в которые уже вошли М' случаев, благоприятных совмещению событий (АВ), а также (М₂ - М') случаев, в которых появляется событие В. Таким образом, событию (А+В) благоприятны М₁+(М₂ - М') случаев.

Следовательно, вероятность

Р(А+В) = (М₁+М₂ - М') /N = Р(А) + Р(В) - Р(А*В),

что и надо было доказать.

Выражение (2.12.10) легко доказывается с помощью карт. Рассмотрим простое логическое уравнение T=A+B. Карта для этого выражения представлена на рис 2.28. Если события А и В не совместимы, то в соответствии с выражением (2.12.6) Р(А+В) = Р(А)+Р(В). Но если события перекрываются, как на рис.2.28 , то такое сложение приведет к двойному учету вероятности Р(АВ). Общее выражение может быть получено для Р(А+В) из(2.12.6) поправкой на величину «лишней» вероятности Р(АВ). Для получения общего выражения эту вероятность надо вычесть из суммы вероятностей Р(А)+Р(В), т.е. мы получим уравнение Р(А+В) = Р(А)+Р(В) - Р(АВ). Таким образом, мы подтвердили справедливость уравнения (2.12.10) с помощью карт.

Формула (2.12.6) может быть обобщена на любое число несовместимых событий. Рассмотрим вероятность события Р(А₁+ А₂) Представим событие А₂ в виде двух несовместимых событий В₁ и В₂. Тогда в соответствии с (2.12.6) получим

Р(А₁+ А₂) = Р(А₁+ В₁ + В₂) = Р(А₁)+ Р(В₁ + В₂).

Но так как В₁ и В₂ также несовместимы, то

Р(А₁+ В₁ В₂) = Р(А₁) + Р(В₁) + Р(В₂).

На основании последнего выражения можно обобщить формулу для любого числа n несовместимых событий

Р(А₁+ А ₂ +…+ А _n) = 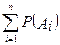(2.12.11)

Если А и В являются несовместимыми событиями, как, например, одновременное выпадение орла и орешки, то произведение их вероятностей Р(АВ)=0. В этом случае уравнение (2.12.10) преобразуется в уравнение (2.12.6).

Из теоремы сложения вытекают два следствия.

Следствие 1: Если несовместимые события образуют полную группу, то сумма вероятностей этих событий равна единице:

Р(А+В+C+...) = Р(А)+Р(В)+P(C)+... = 1. (2.12.12)

Следствие 2: Сумма вероятностей противоположных событий равна единице:

Р(А)+Р( 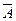) = 1. (2.12.13)

Используя правила, представленные в табл.2.14 функцию T=A+B можно представить несколькими эквивалентными выражениями:

T=A+B; (2.12.14)

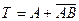; (2.12.15)

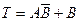; (2.12.16)

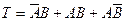. (2.12.17)

Выражения (2.12.15 – 2.12.17) не проще выражения 2.12.14, но они выражены в формах несовместимых событий. Появляется простая возможность вычислить вероятность функции суммированием вероятностей слагаемых. Таким образом, мы получаем возможность использовать три эквивалентные формы для вычисления вероятностей:

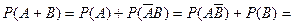
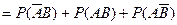(2.12.18)

Возможность использования эквивалентных выражений предоставляет большие удобства при анализе деревьев отказов.

До сих пор мы не принимали во внимание зависимость одного события от другого. При рассмотрении вопросов безопасности и оценки риска приходится рассматривать причины возникновения опасных ситуаций и их последствия. В одних случаях причиной возникновения опасной ситуации могут послужить какие-то совершенно независимые события, в других же – одни события могут возникнуть в зависимости от наличия других событий.