Анализ последствий (Стадия III)

(Хенли Э.Дж., Кумамото Х., 1984)

Взяв в качестве примера «Отчет WASH 1400», можно видеть, что на конечной стадии изучения риска производится: 1 – подсчёт количеств утечки токсичного материала и выделяемой энергии для каждого варианта развития аварии (задача 3 на рис. 2.4); 2 – прослеживание распространения токсичных продуктов, ударной волны или фронта пожара, ведущих к летальным последствиям (задача 4 на рис. 2.4); 3 – оценка воздействия на здоровье людей и повреждений материальных ценностей (задача 5 на рис. 2.4); 4 – составление общего мнения о данном производственном процессе (задача 6 на рис. 2.4) на основе сравнения с другими видами риска для общества в целом (задача 7 на рис. 2.4).

В результате решения задачи 3 составляется гистограмма вероятности в зависимости от величины утечек, показанная на рис. 2.8.

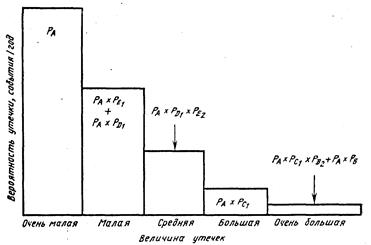
Рис. 2.8. Гистограмма частот для различных величин утечек

(Хенли Э.Дж., Кумамото Х., 1984)

В принципе эта гистограмма представляет собой кривую Фармера, которая может служить общей оценкой конструкции реактора, и является ключевой входной величиной для модели последовательности развития событий. Все другие входные величины являются специфическими для конкретного проекта и зависят от места строительства реактора, включая метеорологические и демографические данные.

Результаты решения задачи 6 показаны на рис. 2.9. При решении использовались величины, приведённые в табл. 1.1.

Как видно из приведённых данных, риск, связанный с ядерным реактором, очень мал, что подтверждается ежедневно безотказной работой сотен реакторов, находящихся в эксплуатации во всем мире.

Для вычисления величины риска необходимо знать вероятности отказов P_A, P_B, P_C и т.д. Теория надёжности позволяет определять вероятности отказов. Далее мы познакомимся с соответствующими методами.

Дерево событий, как инструмент анализа, находит применение при изучении самых разнообразных явлений. Его часто используют при изучении экономических рисков, для анализа ситуаций, встречающихся в медицинской практике, при оценке риска страховых случаев и т.п. В качестве примера рассмотрим случай из медицинской практики.

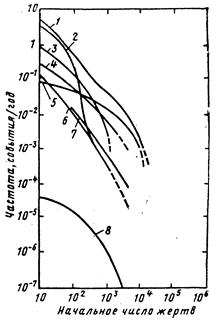Рис. 2.9. Частоты событий с человеческими жертвами, вызываемых ошибками оператора: 1 – суммарная кривая; 2 – все авиационные аварии; 3 – пожары; 4 – взрывы; 5 – аварии с плотинами; 6 – авиационные аварии на Земле; 7 – утечки хлористых веществ; 8 – 100 реакторов

Пример 2. В качестве примера построения и анализа дерева решений возьмем задачу о медицинской операции, рассмотренную Петром Александровичем Вагановым (Ваганов П.А., 1997). Предположим, что лечащий врач должен решить, следует ли делать сложную и достаточно опасную операцию пациенту, у которого подозревается серьезное заболевание, например, раковая опухоль. Если у данного пациента действительно есть опухоль, и если ему сделать операцию, то шанс на выздоровление считается равным 50%. Без операции этот шанс снижается в 10 раз и составляет всего 5%,

т.е. надеяться на выздоровление можно лишь в одном случае из 20. В то же время, если у пациента нет опухоли и он подвергнется операции, то вероятность вызванного её последствиями смертельного исхода отнюдь не мала: один шанс из 5, т.е. 20%. Если же опухоли нет и при этом не будет операции, то вероятность смерти можно считать нулевой (разумеется, в пределах сравнительно небольшого промежутка времени после принятия того или иного решения). Спрашивается, какое решение должен принять врач? Делать или не делать операцию при данных условиях? Добавим, что при построении дерева любые последствия будут приводить к одной и той же альтернативе: выздоровление или смерть (в реальной жизни бывают более сложные разветвления последствий, но мы ограничимся простым случаем).

Так как врач поставлен перед необходимостью принять одно из двух сформулированных выше решений, то дерево будет начинаться с узла решений с двумя отходящими ветвями «делать операцию» и «не делать» (см. рис. 2.10).

Эти ветви подходят к узлам случаев, каждый из которых даёт новую пару ветвей, связанных с наличием или отсутствием опухоли. Какие вероятности надо приписать ветвям «есть опухоль» и «нет опухоли»? В условии задачи ничего не сказано о надёжности диагноза, поэтому можно сделать несколько оценок этой надёжности. Пусть вероятность правильного диагноза составляет 0,75, тогда это значение нужно проставить наветви «есть опухоль», в то время как ветви «нет опухоли» будет соответствовать вероятность неправильно поставленного диагноза, т.е. 0,25.

Как показывает рис. 2.10, ветви «есть опухоль» и «нет опухоли» идут от узлов случаев и заканчиваются новыми узлами случаев, после которых каждый раз имеем разветвление «выздоровление – смерть». Однако вероятности этих исходов будут каждый раз существенно разными. Направление, задаваемое ветвями «делать операцию» и «есть опухоль», приведет к узлу случаев, после которого шансы на выздоровление и летальный исход, по условию задачи, одинаковы (вероятность 0,5). Следуя направлению «делать операцию» – «нет опухоли», подойдем к узлу, за которым вероятность выздоровления составит 0,8, а вероятность смерти – 0,2. Направление «не делать» – «есть опухоль» дает узел с разветвлением, при котором вероятность выздоровления 0,05 (один шанс из 20), а вероятность смерти 0,95 (19 шансов из 20). Наконец, направление «не делать» – «нет опухоли» приводит к последнему узлу случаев, новые ветви которого характеризуются стопроцентным выздоровлением (вероятность смерти равна нулю).

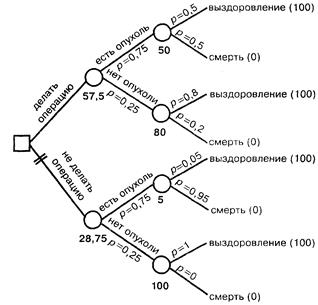
Рис. 2.10. Дерево решений в задаче о медицинской операции (Ваганов П.А., 1997)

В рассматриваемой ситуации отсутствуют количественные оценки последствий искомого решения, поэтому придется ввести условный показатель ценности этих последствий. Так как все терминалы полученного дерева представляют одну и ту же пару конечных результатов, то достаточно ввести всего две условных оценки последствий требуемого решения. Смертельный исход условимся оценивать нулём, а выздоровление – показателем, равным 100 (далее увидим, что абсолютная величина этой оценки не имеет значения, вместо 100 можно взять 1, или 10, или 1000 и т.д.).

Вспомним теперь, что анализ дерева решений ведётся от его терминалов к стволу, т.е. справа налево. Напомним также, что все узлы случаев характеризуются математическими ожиданиями показателей ценности последствий, и по ним выбирается ветвь на основе максимизации.

Начнём анализ с правого верхнего угла рис. 2.10. Находящемуся здесь узлу следует приписать математическое ожидание показателя последствий, равное сумме произведений вероятностей на соответствующие им возможные значения этого показателя: 0,5·100+0,5·0=50. Второй узел случаев, который расположен под только что рассмотренным, будет иметь математическое ожидание показателя последствий, равное 0,8·100+0,2·0=80. Для следующего узла (он находится под вторым узлом) получим значение показателя, которое составит 0,05·100+0,95·0=5. Последний узел (в нижнем правом углу рисунка) получит значение показателя ценности последствий, равное 1·100+0·0=100.

Далее необходимо рассмотреть два других узла случаев, каждый из которых связан с ветвями «есть опухоль» и «нет опухоли». Верхний из них характеризуется следующей величиной показателя последствий:
0,75·50+0,25·80=57,5. Нижний узел получит значение показателя, равное 0,75·5+0,25·100=28,75.

Теперь осталось провести максимизацию значений, полученных для только что рассмотренных узлов, поскольку в левой части дерева расположен узел решений. Наибольшей из двух величин является 57,5, её и надо оставить. Эта величина характеризует узел с ветвью «делать операцию», следовательно, ответ на заданный вопрос получен. Ветвь, идущую к узлу с меньшим значением показателя последствий, т.е. ветвь «не делать», зачеркнем (что уже сделано на рис. 2.10).

Проведённый анализ позволяет дать количественную оценку снижения риска для решения «делать операцию». Она представляет собой отношение чисел 57,5 и 28,75. Поделив первое на второе, получим 2, т.е. в данном случае операция снижает риск летального исхода в два раза. Теперь должно быть понятно, почему не имела значения абсолютная величина показателя ценности последствий решения – она сокращается при делении первой величины на вторую.

Данная задача представляет собой простую модель, иллюстрирующую анализ процесса принятия решений с привлечением метода деревьев.

Этот метод легко реализуется на современных компьютерах, так как он требует выполнения всего двух операций: подсчёта математического

ожидания и максимизации. Поэтому во многих разнообразных по характеру задачах можно строить и анализировать очень сложные деревья, с тысячами ветвей и сотнями узлов. Методом деревьев решаются и задачи, связанные с оценкой и анализом риска техногенных аварий, в том числе и разновидностей ядерного риска.