Фізичні основи пиловловлювання
Робота будь-якого пиловловлювального апарата заснована на використанні одного або декількох механізмів осаджування завислих в газах частинок [18].
Гравітаційне осадження (седиментація) відбувається внаслідок вертикального осідання частинок під дією сили ваги при проходженні їх через газоочисний апарат.
Осадження під дією відцентрової сили відмічається при криволінійному русі аеродинамічного потоку, коли розвиваються відцентрові сили, під дією яких частинки відкидаються на поверхню осадження.
Інерційне осадження відбувається в тому випадку, коли маса частинки чи швидкість її руху настільки значні, що вона не може слідувати разом з газом за лінією течії, яка охоплює перешкоду, а, пориваючись за інерцією продовжити свій рух, стикається з перешкодою і осаджується на ній.
Зачеплення (ефект дотику) спостерігається, коли відстань частинки, яка рухається з газовим потоком, від обтічного тіла дорівнює або менше її радіуса.
Дифузійне осадження. Дрібні частинки зазнають безперервну дію молекул газу, які знаходяться в броунівському русі, внаслідок якого можливе осадження цих частинок на поверхні обтічних тіл чи стінок апарата.
Електричне осадження. В процесі іонізації газових молекул електричним розрядом відбувається зарядження частинок, які містяться в газах, а потім під дією електричного поля вони осаджуються на електродах. Електричне осадження можливе і при взаємодії частинок з краплинами (чи бульбашками). Причому електричні заряди можуть бути підведені до частинок, до зрошувальної рідини чи одночасно і до частинок, і до рідини. Електричне осадження частинок може відбуватися і при проходженні аерозолю через фільтрувальні перегородки.
Крім вказаних вище основних механізмів осадження, можна перерахувати і ряд інших: термофорез, дифузіофорез, фотофорез, вплив магнітного поля, радіометричних сил тощо.
Вплив того чи іншого механізму на осадження частинок визначається цілим рядом факторів, і в першу чергу, їх розміром.
1.5.1 Гравітаційне осадження частинок. В апаратах, які викори-стовують цей принцип вловлювання пилу, осадження завислих частинок відбувається під дією сили ваги (гравітації). При падінні частинка пилу зазнає опору середовища. Найпростіше цей опір описується при прямолінійному і рівномірному русі кульової частинки, тобто в тому випадку, коли можна знехтувати турбулентністю потоку і конвенційними течіями.
Сила опору, що діє на частинку при її русі 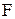 ,
, 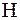 , може бути виражена рівнянням:
, може бути виражена рівнянням:
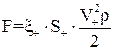 , (1.17)
, (1.17)
де 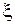 – коефіцієнт опору середовища;
– коефіцієнт опору середовища;
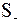 – площа перерізу частинки, перпендикулярного до напряму руху, м2;
– площа перерізу частинки, перпендикулярного до напряму руху, м2;
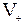 – швидкість руху частинки, м/с;
– швидкість руху частинки, м/с;
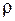 – густина газу, кг/м3.
– густина газу, кг/м3.
У випадку кульової частинки 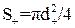 ,
,
де 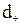 – діаметр частинки, м.
– діаметр частинки, м.
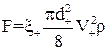 . (1.18)
. (1.18)
Коефіцієнт 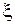 залежить від критерію Рейнольдса для частинки
залежить від критерію Рейнольдса для частинки
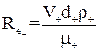 , (1.19)
, (1.19)
де 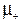 – динамічна в’язкість газів, Па∙с.
– динамічна в’язкість газів, Па∙с.
Ця залежність наведена на рис. 1.4.
Існує три різних режими руху кулеподібної частинки, кожному з яких відповідає певний характер залежності 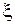 від числа Рейнольдса. Так, для ділянок з ламінарним, турбулентним і перехідним режимами (
від числа Рейнольдса. Так, для ділянок з ламінарним, турбулентним і перехідним режимами ( 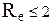 ;
; 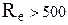 і
і 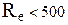 ) відповідно
) відповідно 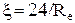 ;
; 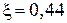 ;
; 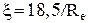 . На ділянці з ламінарним режимом руху для частинок сферичної форми опір середо-вища описується законом Стокса:
. На ділянці з ламінарним режимом руху для частинок сферичної форми опір середо-вища описується законом Стокса:
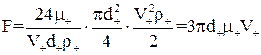 . (1.20)
. (1.20)
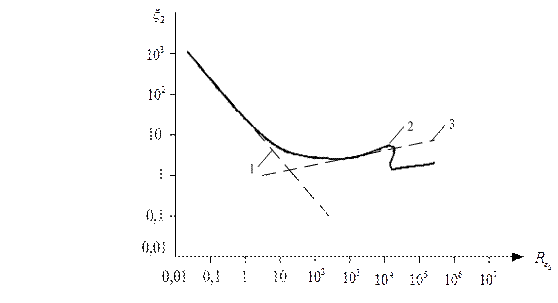
Рисунок 1.4 – Залежність коефіцієнта лобового опору кульової частинки  від критерію
від критерію  :
:
1 – область дії закону Стокса; 2 – стандартна крива; 3 – область дії формули Ньютона
Для частинок розміром 0,2…2,0 мкм в рівняння (1.20) вводиться поправка Кенінгема-Мілікена, яка враховує підвищену рухомість части-нок, розмір яких порівнюється з середньою довжиною вільного пробігу газових молекул:
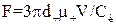 . (1.21)
. (1.21)
Поправка 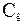 розраховується за формулою
розраховується за формулою
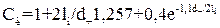 . (1.22)
. (1.22)
В свою чергу, 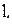 можна розрахувати за формулою
можна розрахувати за формулою
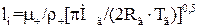 , (1.23)
, (1.23)
де 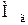 – маса 1 кмоль газів, кг/кмоль;
– маса 1 кмоль газів, кг/кмоль;
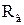 – універсальна газова постійна, рівна
– універсальна газова постійна, рівна 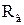 = 8314 Дж/моль∙К;
= 8314 Дж/моль∙К;
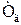 – абсолютна температура газів, К.
– абсолютна температура газів, К.
Для повітря при 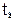 = 20°C і нормальному атмосферному тиску
= 20°C і нормальному атмосферному тиску 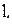 =6,5∙10-8 м.
=6,5∙10-8 м.
Відповідно до рівняння (1.22) для повітря при нормальних умовах значення поправки 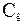 рівні:
рівні:
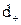 ,мкм ,мкм
| 0,003 | 0,01 | 0,03 | 0,1 | 0,3 | 1,0 | 3,0 | 10,0 |
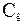
| 90,0 | 24,5 | 7,9 | 2,9 | 1,57 | 1,16 | 1,03 | 1,0 |
Розглянемо рух частинки в нерухомому середовищі під дією сили ваги (осадження). При відсутності опору середовища їх швидкість змінювалася б залежно від часу τ за законом 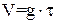 . Проте зі збільшенням швидкості буде збільшуватись величина опору середовища і відповідно зменшуватися прискорення частинки. Остаточно частинка буде рухатися з постійною швидкістю. Цю швидкість можна визначити з рівності сили опору середовища і сили ваги з врахуванням сили Архімеда:
. Проте зі збільшенням швидкості буде збільшуватись величина опору середовища і відповідно зменшуватися прискорення частинки. Остаточно частинка буде рухатися з постійною швидкістю. Цю швидкість можна визначити з рівності сили опору середовища і сили ваги з врахуванням сили Архімеда:
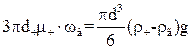 , (1.24)
, (1.24)
звідки 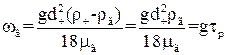 , (1.25)
, (1.25)
де ωв – швидкість витання (осадження), м/с;
τр – час релаксації частинки, с.
Величину швидкості витання ωв при гравітаційному осадженні частинок в повітрі можна визначити за допомогою графіка, наведеного на рис. 1.5.
1.5.2 Відцентрове осадження частинок. Цей метод осадження широко розповсюджений в промисловості (в циклонах, мультициклонах, ротаційних апаратах, мокрих пиловловлювачах при барботуванні).
На ділянці існування закону Стокса швидкість відцентрового осаджування кульової частинки можна розрахувати, прирівнюючи відцентрову силу F, H, яка розраховується при обертанні газового потоку, стоксовій силі опору середовища.
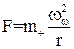 , (1.26)
, (1.26)
де 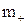 – маса частинки, кг;
– маса частинки, кг;
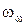 – швидкість обертання газового потоку навколо нерухомої осі, м/с;
– швидкість обертання газового потоку навколо нерухомої осі, м/с;
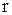 – радіус обертання газового потоку, м,
– радіус обертання газового потоку, м,
звідки 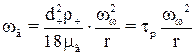 . (1.27)
. (1.27)
З рівняння (1.27) виходить, що швидкість осаджування завислих частинок у відцентрових пиловловлювачах прямо пропорційна квадрату діаметра частинок. Величина ж швидкості осаджування при відцентровому осаджуванні більша, ніж при гравітаційному в 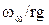 раз. Значення швидкості осаджування для частинок густиною
раз. Значення швидкості осаджування для частинок густиною 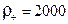 кг/м3 при відношенні
кг/м3 при відношенні 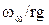 , рівному 10, 100 і 1000, наведені на рис. 1.5.
, рівному 10, 100 і 1000, наведені на рис. 1.5.
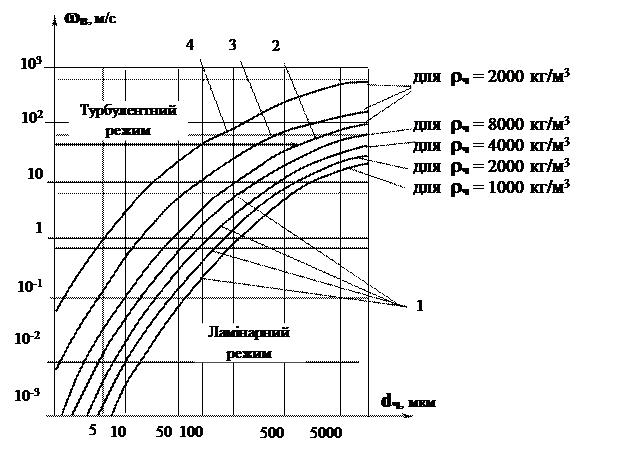
Рисунок 1.5 – Діаграма для визначення швидкості осаджування
частинок в повітрі:
1 – під дією сили ваги; 2…4 – під дією сили, яка перевищує силу
ваги відповідно в 10, 100, 1000 разів
Якщо за аналогією з вищерозглянутим гравітаційним осаджуванням виразити параметр відцентрового осадження як відношення відцентрової сили, яка діє на кулькову частинку, до сили опору середовища, то одержимо:
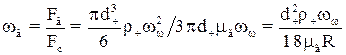 . (1.28)
. (1.28)
Відношення в правій частині рівняння (1.28) є не що інше, як критерій Стокса 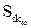 , в якому лінійний параметр – це радіус обертання газового потоку. Величину
, в якому лінійний параметр – це радіус обертання газового потоку. Величину 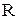 , м, можна прийняти рівною.
, м, можна прийняти рівною.
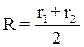 , (1.29)
, (1.29)
де 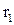 – радіус вихідної труби циклона, м;
– радіус вихідної труби циклона, м;
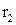 – радіус корпусу циклона, м.
– радіус корпусу циклона, м.
Найдовший шлях пилинки в радіальному напрямку рівний 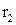 –
– 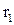 . Тоді час
. Тоді час 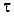 , с, необхідний для того, щоб пилинка досягла стінки циклона
, с, необхідний для того, щоб пилинка досягла стінки циклона
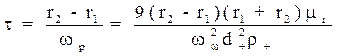 , (1.30)
, (1.30)
де ωр – швидкість руху пилинки в радіальному напрямку, м/с.
Аналіз рівняння (1.30) показує, що збільшення швидкості газового потоку поліпшує вловлювання пилу у відцентрових апаратах. Найефективніша швидкість газу на вході в апарат складає 20…25 м/с. Перевищення цієї швидкості приводить до зривання частинок пилу, які вже осіли в апараті. Якщо величина 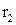 –
– 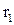 залишається постійною, але зростає абсолютне значення
залишається постійною, але зростає абсолютне значення 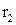 і
і 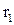 , то збільшується
, то збільшується 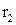 +
+ 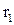 . Це приводить до збільшення необхідного для осадження пилинки часу і погіршенню коефіцієнта очищення. Звідси виходить, що для одержання високої ефективності вловлювання пилу краще застосовувати апарати малого діаметра.
. Це приводить до збільшення необхідного для осадження пилинки часу і погіршенню коефіцієнта очищення. Звідси виходить, що для одержання високої ефективності вловлювання пилу краще застосовувати апарати малого діаметра.
1.5.3 Інерційне осадження частинок. При обтіканні твердого тіла (чи краплини) запиленим потоком частинки внаслідок великої інерції продовжують рухатися поперек зігнутих ліній течії газів (рис. 1.6) і осаджуються на поверхні тіла. Таке осадження називається інерційним. Коефіцієнт ефективності інерційного осадження визначається часткою частинок, витягнутих з потоку при обтіканні ними тіла. Деколи його називають „ефективністю мішені”.
Траєкторія руху частинки в газовому потоці може бути описана рівнянням:
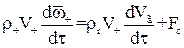 , (1.31)
, (1.31)
де 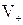 – об’єм частинки, м3;
– об’єм частинки, м3;
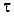 – час руху, с;
– час руху, с;
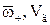 – вектор швидкості відповідно частинки і газів в місці знаход-ження частинки, м/с.
– вектор швидкості відповідно частинки і газів в місці знаход-ження частинки, м/с.
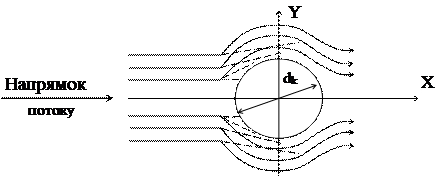 |
Рисунок 1.6 – Осадження частинок на кулі:
 рух газів;
рух газів;
----------- рух частинок
Якщо газовий потік рухається стаціонарно, а частинка настільки мала, що для Fc можна застосувати закон Стокса (з поправкою Кенінгема-Мілікена), рівняння (1.31) можна записати у такому вигляді:
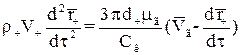 , (1.32)
, (1.32)
де 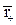 – радіус-вектор частинки, м.
– радіус-вектор частинки, м.
Рівняння (1.32) зручно привести до безрозмірного вигляду, ввівши такі значення:
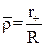 – безрозмірна координата частинки, де
– безрозмірна координата частинки, де 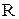 – характерний розмір обтічного тіла (наприклад, радіус кулі чи циліндра в м);
– характерний розмір обтічного тіла (наприклад, радіус кулі чи циліндра в м);
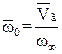 – безрозмірна швидкість газів, де
– безрозмірна швидкість газів, де 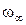 – швидкість газів, віддалених від обтічного тіла в м/с;
– швидкість газів, віддалених від обтічного тіла в м/с;
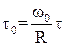 – безрозмірний час.
– безрозмірний час.
Тоді, після відповідних підстановок і спрощень, одержимо:
 , (1.33)
, (1.33)
де 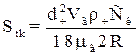 – критерій Стокса або „інерційний параметр”, який характеризує відношення інерційної сили, що діє на частинку, до сили гідравлічного опору середовища. Критерій чисельно рівний відношенню відстані, пройденої частинкою з початковою швидкістю
– критерій Стокса або „інерційний параметр”, який характеризує відношення інерційної сили, що діє на частинку, до сили гідравлічного опору середовища. Критерій чисельно рівний відношенню відстані, пройденої частинкою з початковою швидкістю 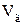 при відсутності зовнішніх сил до зупинки
при відсутності зовнішніх сил до зупинки
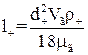
до характерного розміру обтічного тіла (наприклад, діаметра кулі чи циліндра).
Якщо рух частинки здійснюється на ділянці, де закон Стокса не можна застосувати, необхідно ввести поправку, враховуючи відношення дійсної сили опору до стоксівського опору, рівну 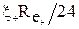
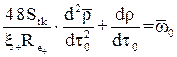 , (1.34)
, (1.34)
де 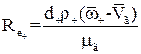 – критерій Рейнольдса для частинки.
– критерій Рейнольдса для частинки.
Критерій 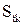 є єдиним критерієм подібності інерційного осадження. Це значить, що рівняння (1.33) застосовано до геометрично подібних систем з однаковим значенням
є єдиним критерієм подібності інерційного осадження. Це значить, що рівняння (1.33) застосовано до геометрично подібних систем з однаковим значенням 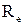 . У такому випадку подібність конфігурації лінії течії буде видержана незалежно від відмінності між швидкостями руху.
. У такому випадку подібність конфігурації лінії течії буде видержана незалежно від відмінності між швидкостями руху.
З рівняння (1.34) виходить, що при 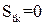 (у частинок з безмежно малою масою)
(у частинок з безмежно малою масою)
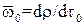 ,
,
тобто частинка точно проходить лінією течії, не дотикаючись до поверхні обтічного тіла. Очевидно таке явище буде спостерігатися і при достатньо малих значеннях критерію Стокса. Існує певне мінімальне критичне значення числа Стокса 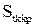 , при якому інерція частинки є достатньою, щоб перебороти збільшення її газовим потоком, і вона досягає поверхні тіла. Таким чином, захоплення частинки тілом можливе при умові:
, при якому інерція частинки є достатньою, щоб перебороти збільшення її газовим потоком, і вона досягає поверхні тіла. Таким чином, захоплення частинки тілом можливе при умові: 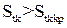 .
.
За рис. 1.6 легко прослідкувати і вплив критерію 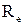 на інерційне осадження. При ламінарній течії потоку
на інерційне осадження. При ламінарній течії потоку 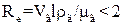 ефективність осадження не буде залежати від цього критерію, поки можна нехтувати існуванням суміжного шару навкруги обтічного тіла (в’язке обтікання). Зі збільшенням значення критерію Re при переході до турбулентного руху потоку на поверхні обтічного тіла утворюється суміжний шар, товщина якого зменшується зі збільшенням критерію
ефективність осадження не буде залежати від цього критерію, поки можна нехтувати існуванням суміжного шару навкруги обтічного тіла (в’язке обтікання). Зі збільшенням значення критерію Re при переході до турбулентного руху потоку на поверхні обтічного тіла утворюється суміжний шар, товщина якого зменшується зі збільшенням критерію 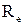 . При значеннях
. При значеннях 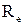 більших критичного (
більших критичного ( 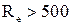 ) лінії течії сильніше вигинаються (потенціальне обтікання) і обтікають тіло на ближчій від нього відстані, внаслідок чого при тому ж значенні критерію ефективність
) лінії течії сильніше вигинаються (потенціальне обтікання) і обтікають тіло на ближчій від нього відстані, внаслідок чого при тому ж значенні критерію ефективність 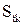 осадження буде вища. Це збільшення ефективності буде продовжуватися зі зменшенням товщини суміжного (ламінарного) шару навкруги тіла, тобто зі збільшенням критерію
осадження буде вища. Це збільшення ефективності буде продовжуватися зі зменшенням товщини суміжного (ламінарного) шару навкруги тіла, тобто зі збільшенням критерію 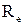 .
.
Ще складніший характер набуває суміжний шар при розвинутій турбулентній течії потоку. Тому доцільно розглядати тільки системи з однаковим значенням критерію 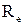 або системи, в яких режим руху потоку можна не враховувати при розрахунках.
або системи, в яких режим руху потоку можна не враховувати при розрахунках.
1.5.4 Захоплювання частинок. Розмір частинок має важливе значення при захоплюванні частинок за рахунок дотику до поверхні обтічного тіла. Якщо знехтувати інерційними ефектами і вважати, що частинка осаджується не тільки в тому випадку, коли її траєкторія пересікається з поверхнею тіла, а і у випадку проходження лінії течії на відстані від поверхні тіла, рівному її радіусу. Таким чином, ефективність зачеплення вище нуля і тоді, коли інерційне осадження відсутнє. Ефект зачеплення характеризується параметром 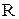 – відношенням діаметрів частинок
– відношенням діаметрів частинок 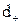 і обтічного тіла
і обтічного тіла 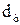 .
.
При потенційному обтіканні кулі, коли величина 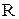 настільки мала, що можна знехтувати інерційними ефектами, ефективність зачеплення складає:
настільки мала, що можна знехтувати інерційними ефектами, ефективність зачеплення складає:
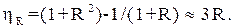 (1.35)
(1.35)
В цьому випадку для циліндра правильне співвідношення
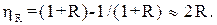 (1.36)
(1.36)
В іншому крайньому випадку, коли за рахунок великого значення інерційних ефектів траєкторії частинок, що осідають, прямолінійні, маємо такі співвідношення:
для кулі 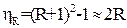 ; (1.37)
; (1.37)
для циліндра 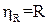 . (1.38)
. (1.38)
Таким чином, при потенційному обтіканні кулі ефективність механізму зачеплення знаходиться в межах 2R…3R, а при потенційному обтіканні циліндра – R…2R.
Для визначення ефективності осадження частинок за рахунок дотику при в’язкому обтіканні циліндра запропоновані такі рівняння:
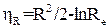 (1.39)
(1.39)
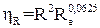 . (1.40)
. (1.40)
З цих рівнянь виходить, що ефект зчеплення стає значним при осадженні частинок на сферах з малим діаметром. Крім того, вони показують, що осадження частинок за рахунок зачеплення не залежить від швидкості газів, а в основному визначається режимом течії газового потоку.
Ефективність осадження частинок на обтічному тілі зачепленням може бути подана і в критичній формі. В цьому випадку, крім критерію Стокса, необхідно враховувати й інший комплекс, який є відношенням критеріїв
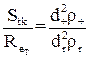 , (1.41)
, (1.41)
де 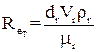 – критерій Рейнольдса для обтічного тіла.
– критерій Рейнольдса для обтічного тіла.
Тоді ефективність осадження при зачепленні може бути подана у вигляді
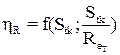 . (1.42)
. (1.42)
1.5.5 Дифузійне осадження. Частинки малих розмірів знаходяться під дією броунівського (теплового) руху молекул. Переміщення частинок в цьому випадку описується рівнянням Ейнштейна, згідно з яким середній квадрат зміщення частинок складає
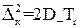 , (1.43)
, (1.43)
де 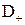 – коефіцієнт дифузії частинки, який характеризує інтенсивність броунівського руху, м2/с.
– коефіцієнт дифузії частинки, який характеризує інтенсивність броунівського руху, м2/с.
При правильності закону Стокса, коли розмір частинок більший середнього шляху пробігу молекул, коефіцієнт дифузії можна виразити як функцію розміру частинок
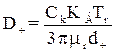 , (1.44)
, (1.44)
де 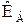 – постійна Больцмана, рівна 1,38∙10-23 Дж/К.
– постійна Больцмана, рівна 1,38∙10-23 Дж/К.
При dч > li коефіцієнт дифузії може бути розрахований за рівнянням, запропонованим Лангмюрмом
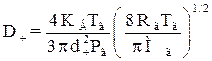 , (1.45)
, (1.45)
де 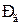 – абсолютний тиск газів, Па.
– абсолютний тиск газів, Па.
Коефіцієнт дифузії 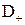 входить в безрозмірний комплекс, який характеризує відношення сил внутрішнього тертя до дифузійних сил. Цей комплекс отримав назву критерію Шмідта
входить в безрозмірний комплекс, який характеризує відношення сил внутрішнього тертя до дифузійних сил. Цей комплекс отримав назву критерію Шмідта 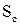 . Його деколи називають дифузійним критерієм
. Його деколи називають дифузійним критерієм 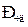 .
.
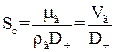 . (1.46)
. (1.46)
Другим критерієм, який застосовують у практиці дифузійних розрахунків, є критерій Пекле 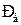 – відношення конвекційних сил до дифузійних сил
– відношення конвекційних сил до дифузійних сил
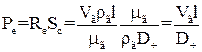 , (1.47)
, (1.47)
де 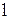 – лінійний параметр обтічного тіла.
– лінійний параметр обтічного тіла.
Величина, зворотна критерію 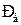 , є параметром дифузійного осад-ження і позначається через
, є параметром дифузійного осад-ження і позначається через 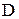 .
.
Нижче наведено значення коефіцієнта дифузії частинок, розраховані за формулою (1.44) (для повітря при н. у.) і значення критерію 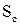 :
:
| Розмір частинок, мкм | 1,0 | 0,1 | |
| Коефіцієнт дифузії, м2/с | 2,4∙10-12 | 2,7∙10-11 | 6,1∙10-10 |
Критерій 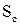
| 6,4∙106 | 5,6∙105 | 2,5∙104 |
Як видно з наведених даних, коефіцієнт дифузії різко збільшується зі зменшенням розміру частинок. Проте швидкість дифузії навіть субмі-кронних частинок надто мала порівняно з швидкістю молекул газів, тому що коефіцієнт частинок на декілька порядків менший.
Для розрахунку осадження частинок за рахунок дифузії застосо-вуються формули, одержані при розгляді процесів молекулярної дифузії.
Масову швидкість частинок 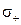 , кг/с, які дифундують на кулю розраховують за формулою:
, кг/с, які дифундують на кулю розраховують за формулою:
- при 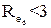 і
і 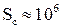
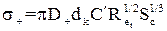 , (1.48)
, (1.48)
де 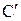 – концентрація частинок в потоці, кг/м3 ;
– концентрація частинок в потоці, кг/м3 ;
- при 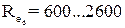 і тому ж значенні критерію
і тому ж значенні критерію 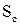
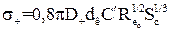 , (1.49)
, (1.49)
а при 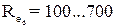 і
і 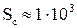
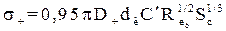 . (1.50)
. (1.50)
Для розрахунку ефективності дифузійного осадження частинок при обтіканні кулі рекомендована така формула
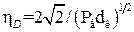 . (1.51)
. (1.51)
Рівняння для розрахунку ефективності дифузійного осадження на циліндрі при в’язкому його обтіканні має вигляд
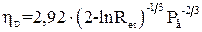 , (1.52)
, (1.52)
а при потенційному осадженні
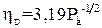 . (1.53)
. (1.53)
Згідно з вищенаведеними рівняннями, ефективність дифузійного осадження зворотно пропорційна розмірам частинок і швидкості газового потоку.
1.5.6 Осадження під дією електричних зарядів. Електричне зарядження частинок може бути здійснене трьома шляхами: при генерації аерозолю, за рахунок дифузії вільних іонів і при коронному розряді. При застосуванні перших двох способів число частинок, які одержали позитивний і негативний заряди, приблизно однакові. Коронний розряд, навпаки, приводить до зарядження частинок одним знаком. Зарядження частинок при коронному розряді здійснюється двома способами: дією електричного поля (частинки бомбардуються двома іонами, які рухаються в напрямку силових ліній поля) і дифузією іонів. Перший спосіб домінує при розмірах частинок більше 0,5 мкм, другий – при розмірах частинок менше 0,2 мкм. Для частинок діаметром 0,2…0,5 мкм ефективні обидва способи, причому мінімальна швидкість зарядження спостерігається для частинок розміром біля 0,3 мкм.
Величина заряду 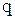 , Кл, одержуваного під дією електричного поля, електропровідної частинки сферичної форми розраховується за формулою
, Кл, одержуваного під дією електричного поля, електропровідної частинки сферичної форми розраховується за формулою
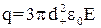 , (1.54)
, (1.54)
де 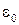 – діелектрична проникність (
– діелектрична проникність ( 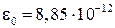 Ф/м);
Ф/м);
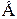 – напруженість електричного поля коронного розряду, В/м.
– напруженість електричного поля коронного розряду, В/м.
Для неелектропровідної частинки
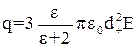 , (1.55)
, (1.55)
де 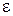 – відносна діелектрична проникність частинки.
– відносна діелектрична проникність частинки.
При дифузійному зарядженні величина 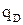 , Кл, знаходиться за формулою
, Кл, знаходиться за формулою
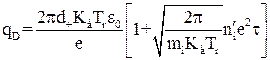 , (1.56)
, (1.56)
де 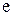 – величина заряду електрона, Кл (
– величина заряду електрона, Кл ( 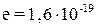 );
);
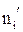 – початкова концентрація іонів коронного розряду, іони/м3;
– початкова концентрація іонів коронного розряду, іони/м3;
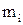 – маса іона, кг.
– маса іона, кг.
Для умов, які звичайно зустрічаються на практиці ( 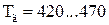 К,
К, 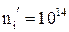 іонів/м3) рівняння (1.56) можна значно скоротити
іонів/м3) рівняння (1.56) можна значно скоротити
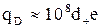 . (1.57)
. (1.57)
Таким чином, максимальна величина заряду частинок розміром більше 0,5 мкм пропорційна квадрату діаметра частинок, а частинок розміром менше 0,2 мкм – діаметру частинок.
Електростатична сила 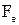 ,
, 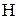 , яка діє на заряджену частинку в елек-тричному полі напруженістю
, яка діє на заряджену частинку в елек-тричному полі напруженістю 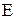 ,
, 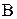 , дорівнює
, дорівнює
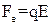 . (1.58)
. (1.58)
На ділянці застосування закону Стокса можна розраховувати, прирівнюючи кулонівську силу стоксовій силі, швидкість осадження заряджених частинок
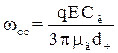 . (1.59)
. (1.59)
Значення 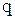 знаходиться з формул (1.54)…(1.57) залежно від влас-тивостей і розміру частинок.
знаходиться з формул (1.54)…(1.57) залежно від влас-тивостей і розміру частинок.
На методі електричного осадження частинок заснована робота електрофільтра.
Аерозоль, в якій всі частинки мають заряд одного і того ж знака, рівномірно розсіюється під дією свого власного загального заряду. Швидкість розсіювання зарядженої аерозольної хмарини описується рівнянням
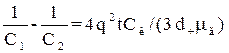 , (1.60)
, (1.60)
де 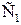 – початкова концентрація частинок, см-3;
– початкова концентрація частинок, см-3;
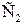 – концентрація частинок в момент часу
– концентрація частинок в момент часу 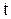 , см-3.
, см-3.
Оскільки концентрація аерозолю однакова у всіх точках у будь-який момент в процесі електростатичного розсіювання, то рух середовища не впливає на розсіювання і рівняння (1.60) справедливе для аерозолів, які знаходяться в режимі і ламінарної, і турбулентної течії.
Якщо в склад аерозолів входять і позитивно, і негативно заряджені частинки, а їх концентрації неоднакові, то частинки, які знаходяться в меншості, переміщуються до центра аерозольної хмарини, де їх концентрація поступово зростає. Густина заряду в цьому центральному ядрі починає асимптотично зменшуватися до того часу, поки воно не стане практично нейтральним. В той же самий час розсіювання зовнішньої частини аерозолів, які складаються з частинок з однойменним зарядом, продовжується.
1.5.7 Магнітні поля. Якщо тверда частинка не має природних магнітних властивостей, але при русі в газах з швидкістю 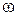 одержала електричний заряд
одержала електричний заряд 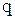 , Кл, і потім потрапила в магнітне поле напруженістю
, Кл, і потім потрапила в магнітне поле напруженістю 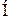 , А/м, то на частинку буде діяти сила
, А/м, то на частинку буде діяти сила 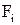 ,
, 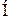 , перпендикулярна до направлення поля і до направлення руху частинки. Внаслідок цього частинка зміщується з швидкістю, яка може бути розрахована за законом Стокса:
, перпендикулярна до направлення поля і до направлення руху частинки. Внаслідок цього частинка зміщується з швидкістю, яка може бути розрахована за законом Стокса:
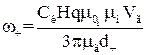 , (1.61)
, (1.61)
де 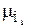 – абсолютна магнітна проникність вакууму (1,257∙10-6 Г/м);
– абсолютна магнітна проникність вакууму (1,257∙10-6 Г/м);
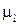 – відносна магнітна проникність.
– відносна магнітна проникність.
Швидкість зміщення в такому випадку залежить від швидкості газу; ці величини пропорційні.
Якщо малі магнітні частинки потрапляють в магнітне поле, то вони орієнтуються таким чином, що їхпротилежні кінці направляються до різних полюсів магніту. Сумарна сила, яка діє на частинку в магнітному полі, може бути подана у вигляді алгебраїчної суми сил притягання і відштовхування.
1.5.8 Акустичні поля. Частинка, яка зависла у вібрувальному середовищі, здійснює коливальний рух. Відомі спроби застосувати акустичну коагуляцію для збільшення частинок, що забезпечує їх ефективне видалення в циклоні чи в іншому пристрої для вловлювання частинок. Хоча ці спроби й привели до досягнення деяких успіхів, в цьому посібнику питання перенесення частинок в акустичному полі не розглядаються.
1.5.9 Термофорез. Термофорез – це відштовхуваннячастинок нагрі-тими тілами, викликане силами, які діють з боку газоподібної фази на нерівномірно нагріті частинки аерозолів, що знаходяться в ній. Механізм цих сил значно залежить від відношення розміру частинки і середньої довжини вільного пробігу газових молекул. При 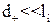 термофоретична сила
термофоретична сила 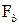 ,
, 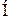 , яка діє на частинку, може бути визначена за формулою
, яка діє на частинку, може бути визначена за формулою
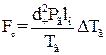 , (1.62)
, (1.62)
де 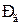 – абсолютний тиск газів, Па;
– абсолютний тиск газів, Па;
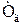 – градієнт температури в газах, К/м.
– градієнт температури в газах, К/м.
Згідно з цією формулою термофоретична сила пропорційна квадрату діаметра частинок і не залежить від тиску, тому що 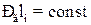 .
.
Швидкість частинок при термофорезі 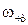 , м/с, в цьому режимі рівна
, м/с, в цьому режимі рівна
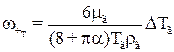 , (1.63)
, (1.63)
де 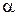 – частка розсіяних частинок молекул газа; для частинок неправильної форми і з дуже гладенькою поверхнею (аморфні чи рідкі)
– частка розсіяних частинок молекул газа; для частинок неправильної форми і з дуже гладенькою поверхнею (аморфні чи рідкі) 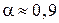 ; для частинок, утворених механічним шляхом і гострими кутами
; для частинок, утворених механічним шляхом і гострими кутами 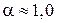 .
.
Таким чином, 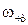 не залежить від розміру частинок і мало залежить від їх властивостей.
не залежить від розміру частинок і мало залежить від їх властивостей.
У випадку 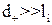 для розрахунку швидкості термофорезу можна скористатися формулою, запропонованою Ейнштейном
для розрахунку швидкості термофорезу можна скористатися формулою, запропонованою Ейнштейном
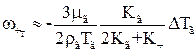 , (1.64)
, (1.64)
де 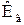 і
і 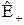 – коефіцієнт теплопровідності відповідно газів і частинки, Вт/м∙К.
– коефіцієнт теплопровідності відповідно газів і частинки, Вт/м∙К.
Тоді термофоретична сила може бути подана у вигляді
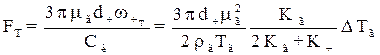 . (1.65)
. (1.65)
Рекомендовані рівняння узгоджуються з експериментальними даними для частинок з малою теплопровідністю ( 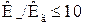 ). Для частинок з високою теплопровідністю експериментальні вимірювання термофоретичної швидкості відрізнялися в 30…100 разів. Тому Броком була рекомендована друга формула для розрахунку
). Для частинок з високою теплопровідністю експериментальні вимірювання термофоретичної швидкості відрізнялися в 30…100 разів. Тому Броком була рекомендована друга формула для розрахунку 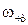 при термофорезі
при термофорезі
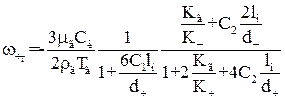 , (1.66)
, (1.66)
де 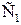 і
і 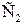 – коефіцієнти, відповідно рівні 1,875…2,48 і 1,0…1,27.
– коефіцієнти, відповідно рівні 1,875…2,48 і 1,0…1,27.
Це рівняння дає задовільні результати (помилка не перевищує 25%) для частинок з високою і низькою теплопровідністю.
Дерягіним і Бакановим була рекомендована формула для розрахунку швидкості при термофорезі частинок великих розмірів
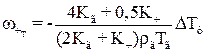 . (1.67)
. (1.67)
Експериментальний аналіз наведених вище трьох формул показав, що найкращу збіжність з практичними результатами дає рівняння (1.67).
Якщо виразити параметр осадження за рахунок термофоретичної сили як відношення цієї сили до стоксової сили опору середовища, то для найбільш розповсюдженого на практиці випадку ( 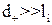 )
)
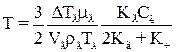 . (1.68)
. (1.68)
З врахуванням того, що теплопровідність газів значно менша теплопровідності твердих і рідких тіл, рівняння можна записати в такому вигляді:
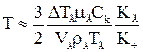 . (1.69)
. (1.69)
Якщо для розрахунку швидкості термофорезу застосувати формулу (1.67), вигляд термофоретичного параметра трохи спроститься
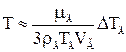 . (1.70)
. (1.70)
1.5.10 Фотофорез. Фотофорез, тобто рух частинок аерозолю, які освітлюються з однієї сторони, – це є частковий випадок термофорезу. Характер явищ, що спостерігаються, залежить від розподілення температур в освітлювальній частинці, яке в свою чергу визначається формою і розміром частинки, прозорістю і показником заломлення матеріалу. В прозорих частинках зворотна сторона може нагріватися сильніше, ніж сторона, звернена до джерела світла, внаслідок чого частинка буде рухатися за напрямом до світла. Якщо сторона, звернена до світла, гарячіша, ніж зворотна сторона, то частинка буде віддалятися від джерела світла.
1.5.11 Дифузіофорез. Дифузіофорез – це рух частинок, викликаний градієнтом концентрації компонентів газової суміші. Явище дифузіофорезу чітко проявляється в процесах випаровування і конденсації.
При випаровуванні з поверхні краплини виникає градієнт концентрації пари, але оскільки загальний тиск пари повинен залишатися постійним, відбувається гідродинамічна течія парогазової суміші, направлена перпендикулярно до поверхні випаровуваної краплини і компенсуюча дифузію газів до цієї поверхні. Ця гідродинамічна течія, названа стефанівською, може значно впливати на осадження частинок. Так, при уловлюванні частинок розпиленою водою при недонасиченні газів водяною парою стефанівська течія перешкоджає, а при перенасиченні – сприяє захвату частинок краплинами.
Математичний вираз розглянутого явища, який носить назву закону Стефана, при конденсації парів має такий вигляд
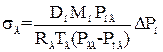 , (1.71)
, (1.71)
де 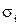 – кількість речовини, яка продифундувала за 1 с через 1 м2 поверхні, кг/м2∙с;
– кількість речовини, яка продифундувала за 1 с через 1 м2 поверхні, кг/м2∙с;
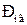 – тиск парогазової суміші, Па;
– тиск парогазової суміші, Па;
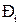 – парціальний тиск пари, Па;
– парціальний тиск пари, Па;
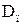 – коефіцієнт дифузії пари, м2/с;
– коефіцієнт дифузії пари, м2/с;
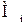 – маса 1 кмоль пари, кг/кмоль;
– маса 1 кмоль пари, кг/кмоль;
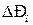 – зміна парціального тиску на осі, нормальній до поверхні краплини (плівки рідини), – градієнт парціального тиску пари.
– зміна парціального тиску на осі, нормальній до поверхні краплини (плівки рідини), – градієнт парціального тиску пари.
Рівняння Стефана справедливе і при випаровуванні: в цьому випадку змінюється тільки знак потоку речовини – з’являється мінус в правій частині рівняння (1.71).
Швидкість дифузійного руху частинки 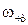 , м/с, яка враховує як дифузію самих частинок, так і стефанівську течію, при
, м/с, яка враховує як дифузію самих частинок, так і стефанівську течію, при 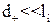 впарогазовій суміші виражається рівнянням
впарогазовій суміші виражається рівнянням
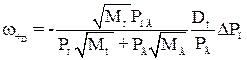 , (1.72)
, (1.72)
де 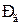 – парціальний тиск сухих газів,Па;
– парціальний тиск сухих газів,Па;
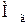 – молекулярна маса стаціонарного газу, кг/кмоль.
– молекулярна маса стаціонарного газу, кг/кмоль.
Наведене рівняння було виведене для випадку 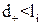 , проте воно добре описує експериментальні результати (з розходженням до 9%в тих випадках, коли
, проте воно добре описує експериментальні результати (з розходженням до 9%в тих випадках, коли 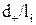 змінюються від 2 до 12).
змінюються від 2 до 12).
Дата добавления: 2016-02-02; просмотров: 2607;
