ОБРАБОТКА И АНАЛИЗ РЕЗУЛЬТАТОВ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ
Успех имитационного эксперимента с моделью системы существенным образом зависит от правильного решения вопросов обработки и последующего анализа и интерпретации результатов моделирования. Особенно важно решить проблему текущей обработки экспериментальных данных при использовании модели для целей автоматизации проектирования.
После того как компьютерный эксперимент спланирован, необходимо обеспечить эффективную обработку и представление результатов в удобном виде для анализа и последующего принятия решений. При выборе методов обработки существенную роль играют следующие три особенности компьютерного эксперимента.
1. Возможность получать при моделировании системы на компьютере большие выборки позволяет количественно оценить характеристики процесса функционирования системы, но при этом возникает проблема хранения большого объема промежуточных результатов вычислений. Эта проблема разрешима с помощью использования рекуррентных алгоритмов обработки, позволяющих вычислять оценки по ходу моделирования и использовать для расчетов (с учетом больших выборок) простые асимптотические формулы.
2. Сложность исследуемых систем не позволяет априорно судить о характеристиках процесса функционирования системы, например, о типе ожидаемого распределения выходных переменных. Поэтому при моделировании систем широко используются непараметрические оценки и оценки моментов распределения.
3. Блочность конструкции компьютерной модели и раздельное исследование блоков связаны с программной имитацией входных переменных для одной частичной модели по оценкам выходных переменных, полученных на другой частичной модели. Эти переменные следует представлять в форме, удобной для построения алгоритма их имитации.
Методы оценки
Методы оценки распределений и некоторых их моментов при достаточно большом объеме выборки, т.е. числе реализаций N, заключаются, прежде всего, в вычислении математического ожидания M[ξ]=μξ и дисперсии D[ξ]=σξ2 , т.е. соответственно первого и второго центральных моментов случайной величины ξ:
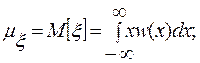
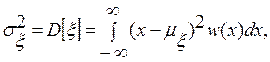
где w(x) – плотность распределения случайной величины ξ, принимающей значения x.
При проведении имитационного эксперимента со стохастической моделью системы определить эти моменты невозможно, как правило, из-за неизвестной априори (заранее) плотности распределения w(x). Поэтому при обработке результатов моделирования приходится довольствоваться лишь некоторыми оценками моментов, полученными на конечном числе реализаций N. При условии независимости наблюдений значений случайной величины ξ в качестве таких оценок используются:
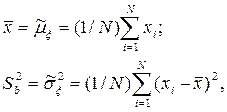
где 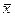 – выборочное среднее, а
– выборочное среднее, а  – выборочная дисперсия, которые используются в качестве оценок математического ожидания μξ и дисперсии σξ2соответственно.
– выборочная дисперсия, которые используются в качестве оценок математического ожидания μξ и дисперсии σξ2соответственно.
Оценки, полученные в итоге статистической обработки результатов моделирования, должны удовлетворять следующим требованиям.
1. Несмещенностьоценки означает равенство математического ожидания оценки определяемому параметру:

где 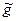 – оценка параметра g.
– оценка параметра g.
2. Эффективностьоценки означает минимальность среднего квадрата ошибки данной оценки: 
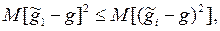
где 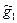 – рассматриваемая оценка;
– рассматриваемая оценка; 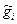 – любая другая оценка.
– любая другая оценка.
3. Состоятельностьоценки означает сходимость по вероятности при N→∞ к оцениваемому параметру:
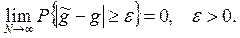
С учетом неравенства Чебышева достаточное условие выполнения этого неравенства заключается в том, чтобы
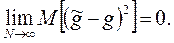
Дата добавления: 2016-02-02; просмотров: 1067;
