Линейное векторное пространство
Если система векторов x1, x2,…, xm принадлежит некоторому пространству S, то и множество векторов y, являющихся линейной комбинацией векторов xi, также образует векторное пространство, размерность которого равна максимальному числу его независимых векторов.
 .
.
Если же в этом выражении только r векторов xi являются линейно независимыми, то размерность пространства, которое можно образовать этими векторами, равна r (рангу системы векторов xi).
Пример. Рассмотрим векторы

Эти векторы являются линейно зависимыми, так как существует линейное соотношение:
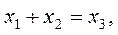
которое позволяет вектор y выразить следующим образом:
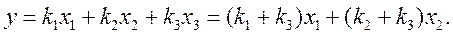
Вектор y не может содержать три независимые составляющие. Только две составляющие y могут выбираться независимо. Следовательно, размерность пространства, образуемого данными x1, x2, x3, равна двум.
В n-мерном пространстве n составляющие y могут выбираться независимо в том случае, когда вектор y образуется системой векторов, имеющих ранг n. В этом случае систему n линейно независимых векторов называют линейной оболочкой. Эту же систему линейно независимых векторов можно использовать как базис линейного векторного пространства.
Базисом пространстваназывается такая система векторов, при которой любой произвольный вектор пространства выражается в ней единственным образом в виде линейной комбинации этих (базисных) векторов.
Дата добавления: 2016-02-02; просмотров: 777;
