Определение токов к.з. без успокоительных обмоток

Определение токов короткого замыкания

Введение

Исследование переходных процессов и, в частности, режимов к. з. в синхронных генераторах по уравнениям, в которых в ка­честве переменных величин приняты мгновенные значения фаз­ных токов i_а, i_b, i_c, встречает серьезные трудности. Это связано с тем, что взаимная индуктивность обмоток статора и вращающе­гося ротора переменна, а в явнополюсной машине, кроме того, изменяются собственные и взаимные индуктивности ее фазных обмоток.

Эта задача значительно упрощается, если с помощью линейного преобразования перейти от фазных переменных к некоторым новым переменным, учитывающим особенности явнополюсной машины.

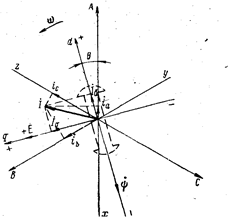
Известно, что мгновенные значения токов (или напряжений) в фазах трехфазной симметричной системы можно получить, прое­цируя звезду векторов токов (или напряжений) каждой фазы на ось ординат для последовательных моментов времени, соответ­ствующих перемещению ротора. Те же мгновенные значения фаз­ных величин можно найти, проецируя некоторый изображающий вектор трехфазной системы на оси фаз Ах, By, Сz (для каждой фазы своя ось), повернутые относительно друг друга на 120° (рис. 22.1).

Изображающий вектор 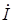раскладывается на составляющие в двухосной системе координат, жестко связанной с ротором. При этом одна из ее осей (ось d) располагается по продольной оси ротора, а вторая (ось q) - перпендикулярно к оси ротора. Тогда изображающий вектор 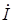представляется в виде двух составляющих: вектора продольного тока 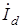и вектора поперечного тока 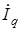. Следовательно,

.

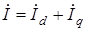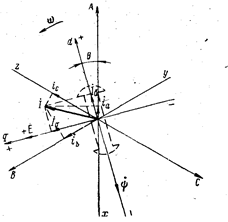
Рис. 22.1. Векторная диаграмма к преобразованию координат

Для случая, когда обмотки фаз статора соединены звездой, общая точка (нейтраль) которой изолирована, фазные токи удо­влетворяют условию

.

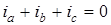Выражения, связывающие фазные токи i_a, i_b, i_c с токами I_d и I_q имеют вид

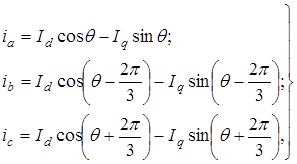(22.1)

где θ - текущий угол поворота продольной оси ротора d относи­тельно магнитной оси обмотки фазы статора А, принятой за ис­ходную.

На основании выражений (22.1) можно также выразить вели­чины I_d и I_q через токи i_a, i_b, i_c.

Сказанное выше относительно изображающего вектора тока может быть распространено и на изображающие векторы напря­жения и потокосцепления статора генератора.

Относительно новых переменных полные индуктивности фаз статора и взаимные индуктивности между ротором и статором становятся постоянными величинами, что существенно упрощает рассмотрение переходных процессов в трехфазном синхронном генераторе.

При разложении изображающих векторов на составляющие необходимо задаться положительным направлением проекций векторов, причем за положительное направление для продольных потокосцеплений принято направление по продоль­ной оси ротора вниз, а для поперечных потокосцеплений - направление по поперечной оси влево (см. рис. 22.1).

За положительное направление продольных и поперечных эдс и напря­жений генератора примем направления, совпадающие с направлениями осей d и q, т. е. продольные и поперечные эдс и напряжения будем считать положительными при отставании их от соответствующих потокосцеплений на 90°.

После перехода к новым переменным можно найти токи ста­тора по отношению эдс к полному сопротивлению внешней цепи z_ВН для стационарного режима. Для этого воспользуемся векторной диаграммой ненасыщенной неявнополюсной машины (рис. 22.2). Если принять активное сопротивление генератора равным нулю, то любая из внутренних эдс генератора будет равна геометрической сумме напряжения на зажимах генера­тора и падения напряжения в соответствующем сопротивлении.

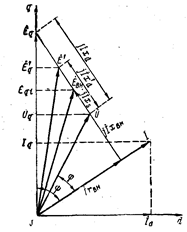
Рис. 22.2. Векторная диаграмма ненасыщенной неявнополюсной машины

Разложив ток статора на продольную и поперечную составляю­щие, получим

I_d=Isinψ, I_q=Icosψ,

после чего можно написать следующие выражения:

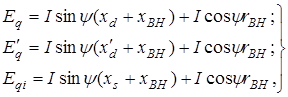(22.2)

где ψ - угол между направлениями вектора тока и осью q.

В последние выражения входят одни и те же значения токов и внешних сопротивлений. Это позволяет определить токи статора по любому из отношений эдс к соответствующему сопротивлению.

При трехфазном к. з. на зажимах машины напряжений генератора становится равным нулю, углы сдвига между эдс холостого хода и любой из внутренних эдс будут также равны нулю, а угол ψ становится равным 90°. В этом случае по обмотке статора протекает лишь продольная составляющая тока 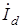, и выражения (22.2) принимают вид

Е = E_q = Ix_d;

Е' = E'_q = Ix'_d;

Е_i= E_qi = Ix_s;

откуда

I=E_q/x_d=E'/x'_d=E_i/x_s.

Чтобы решить, какую из эдс в том или другом случае брать за расчетную, вспомним, что в начальный момент к. з. в обмотке возбуждения появится дополнительный ток возбуждения Δi_в0, вызывающий скачок эдс холостого хода на величину ΔE_q0. При этом начальное значение эдс холостого хода становится равным

E_{qк.з 0}=E_q0+ΔE_q0.

Под эдс холостого хода здесь будем понимать эдс, создаваемую только током обмотки возбуждения.

Так как причина, вызывающая приращение тока Δi_в0 (внезапность появления тока к.з.), снимается, то этот ток с течением времени исчезает, вызывая постепенное уменьшение приращения эдс ΔE_q0. При установившемся режиме приращение тока Δi_в становится равным нулю, а эдс холостого хода будет равна своему начальному значению (до режима к. з.), т. е. E_q∞=E_q0; (рис. 22.3). Высказанные соображения позволяют написать выражения эдс холостого хода генератора для любого момента к. з.:

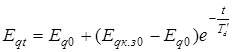, (22.3)

где T'_d - постоянная времени обмотки возбуждения при короткозамкнутой обмотке статора.

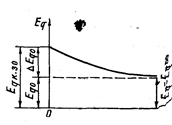
Рис.22.3. Кривая изменения эдс холостого хода при к.з.

Разделив правую и левую части выражения (22.3) на значение синхронного реактивного сопротивления x_d, получим выражение для тока к. з.

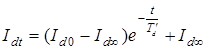(22.4)

где I_d0=E_qк.з0/x_d - начальное значение периодического тока к. з.;

I_d∞=E_q0/x_d – установившееся значение этого тока (при t→∞).

Из выражения (22.4) следует, что для определения периоди­ческой составляющей тока к. з. синхронного генератора без успокоительной обмотки достаточно знать начальное и устано­вившееся значение тока к. з. и значение T'_d. Поскольку указан­ные значения токов можно найти по любому из приведенных выше отношений E/x, если только эти величины известны, остается выяснить, какие же параметры можно считать известными при исследовании того или иного режима машины.

Для этого рассмотрим, как вычисляется ток установившегося режима.

Из выражения (22.4) следует, что ток установившегося режима определяется отношением

I_d∞=E_q∞/x_d= E_q0/x_d.

Так как эдс холостого хода генератора при установив­шемся режиме имеет такое же значение, как и до возникновения к. з., то при известном значении x_d вычисление тока I_d∞ затруднений не вызывает, поскольку в этом случае нет необходимости считаться с изменением насыщения машины. Электродвижущую силу холостого хода можно определить

по известному значению тока возбуждения до режима к. з., пользуясь характеристикой холостого хода генератора. Более того, по этому значению тока возбуждения генератора можно сразу найти установившийся ток, пользуясь характеристикой к. з. генератора.

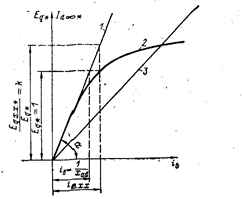
Рис. 22.4. Характеристики холостого хода и короткого замыкания синхронной машины

С целью подтверждения этих положений обратимся к рис. 22.4, где приведены характеристика холостого хода синхронной ма­шины (кривая 2) и характеристика короткого замыкания (кри­вая 3), выраженные в относительных единицах. За базисную величину эдс принято номинальное напряжение машины, а базисный ток возбуждения выбран таким образом, что угловой коэффициент tgα наклона начального участка характеристики холостого хода равен сопротивлению продольной реакции ста­тора x_ad. Проведя касательную к этой кривой холостого хода в на­чале координат, получим характеристику холостого хода генератора без учета насыщения стали (кривая 1). По этой характе­ристике легко найти эдс генератора при любом возбуждении, а по ней и ток к. з.:

I_d∞=E_q*/x_d* . (22.5)

При построении характеристики к. з. за единицу тока ста­тора принят его номинальный ток. Из этого построения следует, что ток к. з. при данном возбуждении так относится к току к. з. при возбуждении холостого хода, как относительный ток данного возбуждения к току возбу­ждения холостого хода:

,

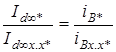откуда

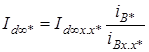. (22.6)

При возбуждении холостого хода, как следует из рис. 22.4, эдс E_q* будет равна

E_q*=x_ad* i_B*.

С учетом зависимости (22.5) ток глухого короткого замыкания определяется соотношением

.

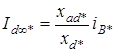В то же время из курса электрических машин известно, что величина, обратная х_d*, есть ОКЗ - отношение короткого замы­кания синхронной машины. Поэтому для произвольных значений тока возбуждения справедлива зависимость

I_d∞*=x_ad*ОКЗi_B* (22.7)

При учете насыщения величина ОКЗ должна быть увеличена в E_qx.x*=k раз. Действительно, по определению

ОКЗ = i_{B x.x} /i_Bк.з,

где i_ВК.З* - ток возбуждения, соответствующий номинальному значению тока короткого замыкания. Очевидно, что ток возбу­ждения по спрямленной характеристике холостого хода отно­сится к насыщенному значению как

.

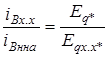При E_q*=1 ОКЗ насыщенной машины равно

OK3_нac = k/x_d*.

Коэффициент k показывает, во сколько раз эдс холостого хода, взятая по спрямленной характеристике, при возбуждении, равном единице, отличается от эдс, определяемой по действи­тельной характеристике холостого хода.

Для турбогенераторов можно принять k=1,2. Таким обра­зом, для определения тока установившегося режима при к. з. на зажимах генератора достаточно знать ОКЗ генератора и ток возбуждения до момента образования к. з. Этот ток возбуждения в относительных единицах можно найти по формуле

,

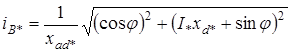где

;

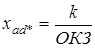cosφ – коэффициент мощности;

I_* - относительный ток статора до режима к.з.

В практических расчетах часто бывает необходимо опреде­лить начальное значение тока к. з. Для решения этой задачи найдем такую эдс, которая имеет в начальный момент то же значение, что и до режима к. з. Внезапное появление вынужден­ной составляющей тока статора вызывает в обмотке возбуждения соответствующий ток, препятствующий изменению потокосцепления этой обмотки в начальный момент к. з. Это приводит к скачку эдс холостого хода генератора до значения E_qк.з0 (см. рис. 22.3). Такие условия работы машины в начальный момент к. з. позволяют рассматривать синхронный генератор как трансформатор с воздушным зазором и воспользоваться его эквивалентной схемой.

Ток возбуждения i_B генератора при холостом ходе создает потокосцепление обмотки возбуждения, которое определяется двумя потоками: полезным ψ_d и рассеяния обмотки возбуждения ψ_sB.

В приведенных к одним условиям относительных единицах потоксцепление равно соответствующему потоку.

Заметим далее, что для удобства записи выражений потокосцеплений машины следует различать токи генератора и нагрузки. В принятой системе координат, связанной с магнитной системой ротора, переменные I, U, Е и т. д. равны амплитудным значениям соответствующих фазных переменных и в установившихся режи­мах представляют собой постоянные векторы в прямоугольной системе координат d, q. Если рассматривать зажимы машины как узловую точку элементарной электрической цепи генератор - нагрузка, то вектор тока нагрузки следует направить от этой узловой точки, тогда как вектор тока генератора - в сторону узловой точки. Таким образом, при положительных значениях
проекций вектора тока нагрузки соответствующие проекции век­тора тока генератора будут отрицательны. Другими словами, справедливо соотношение

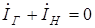или .

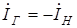При рассмотрении, например, режимов короткого замыкания ток I_d генератора будет отрицательным, что соответствует разма­гничивающему действию реакции статора (индуктивная нагрузка). При емкостной нагрузке он становится положительным. Вслед­ствие этого в уравнениях потокосцеплений следует учитывать во всех случаях алгебраическую сумму составляющих от токов возбуждения и статора, имея в виду, что в процессе вычислений знаки токов будут определяться автоматически.

Потокосцепление обмотки статора в системе осей d, q представ­ляет собой вектор, не совпадающий в общем случае с осью d. Однако при анализе режимов, близких к глухим коротким замы­каниям, можно ограничиться рассмотрением лишь его продольной составляющей, которая образована взаимодействием тока воз­буждения и продольной составляющей тока статора. Учитывая, что в о. е. взаимоиндукция и индуктивность равны соответствую­щим реактивным сопротивлениям, проекцию вектора потокосцепления обмотки статора представим в виде

ψ_d=(x_s+x_ad)I_d+x_adI_B, (22.8)

где x_s + x_ad = x_d.

Таким образом, синхронное реактивное сопротивление в о.е. численно равно индуктивности обмотки статора, которая ма­гнитно связана с контуром обмотки возбуждения, и степень этой связи выражается коэффициентом взаимоиндукции x_ad. Из приведенного выражения видно, что часть потокосцепления статорной обмотки I_dx_s образует поток рассеяния, величина кото­рого пропорциональна реактивному сопротивлению рассеяния статорной обмотки x_s.

Потокосцепление обмотки возбуждения образуется вследствие взаимодействия тех же токов, однако часть его идет на создание потока рассеяния главных полюсов, пропорционального реактив­ности рассеяния обмотки возбуждения x_sb:

ψ_B=(x_sB+x_ad)i_B+x_adI_d. (22.9)

Продольная составляющая потокосцепления обмотки статора создает соответствующую составляющую вектора напряжения, которая отстает на 90°, совпадая с осью q, поэтому при угловой скорости ротора, равной w, получим

ψ_dw=(x_dI_d+x_adi_B)w=U_q. (22.10)

При внезапном изменении режима потокосцепление обмотки возбуждения остается неизменным.

При постоянных значениях x_sB и x_ad постоянство потокосцепления обмотки возбуждения вызывает соответствующее измене­ние тока i_В при изменении тока статора I_d. Это в свою очередь приводит к соответствующему изменению составляющих потокосцепления статора, определяющих напряжение на зажимах ге­нератора.

Чтобы установить взаимосвязь между указанными величи­нами, найдем из выражения (22.9) ток возбуждения i_B и подставим его значение в выражение (22.10), тогда

;

.

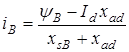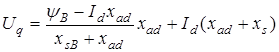После несложных преобразований последнее выражение при­мет вид

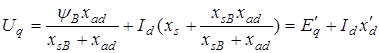, (22.11)

т. е. напряжение на зажимах генератора равно некоторой эдс 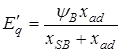минус падение напряжения в реактивном сопротивлении x'_d при токе I_d (в данном режиме I_d < 0).

Эти величины определялись из условия постоянства потокосцепления обмотки возбуждения в начальный момент режима к. з. Из сказанного следует, что именно эти величины можно брать как расчетные при определении начального тока к. з. Электродвижущая сила синхронного генератора E'_q и его реактивное сопротивление x'_d, определяемые по указанным условиям, назы­ваются переходными параметрами генератора.

Если синхронный генератор имеет успокоительные обмотки, то его эдс и сопротивление с учетом влияния этих обмоток называются сверхпереходными па­раметрами и обозначаются соответственно E''_q и x''_d.

Таким образом, зная условия работы генератора до начала к. з., можно найти значение переходной эдс

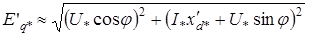, (22.12)

которое остается неизменным и в начальный момент возникнове­ния к. з.

По соотношению

(22.13)

определяется начальный ток к. з. генератора в переходном ре­жиме.

Переходное реактивное сопротивление генератора приводится в каталогах и справочниках.

Определение токов к.з. без успокоительных обмоток

На рис. 22.5 приведена эквивалентная схема замещения синхронного генератора в переходном режиме.

Принимая обмотку статора за основную и рассматривая об­мотку возбуждения как короткозамкнутую, можно найти переход­ное реактивное сопротивление генератора:

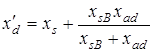
Такое же выражение для x'_d было получено ранее (см. (22.11).

При определении постоянной времени затухания токов переходного режима за основную следует принимать обмотку возбуждения, поскольку изменение тока возбуждения определяет изменение эдс генератора, а значит, и тока статора. В данном случае реактивное сопротивление машины, определяющее постоянную времени затухания переходного тока, равно

.

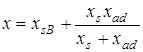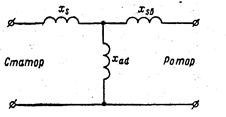
Рис. 22.5. Эквивалентная схема замещения генератора

В соответствии с этим постоянная времени затухания переход­ного тока составит

.

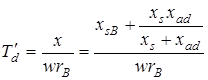Полученное выражение после некоторых преобразований примет вид

,

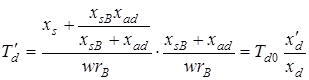где 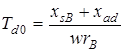- постоянная времени затухания токов обмотки ротора при разомкнутой обмотке статора. Обычно значение T_d0 приводится в каталогах и справочниках.

Выше отмечалось, что периодический ток к. з. в любой момент аварийного режима генератора без успокоительных обмоток можно найти по выражению

.

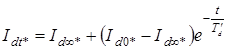При этом в данное выражение следует подставить значение установившегося тока к.з., которое можно определить по соотношению (22.7), и начальный ток, найденный по выражению (22.13),

.