Определение координат нескольких точек
Задача Ганзена
В задаче Ганзена находят координаты двух точек P и Q по известным координатам двух пунктов A и B и четырем углам, измеренным на определяемых точках (рис.2.15), то-есть, задача Ганзена является сдвоенной обратной угловой засечкой.
Исходные данные: XA, YA, XB, YB.
Измеренные элементы: β1, β2, β3, β4.
Неизвестные элементы: XP, YP, XQ, YQ.
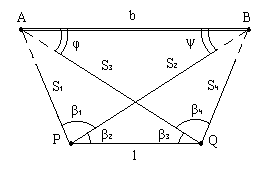
Рис.2.15. Схема задачи Ганзена
Графическое решение. Взять два листа прозрачной бумаги (кальки) и построить на них углы: на одном листе - углы β1 и β2, на другом листе - углы β3 и β4. Наложить на чертеж (план или карту) оба листа и, перемещая их произвольным образом, совместить направления углов на этих листах с точками А и В на чертеже. Переколоть точки P и Q на чертеж.
Аналитическое решение. Известно несколько способов решения задачи Ганзена; приведем краткое изложение одного из них.
Решить обратную задачу между пунктами A и B, то-есть, вычислить длину b отрезка AB и дирекционный угол αAB направления AB.
Ввести условную единицу длины, равную длине l отрезка PQ; l = 1.000 .
Вычислить отрезки S'1 = AP, S'3 = AQ, S'2 = BP, S'4 = BQ в условных единицах с использованием теоремы синусов сначала для треугольника PAQ, затем для треугольника PBQ:
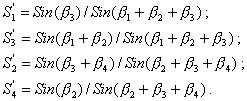 (2.55)
(2.55)
Вычислить в условных единицах длину b' отрезка AB из треугольника QAB по теореме косинусов:
 (2.56)
(2.56)
и для контроля - из треугольника PAB:
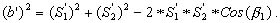 (2.57)
(2.57)
Оба значения должны совпасть.
Вычислить масштабный коэффициент k:
k = b / b' (2.58)
и перевести все вычисленные расстояния в реальные единицы длины:
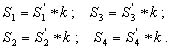 (2.59)
(2.59)
Вычислить угол φ из треугольника QAB по теореме косинусов:
 (2.60)
(2.60)
Вычислить угол ψ из треугольника PAB по теореме косинусов:
 (2.61)
(2.61)
Вычислить дирекционный угол направления AQ:
 (2.62)
(2.62)
и решить прямую геодезическую задачу с пункта A на точку Q :
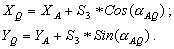 (2.63)
(2.63)
Вычислить дирекционный угол направления BP αBP= αBA - φ и решить прямую геодезическую задачу с пункта B на точку P:

Расположение исходных пунктов и определяемых точек может быть таким, что отрезки PQ и AB будут пересекаться (рис.2.16); ход решения задачи остается таким же, только изменятся обозначения углов и сторон. Кроме того, доказано, что в этом варианте положение точек P и Q определяется в несколько раз точнее, чем в общем варианте.
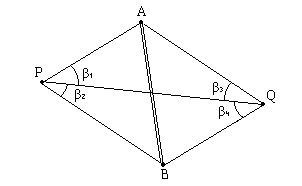
Рис.2.16. Вариант задачи Ганзена
В однократной задаче Ганзена отсутствует контроль измерений, поэтому на практике четырьмя измерениями углов не ограничиваются, а выполняют какие-либо дополнительные измерения.
Дата добавления: 2016-02-02; просмотров: 786;
